Calculating Acceleration from Speed-Time Graphs

Interpreting speed-time graphs

Extended tier only

When interpreting speed-time graphs, the shape of the graph can show:
- constant acceleration
- changing acceleration

The gradient of a speed-time graph shows the acceleration of a moving object
- The gradient is positive if the object is accelerating (speed increases with time)
- The gradient is negative if the object is decelerating (speed decreases with time)

Interpreting constant positive acceleration on a speed-time graph

When the acceleration is constant and non-zero:
- the graph is a straight line
- velocity is increasing at a constant rate, i.e. speed changes by the same amount in equal intervals of time

Constant positive acceleration on a speed-time graph

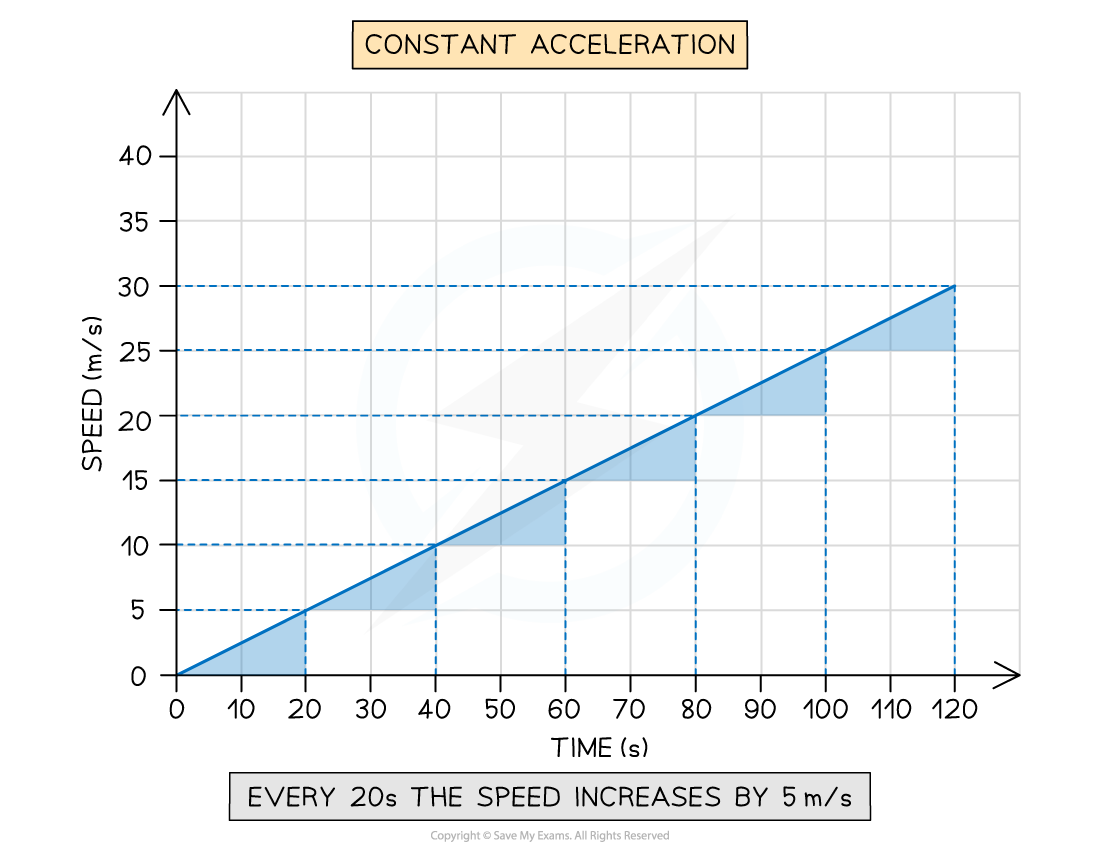
cie-1-2-5-constant-acceleration-graph

A speed-time graph for an object with constant positive acceleration. Its speed increases by 5 m/s every 20 s, showing that the rate at which the speed increases is constant.

Interpreting increasing positive acceleration on a speed-time graph

When the acceleration is increasing:
- the graph is a curve
- velocity is increasing at an increasing rate, i.e. the speed changes by the same amount in increasingly shorter time intervals

Increasing positive acceleration on a speed-time graph

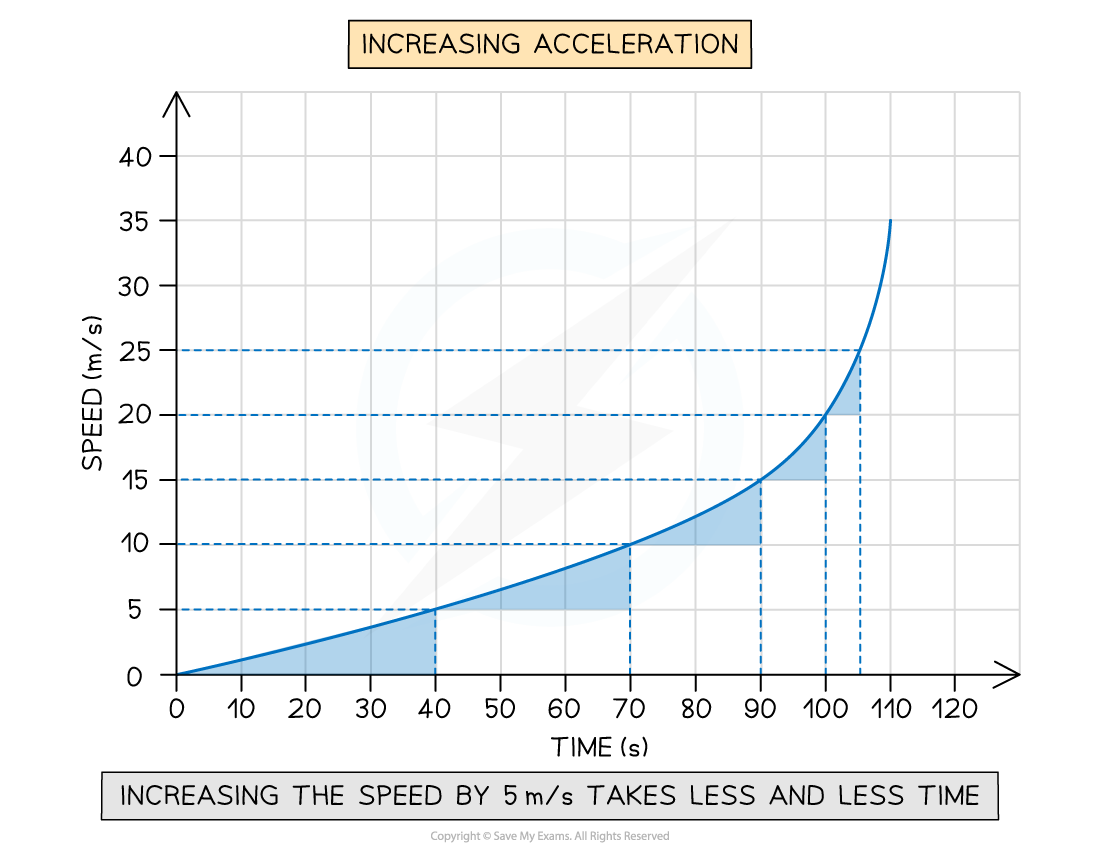
cie-1-2-5-increasing-acceleration-graph

A speed-time graph for an object with changing positive acceleration. The time taken for the speed to increase by 5 m/s decreases over time, showing that acceleration is increasing.

Interpreting decreasing positive acceleration on a speed-time graph

When the acceleration is decreasing:
- the graph is a curve
- velocity is increasing at a decreasing rate, i.e. the speed changes by the same amount in increasingly longer time intervals

Decreasing positive acceleration on a speed-time graph

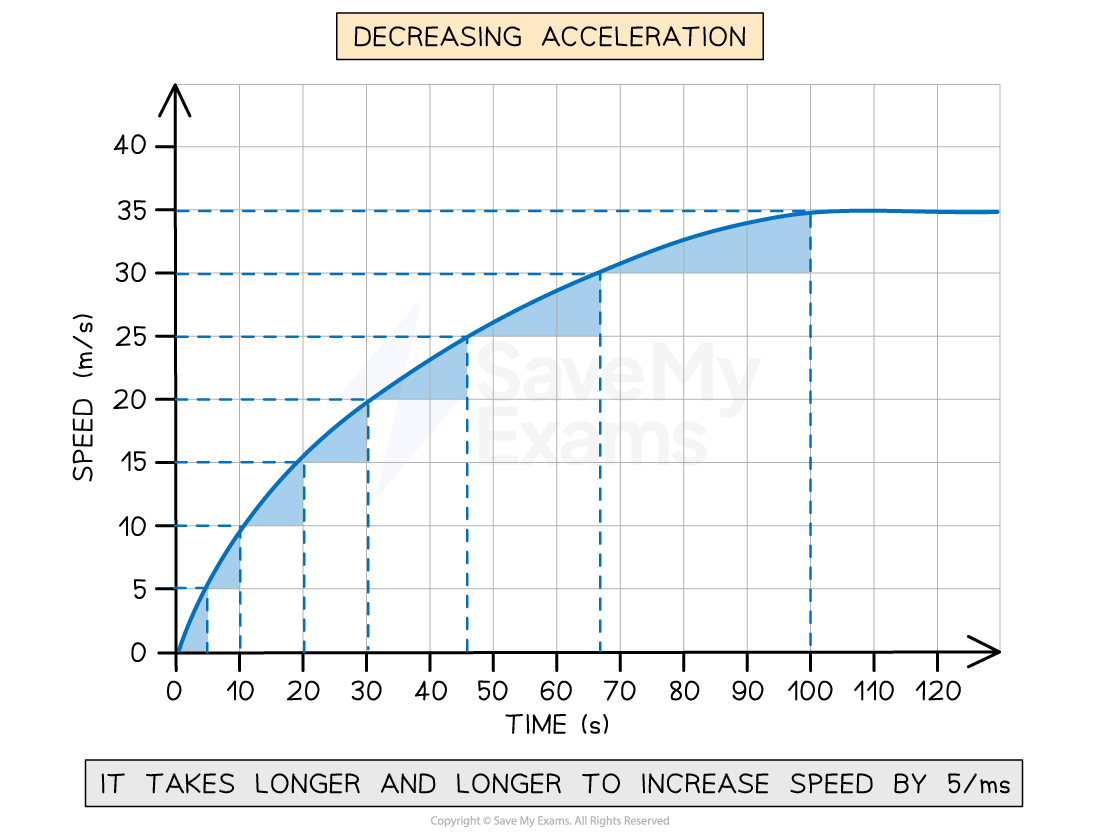
A speed-time graph for an object with changing positive acceleration. The time taken for the speed to increase by 5 m/s increases over time, showing that acceleration is decreasing.

Interpreting decreasing negative acceleration on a speed-time graph

When the deceleration is decreasing:
- the graph is a curve
- the velocity is decreasing at a decreasing rate, i.e. the speed changes by the same amount in increasingly longer intervals of time

Decreasing negative acceleration on a speed-time graph

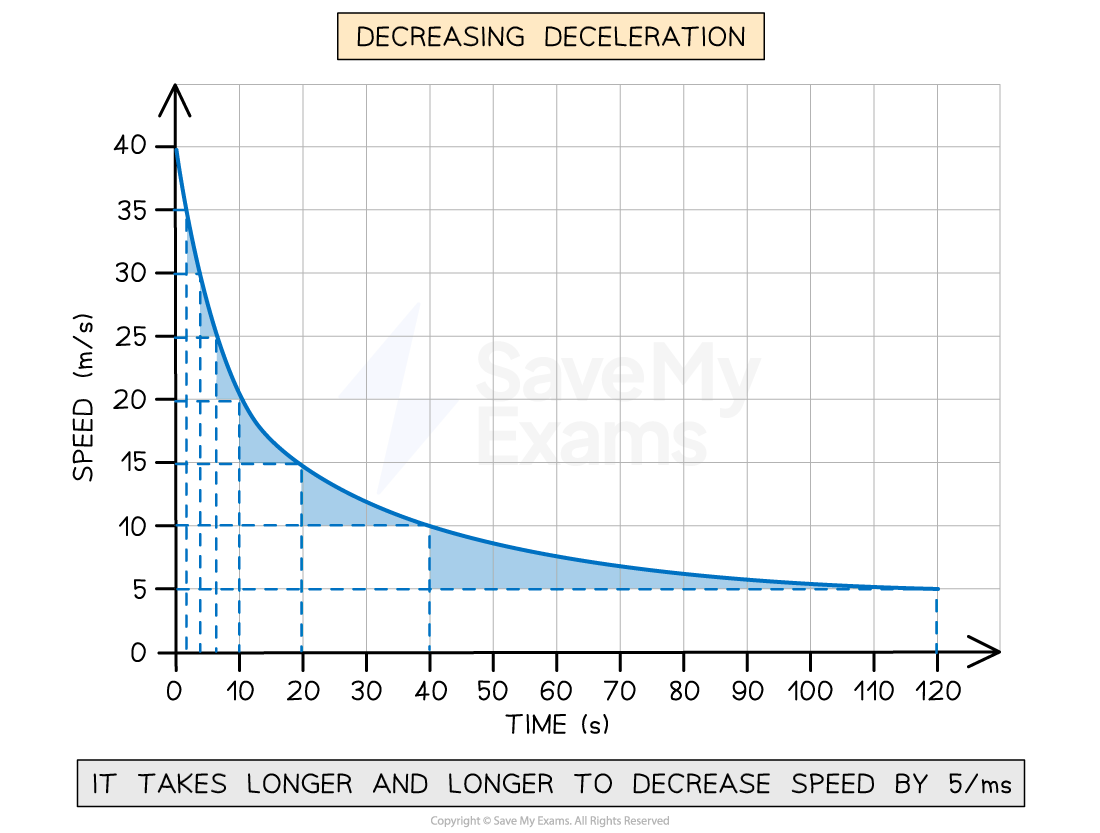
new-1-2-5-decreasing-deceleration

A speed-time graph for an object with changing negative acceleration. The time taken for the speed to decrease by 5 m/s increases over time, showing that deceleration is decreasing.

Examiner Tip

Interpreting graphs can be difficult, and students often struggle with this key skill

In CIE IGCSE Physics, interpreting graphs is a required skill

For your exam, you are also expected to calculate the gradient of a graph and the area under a graph
Finding the area under a graph is covered in the revision note Speed-time graphs

Extended tier only

The acceleration of an object can be calculated from the gradient of a speed-time graph

Finding the gradient when acceleration is constant

When acceleration is constant, the speed-time graph will be a straight line
The gradient of a straight line can be found using:

$gradient = \frac{∆ y}{∆ x}$

Where:
- $∆ y$ = change in $y$ (speed) values
- $∆ x$ = change in $x$ (time) values

Therefore, the gradient is equal to:

$a = \frac{∆ v}{∆ t}$

Where:
- $a$ = acceleration, measured in metres per second squared (m/s²)
- $∆ v$ = change in speed, measured in metres per second (m/s)
- $∆ t$ = change in time, measured in seconds (s)

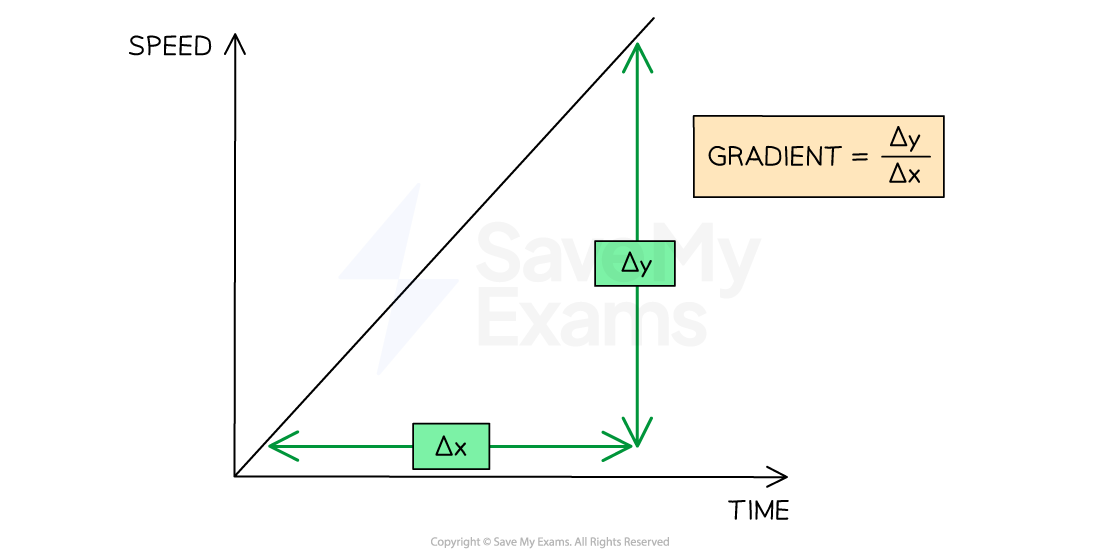
gradient-speed-time-graphs

The gradient of a speed-time graph for constant acceleration can be found using Δy divided by Δx

Finding the gradient when acceleration is changing

When acceleration is changing, the speed-time graph will be a curve
The gradient of a point on a curve can be found by drawing a tangent to the curve

A tangent to the curve

2-3-properties-of-motion-graphs-tangent-to-a-curve_edexcel-al-physics-rn

The value of the gradient at a single point on a curve can be determined by finding the gradient of the tangent to that point

The tangent provides a gradient that is representative of the gradient at a specific point on the curve
The gradient of the tangent can be found using:

$gradient = \frac{∆ y}{∆ x}$

The value of the gradient at specific point on the curve represents the acceleration of the object at that moment
- This is called instantaneous acceleration

Worked example

A cyclist is training for a cycling tournament.

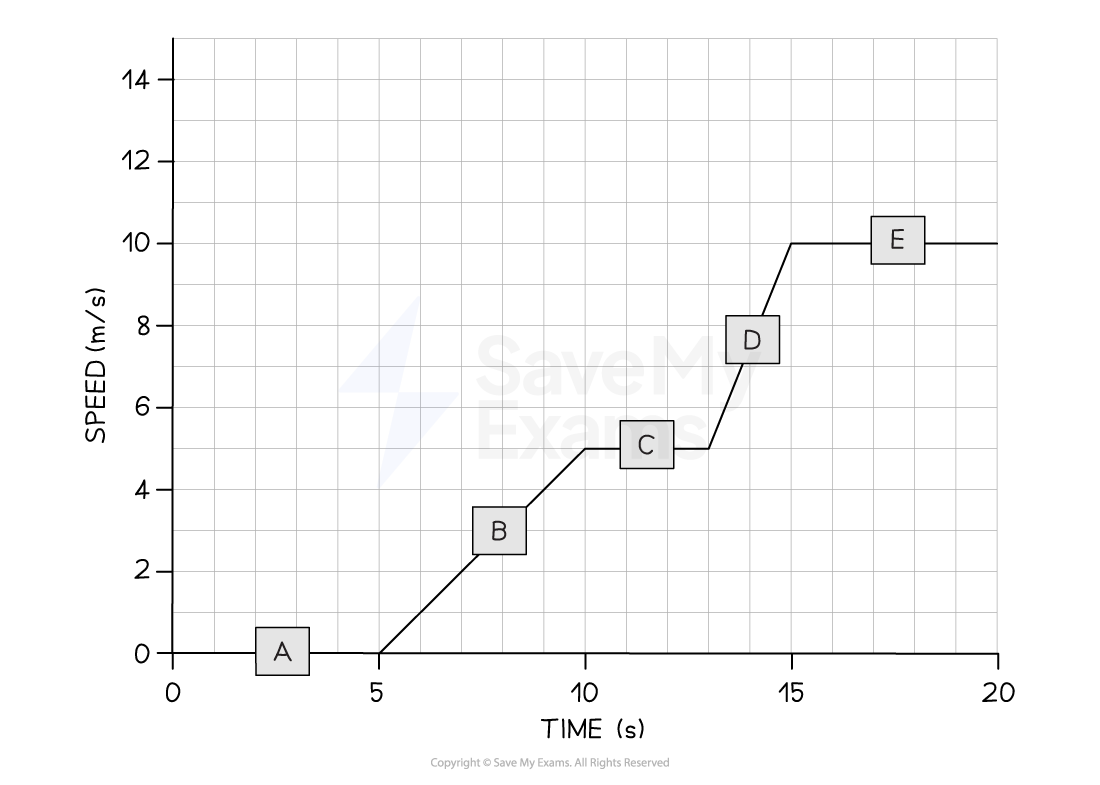
The speed-time graph below shows the cyclist's motion as they cycle along a flat, straight road. speed-time-gradient-we1

(a) In which section (A, B, C, D, or E) of the speed-time graph is the cyclist's acceleration the largest?

(b) Calculate the cyclist's acceleration between 5 and 10 seconds.

Answer:

Part (a)

Step 1: Recall that the slope of a speed-time graph represents the magnitude of acceleration

The slope of a speed-time graph indicates the magnitude of acceleration
Therefore, the only sections of the graph where the cyclist is accelerating are sections B and D
Sections A, C, and E are flat; in other words, the cyclist is moving at a constant velocity (therefore, not accelerating)

Step 2: Identify the section with the steepest slope

Section D of the graph has the steepest slope
Hence, the largest acceleration is shown in section D

Part (b)

Step 1: Recall that the gradient of a speed-time graph gives the acceleration

Calculating the gradient of a slope on a speed-time graph gives the acceleration for that time period

Step 2: Draw a large gradient triangle at the appropriate section of the graph

A gradient triangle is drawn for the time period between 5 and 10 seconds

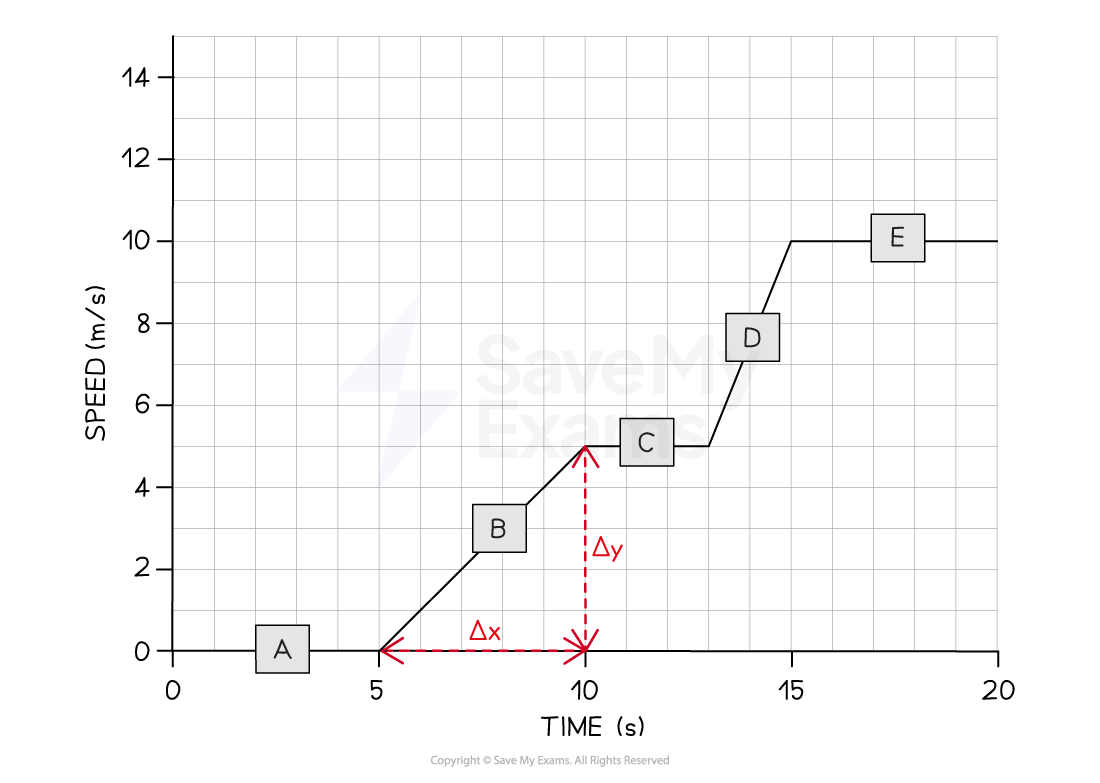
speed-time-gradient-we2

Step 3: Calculate the size of the gradient and state this as the acceleration

The acceleration is given by the gradient, which can be calculated using:

$a = \frac{∆ y}{∆ x}$

$a = \frac{5}{5}$

$a = 1 m / s^{2}$

Therefore, the cyclist accelerated at 1 m/s² between 5 and 10 seconds

Examiner Tip

Use the entire slope, where possible, to calculate the gradient. Examiners tend to award credit if they see a large gradient triangle used.

Remember to actually draw the lines directly on the graph itself, particularly when the question asks you to use the graph to calculate the acceleration.

Worked example

A skydiver jumps from a plane and reaches terminal velocity after 15 seconds. A speed-time graph of their motion is shown below.

Use the graph to find the acceleration at 5 seconds.

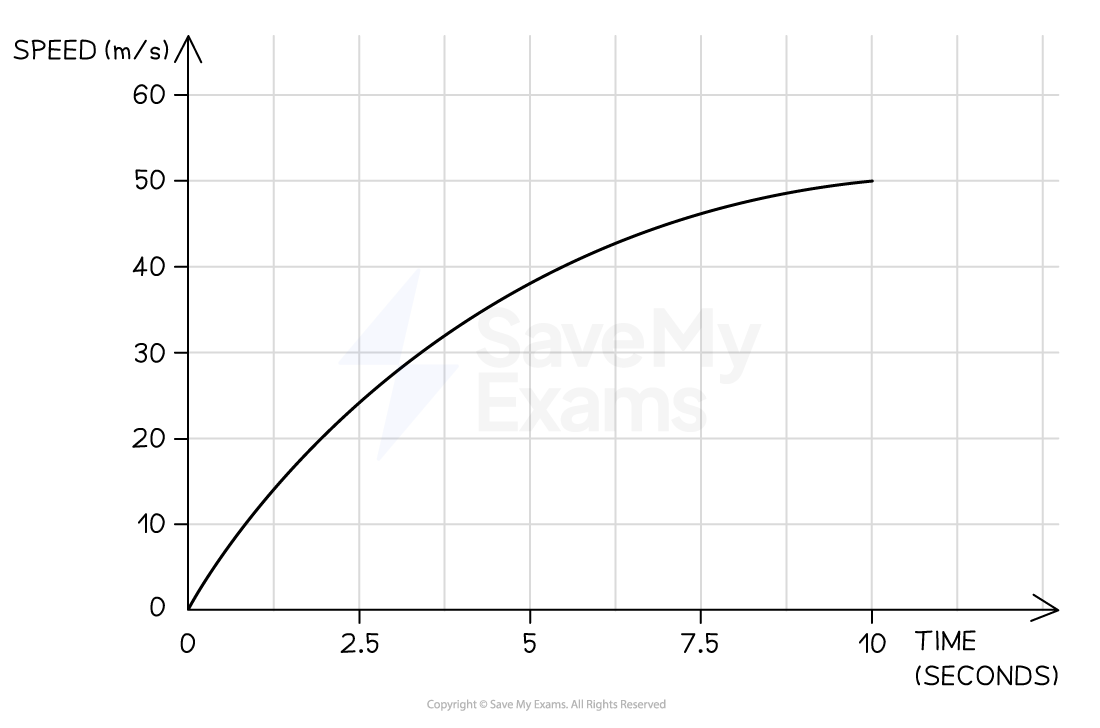
speed-time-curve-we

Answer:

Step 1: Draw a tangent to the curve at the point where t = 5 s

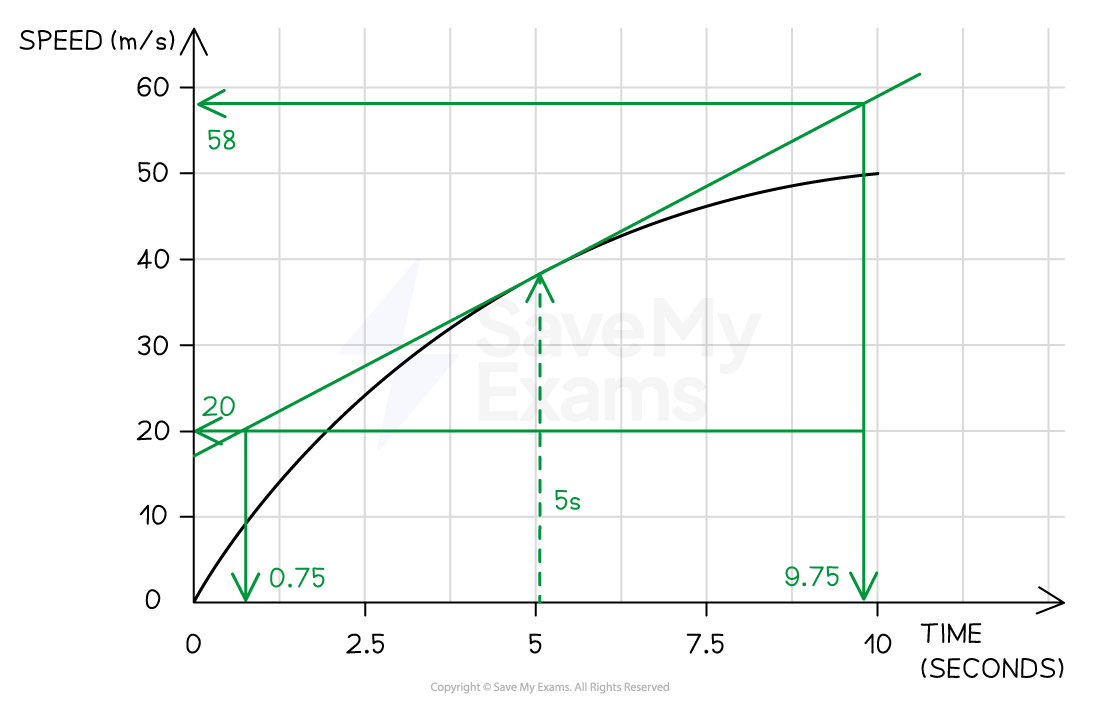
Step 2: Calculate the gradient of the tangent

$a = \frac{∆ y}{∆ x}$

$a = \frac{58 - 20}{9.75 - 0.75}$

$a = \frac{38}{9.0}$

$a = 4.2 m / s^{2} (2 s . f .)$

Examiner Tip

The CIE IGCSE Co-ordinated Sciences specification includes knowing how to calculate the gradient of a tangent to the curve in the maths skills section. This means that you could be asked to demonstrate this skill in any topic. The skills in this revision note are applicable to any type of graph. For more information on interpreting graphs in Physics, see the article Graph skills in GCSE Physics

Calculating Acceleration from Speed-Time Graphs (CIE IGCSE Physics: Co-ordinated Sciences (Double Award))

Revision Note

Interpreting speed-time graphs

Interpreting constant positive acceleration on a speed-time graph

Constant positive acceleration on a speed-time graph

Interpreting increasing positive acceleration on a speed-time graph

Increasing positive acceleration on a speed-time graph

Interpreting decreasing positive acceleration on a speed-time graph

Decreasing positive acceleration on a speed-time graph

Interpreting decreasing negative acceleration on a speed-time graph

Decreasing negative acceleration on a speed-time graph

Examiner Tip