IGCSEPhysicsOxford AQARevision NotesWavesRefraction & Total Internal ReflectionTotal Internal Reflection

Total Internal Reflection (Oxford AQA IGCSE Physics)

Revision Note

Ann Howell

Written by: Ann Howell

Reviewed by: Caroline Carroll

Critical Angle

  • The relationship between refractive index, n, and critical angle, c, is:

n space equals space fraction numerator 1 over denominator sin space c end fraction

  • The equation can be rearranged to make sin c the subject:

sin space c space equals space 1 over n

  • The larger the refractive index of a material, the smaller the critical angle

  • When light is shone at the boundary between a more dense and a less dense medium, different angles of incidence result in different angles of refraction

    • As the angle of incidence is increased, the angle of refraction also increases

    • Until the angle of incidence reaches the critical angle

  • When the angle of incidence = critical angle then:

    • Angle of refraction = 90°

    • The refracted ray is refracted along the boundary between the two materials

  • When the angle of incidence < critical angle then:

    • the ray is refracted and exits the material

  • When the angle of incidence > critical angle then:

    • the ray undergoes total internal reflection

Angle of refraction, critical angle and reflection

Different angles of incidence give different angles of refraction and reflection depending on the refractive index
As the angle of incidence increases it will eventually exceed the critical angle and lead to the total internal reflection of the light

Worked Example

Opals and diamonds are transparent stones used in jewellery. Jewellers shape the stones so that light is reflected inside.

Compare the critical angles of opal and diamond and explain which stone would appear to sparkle more.

The refractive index of opal is about 1.5

The refractive index of diamond is about 2.4

Answer:

Step 1: List the known quantities

  • Refractive index of opal, no = 1.5

  • Refractive index of diamond, nd = 2.4

Step 2: Write out the equation relating critical angle and refractive index

sin space c space equals space 1 over n

Step 3: Calculate the critical angle of opal (co)

sin space c subscript 0 space equals space 1 over n subscript o

sin space c subscript 0 space equals space fraction numerator 1 over denominator 1.5 end fraction

sin space c subscript 0 space equals space 0.6667

c subscript o space equals space sin to the power of negative 1 end exponent open parentheses 0.6667 close parentheses space

c subscript o equals space 42 degree space open parentheses 2 space straight s. straight f. close parentheses

Step 4: Calculate the critical angle of diamond (cd)

sin space c subscript d space equals space 1 over n subscript d

sin space c subscript d space equals space fraction numerator 1 over denominator 2.4 end fraction space

sin space c subscript d space equals space 0.4167

c subscript d space equals space sin to the power of negative 1 end exponent space open parentheses 0.4167 close parentheses space

c subscript d space equals space space 25 degree space open parentheses 2 space straight s. straight f. close parentheses

Step 5: Compare the two values and write a conclusion

  • Total internal reflection occurs when the angle of incidence of light is larger than the critical angle (i>c)

  • In opal, total internal reflection will occur for angles of incidence between 42° and 90°

  • The critical angle of diamond is lower than the critical angle of opal (co>cd)

  • This means light rays will be totally internally reflected in diamond over a larger range of angles (25° to 90°)

  • Therefore, more total internal reflection will occur in the diamond, hence it will appear to sparkle more than the opal

Examiner Tips and Tricks

In your exam, you are not required to recall the values of critical angles for different materials.

When calculating the value of the critical angle using the above equation:

  • First use the refractive index, n, to find sin(c)

  • Then use the inverse sine function (sin–1) to find the value of c

Total Internal Reflection

  • Total internal reflection is a special case of refraction that occurs when:

    • The angle of incidence within the denser medium is greater than the critical angle

  • Total internal reflection follows the law of reflection

angle of incidence = angle of reflection

  • A denser medium has a higher refractive index

    • For example, the refractive index of glass, ng > the refractive index of air, na

  • Light rays inside a material with a higher refractive index are more likely to be totally internally reflected

Worked Example

A glass cube is held in contact with a liquid and a light ray is directed at a vertical face of the cube. The angle of incidence at the vertical face is 39° and the angle of refraction is 25° as shown in the diagram. The light ray is totally internally reflected for the first time at X.

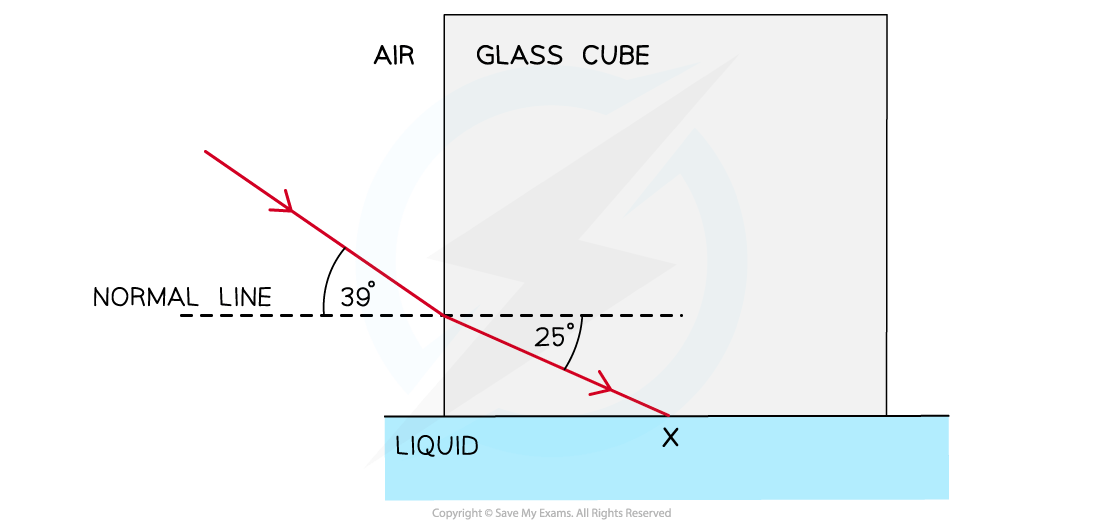
A glass cube sits on top of a liquid. A light ray enters the glass cube from the left-hand side, with an angle of incidence equal to 39 degrees. The light ray is refracted at the air to glass boundary with an angle of refraction equal to 25 degrees. The light ray hits the glass to liquid boundary at the centre point which is labelled X

Complete the diagram to show the path of the ray beyond X to the air.

You should include the values of any angles you draw.

Answer:

A normal is drawn at point X. The light ray is totally internally reflected at the glass to liquid boundary. The angle of reflection is 65 degrees, equal to the angle of incidence. The light ray hits the glass to air boundary on the right hand side of the glass cube at an angle of incidence equal to 25 degrees. The light ray enters the air with an angle of refraction equal to 39 degrees.

Step 1: Draw the reflected ray at the glass-liquid boundary

  • When a light ray is reflected, the angle of incidence = angle of reflection

  • Therefore, the angle of incidence (or reflection) is 90° – 25° = 65°

  • First, draw in the normal as a dotted line

  • Then draw in the reflected ray at an angle of 65° from the normal

Step 2: Draw the refracted angle at the glass-air boundary

  • At the glass-air boundary, the light ray refracts away from the normal

  • Due to the reflection occurring at the exact centre point of the glass block, the light rays are symmetrical on both sides

Uses of Total Internal Reflection

  • Visible light and infrared can be transmitted through optical fibres by total internal reflection

Total internal reflection in an optical fibre

A light ray travelling through a glass optical fibre is reflected from the edge of the fibre back into it. This is how it travels all the way along.
Optical fibres utilise total internal reflection for communications

  • In an optical fibre, the denser medium is the glass that forms the fibre

    • The air outside the fibre is the less dense medium

Optical fibres in medicine

  • Optical fibres are used in medicine to see within the human body

  • An endoscopy is a medical procedure that uses an endoscope to look inside the body

  • An endoscope contains a camera on a long, thin flexible tube containing an optical fibre 

    • It can be used to obtain images of the digestive tract by insertion of the endoscope

  • Endoscopes allow doctors to:

    • Identify the exact location of a problem

    • Suggest the correct treatment

    • Treat a patient more quickly

    • Provide more effective medicine

An endoscope

Endoscope, for IGCSE & GCSE Physics revision notes
Endoscopes utilise total internal reflection to see inside a patient's body

Optical fibres in communication

  • Optical fibres can be used to transmit:

    • Landline telephone signals

    • Internet signals

    • Cable television signals

  • In these systems, electrical signals are converted to light pulses that travel at high speeds along the optical fibre

    • Slower systems still use the old copper cables for some sections of the transmission

  • Optical fibres have many advantages over copper cables:

    • They use less energy to transmit the signal

    • They need fewer boosters to increase the signal

    • There is no interference with nearby cables

    • They are difficult to intercept

    • Their mass is lower, so they are easier to install

Fibre optic and copper cables

On the left shows the inside of a fibre optic cable. On the right shows the inside of a copper cable.
Copper cables are heavier and more difficult to install than fibre optic cables

Last updated:

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Did this page help you?

    Previous:Investigating the Refraction of LightNext:Lenses
    Author
    Reviewer
    Ann Howell

    Author: Ann Howell

    Expertise: Physics Content Creator

    Ann obtained her Maths and Physics degree from the University of Bath before completing her PGCE in Science and Maths teaching. She spent ten years teaching Maths and Physics to wonderful students from all around the world whilst living in China, Ethiopia and Nepal. Now based in beautiful Devon she is thrilled to be creating awesome Physics resources to make Physics more accessible and understandable for all students, no matter their schooling or background.

    Caroline Carroll

    Author: Caroline Carroll

    Expertise: Physics Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.