Velocity-Time Graphs (Oxford AQA IGCSE Physics)

Revision Note

Written by: Leander Oates

Reviewed by: Caroline Carroll

Calculating Acceleration from a Velocity-Time Graph

The gradient of the line on a velocity-time graph represents the magnitude of acceleration
- A steep gradient means large acceleration (or deceleration)
  - The object's velocity changes very quickly
- A gentle gradient means small acceleration (or deceleration)
  - The object's velocity changes very gradually
- A horizontal line means the acceleration is zero
  - The object is moving with a constant velocity
  - A constant velocity means a constant speed in a straight line
  - A horizontal line at v = 0 shows a stationary object

Interpreting gradients on a Velocity-Time graphs

Different gradients on a velocity-time graph for IGCSE & GCSE Physics revision notes — **This image shows how to interpret the gradients of a velocity-time graph**

The acceleration of an object can be calculated from the gradient of a velocity-time graph

$acceleration = gradient = \frac{∆ y}{∆ x}$

Here, Δy is change in velocity and Δx is change in time

Calculating the gradient of a Velocity-Time graph

Annotated velocity-time graph for IGCSE & GCSE Physics revision notes — **To find the gradient, you calculate ∆y, the change in velocity, over ∆x, the change in time**

Worked Example

A cyclist is training for a tournament.

The velocity-time graph below shows the cyclist's motion as they cycle along a flat, straight road.

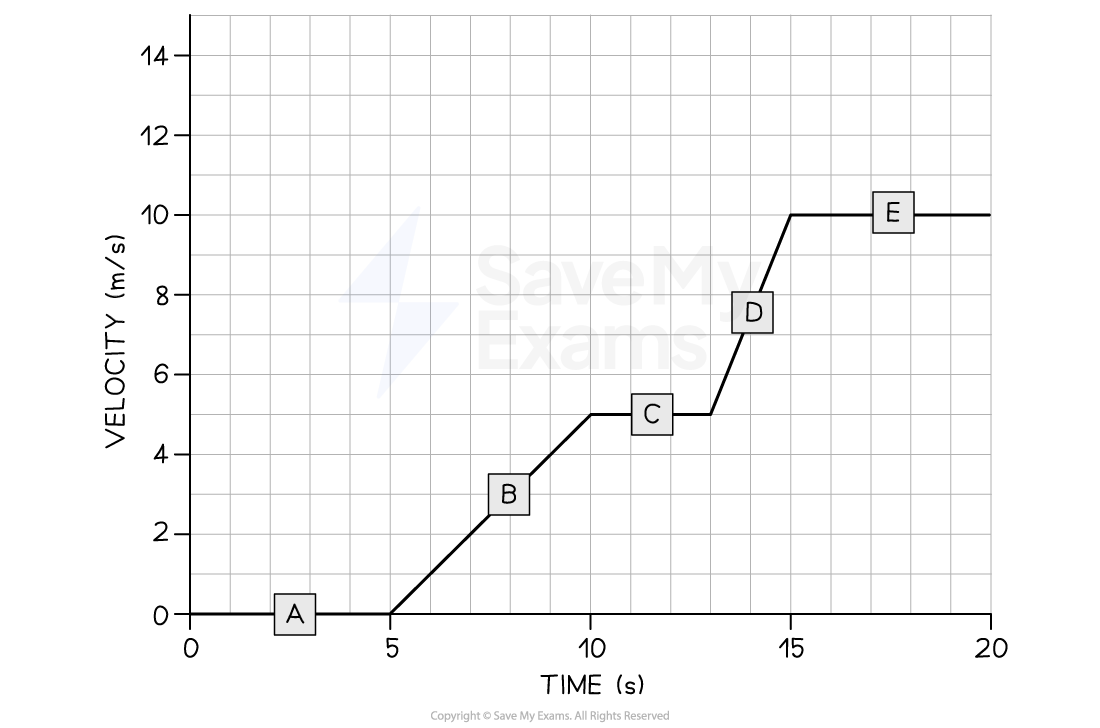
A graph showing five line segments. Segment A is a horizontal line at v=0 between 0 and 5 seconds. Segment B is a straight ascending line as the object's velocity increases from 0 to 5 metres per second between the time interval of 5 to 10 seconds. Segment C is horizontal at v = 5 metres per second from t = 10 seconds to t = 13 seconds. Segment D ascends sharply again as the velocity increases from 5 to 10 metres per second over the time interval between 13 and 15 seconds. Segment E is a horizontal line at v = 10 metres per second from t = 15 seconds to t = 20 seconds

(a) In which section of the velocity-time graph is the cyclist's acceleration the largest?

(b) Calculate the cyclist's acceleration between 5 and 10 seconds.

Answer:

Part (a)

Step 1: Recall what the gradient of a velocity-time graph shows

The gradient of a velocity-time graph indicates the magnitude of acceleration
Therefore, the only sections of the graph where the cyclist is accelerating are section B and section D
Sections A, C, and E are flat – in other words, the cyclist is moving at a constant speed (i.e. not accelerating)

Step 2: Identify the section with the steepest gradient

Section D of the graph has the steepest gradient
Hence, the greatest acceleration is shown in section D

Part (b)

Step 1: Draw a large gradient triangle at the appropriate section of the graph

A gradient triangle is drawn for the time interval between 5 and 10 seconds below:

The graph is annotated with a gradient triangle showing the change in velocity is zero to 5 metres per second for the time interval t = 5 seconds to t = 10 seconds (segment B)

Step 3: Calculate the gradient

$acceleration = gradient = \frac{∆ y}{∆ x}$

$a = \frac{5}{5}$

$a = 1 m / s^{2}$

Therefore, the cyclist accelerated at 1 m/s² between 5 and 10 seconds

Examiner Tips and Tricks

Use the entire gradient line, where possible, to calculate the gradient. Examiners tend to award credit if they see a large gradient triangle used - so remember to draw the lines directly on the graph itself!

Calculating Distance from a Velocity-Time Graph

The distance travelled by an object can be found by determining the area beneath a velocity-time graph

Calculating the area under a Velocity-Time graph

The area under a velocity time graph can be calculated using the area of a triangle for a sloped line and the area of a rectangle for a horizontal line. For IGCSE & GCSE Physics revision notes — **The distance travelled can be found from the area beneath the graph**

If the area beneath the graph forms a triangle (the object is accelerating or decelerating) then the area can be determined using the formula:

$area = \frac{1}{2} \times base \times height$

If the area beneath the graph is a rectangle (constant velocity) then the area can be determined using the formula:

$area = base \times height$

Worked Example

The velocity-time graph below shows a car journey which lasts for 160 seconds.

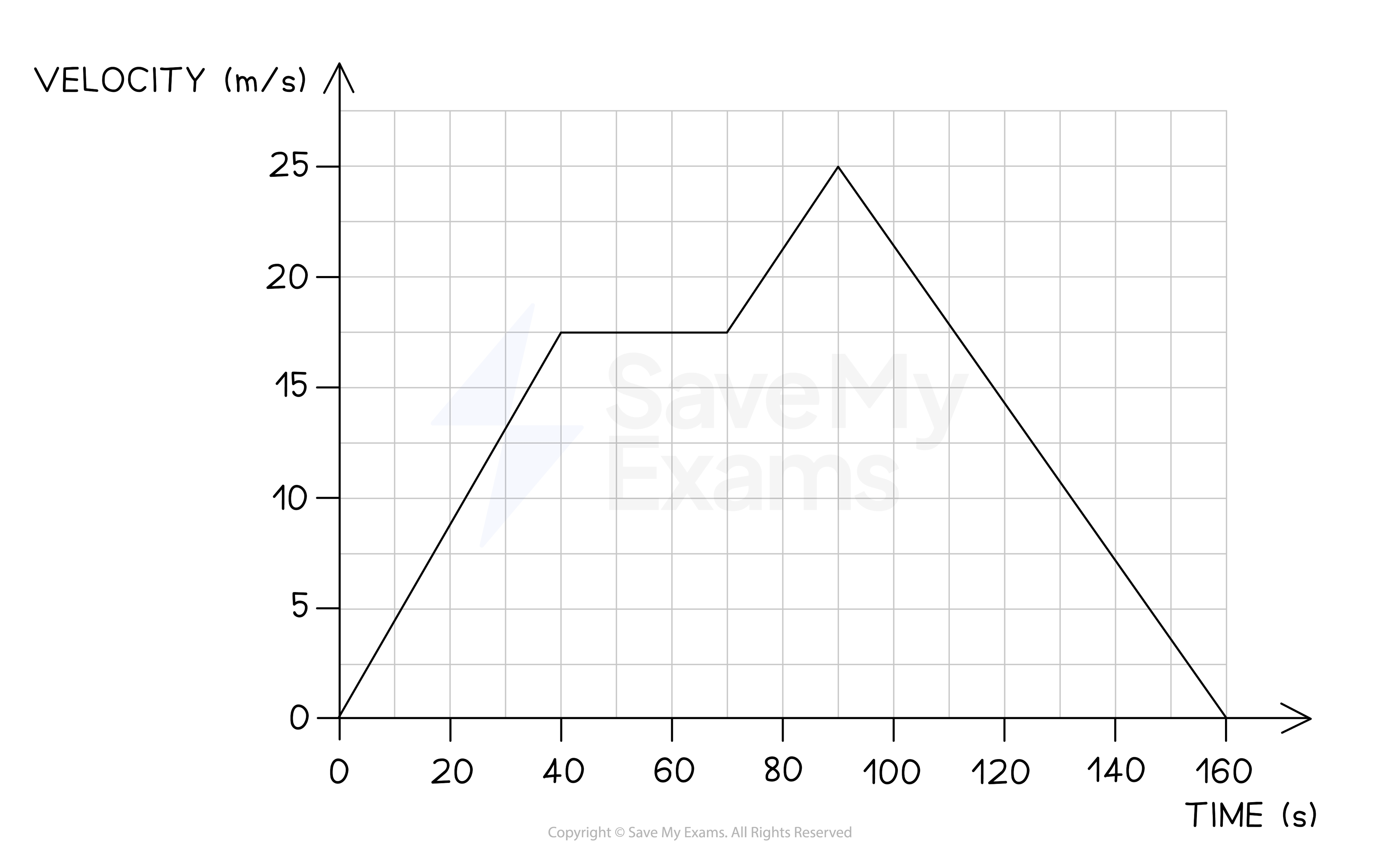
A velocity-time graph with 4 segments. The first segment is an upward sloping line from v = 0 to v = 17.5 metres per second over the time interval t = 0 to t = 40 seconds. The second is a horizontal line at v = 17.5 metres per second for the time interval t = 40 seconds to t = 70 seconds. The third is an upward sloping line from v = 17.5 metres per second to v = 25 metres per second for the time interval t = 70 seconds to t = 90 seconds. The final line segment is a downward sloping line from v = 25 metres per second to v = 0 over the time interval t = 90 seconds to t = 160 seconds.

Calculate the total distance travelled by the car on this journey.

Answer:

Step 1: Recall that the area under a velocity-time graph represents the distance travelled

To calculate the total distance travelled, the total area underneath the line must be determined

Step 2: Identify each enclosed area

In this example, there are five enclosed areas under the line
These can be labelled as areas 1, 2, 3, 4 and 5, as shown in the image below:

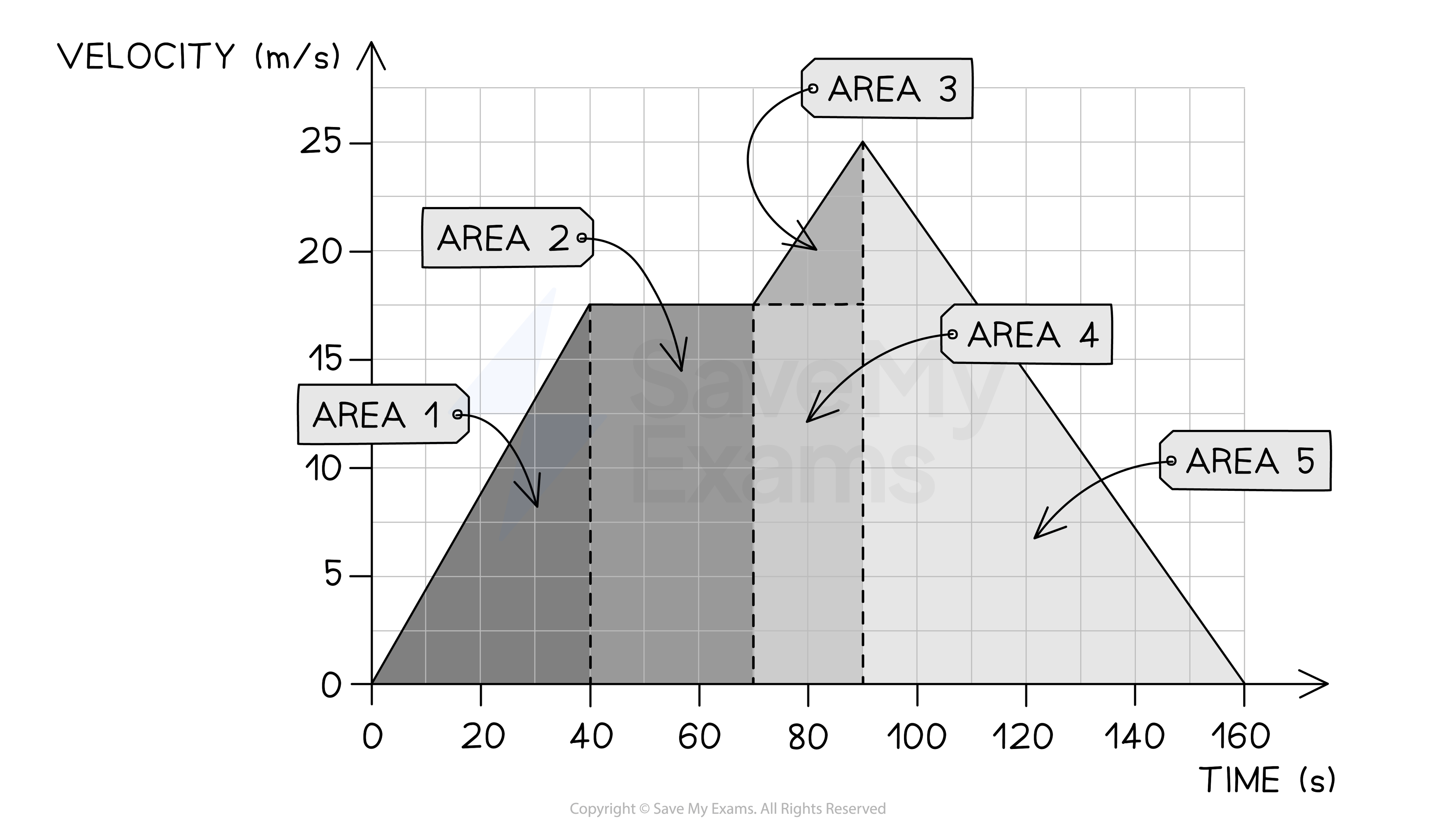
The same graph has been annotated to show area under each line segment in triangles and rectangles. Sloping lines are calculated using triangles and flat lines are calculated using rectangles. However, segment 3's area consists of a rectangle and a triangle on top of it.

Step 3: Calculate the area of each enclosed shape under the line

Area 1 = area of a triangle

$Area 1 = \frac{1}{2} \times base \times height$

$Area 1 = \frac{1}{2} \times 40 \times 17.5$

$Area 1 = 350 m$

Area 2 = area of a rectangle

$Area 2 = base \times height$

$Area 2 = 30 \times 17.5$

$Area 2 = 525 m$

Area 3 = area of a triangle

$Area 3 = \frac{1}{2} \times base \times height$

$Area 3 = \frac{1}{2} \times 20 \times 7.5$

$Area 3 = 75 m$

Area 4 = area of a rectangle

$Area 4 = base \times height$

$Area 4 = 20 \times 17.5$

$Area 4 = 350 m$

Area 5 = area of a triangle

$Area 5 = \frac{1}{2} \times base \times height$

$Area 5 = \frac{1}{2} \times 70 \times 25$

$Area 5 = 875 m$

Step 4: Calculate the total distance travelled by finding the total area under the line

Add up each of the five areas enclosed:

$total distance = Area 1 + Area 2 + Area 3 + Area 4 + Area 5$

$total distance = 350 + 525 + 75 + 350 + 875$

$total distance = 2175 m$

Last updated: 23 April 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:AccelerationNext:Newton's Third Law

Velocity-Time Graphs (Oxford AQA IGCSE Physics)

Revision Note

Calculating Acceleration from a Velocity-Time Graph

Interpreting gradients on a Velocity-Time graphs

Calculating the gradient of a Velocity-Time graph

Worked Example

Examiner Tips and Tricks

Calculating Distance from a Velocity-Time Graph

Calculating the area under a Velocity-Time graph

Worked Example

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Leander Oates

Author: Caroline Carroll