Area under a Velocity-Time Graph (Edexcel IGCSE Physics (Modular))

Revision Note

Test yourself

Written by: Ashika

Reviewed by: Caroline Carroll

Area under a velocity-time graph

How to find the area under a velocity-time graph

The area under a velocity-time graph represents the displacement (or distance travelled) by an object

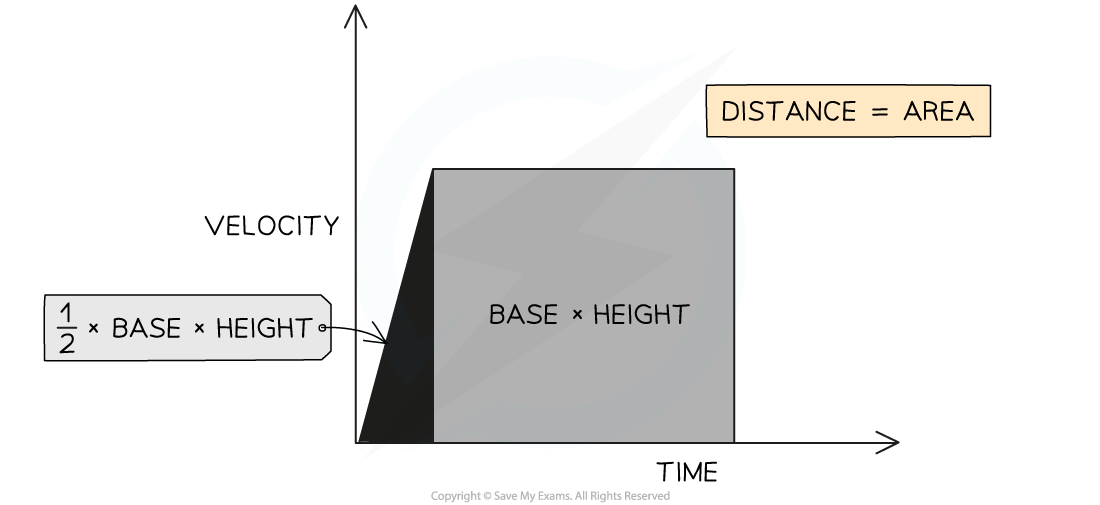
Velocity-Time Area graph, downloadable IGCSE & GCSE Physics revision notes

The displacement, or distance travelled, is represented by the area beneath the graph

If the area beneath the velocity-time graph forms a triangle (i.e. the object is accelerating or decelerating), then the area can be determined by using the following formula:

Area = ½ × Base × Height

If the area beneath the velocity-time graph forms a rectangle (i.e. the object is moving at a constant velocity), then the area can be determined by using the following formula:

Area = Base × Height

How to find distance from a velocity-time graph

Enclosed areas under velocity-time graphs represent total displacement (or total distance travelled) in a time interval

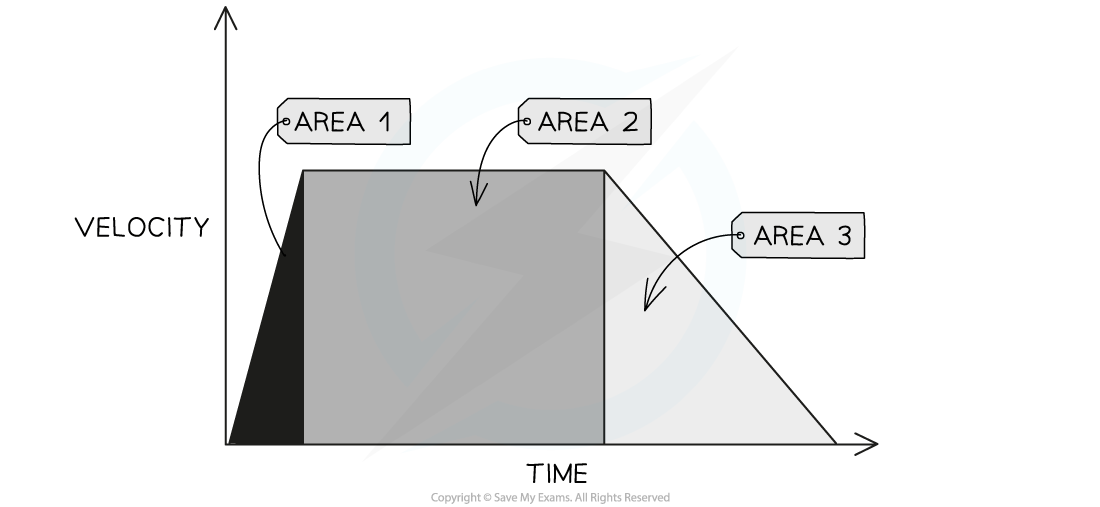
Determining Distance on a V-T graph, downloadable IGCSE & GCSE Physics revision notes

Three enclosed areas (two triangles and one rectangle) under this velocity-time graph represent the total distance travelled in the total time

If an object moves with constant acceleration, its velocity-time graph will consist of straight lines
- In this case, calculate the distance travelled by working out the area of enclosed rectangles and triangles
- The area of each enclosed section represents the distance travelled in that particular interval of time
- The total distance travelled is the sum of all the individual enclosed areas

Worked Example

The velocity-time graph below shows a car journey that lasts for 160 seconds.

Area Under a V-T graph question, downloadable IGCSE & GCSE Physics revision notes

Calculate the total distance travelled by the car.

Answer:

Step 1: Recall that the area under a velocity-time graph represents the distance travelled

In order to calculate the total distance travelled, the total area underneath the line must be determined

Step 2: Identify each enclosed area

In this example, there are five enclosed areas under the line
These can be labelled as areas 1, 2, 3, 4 and 5, as shown in the image below:

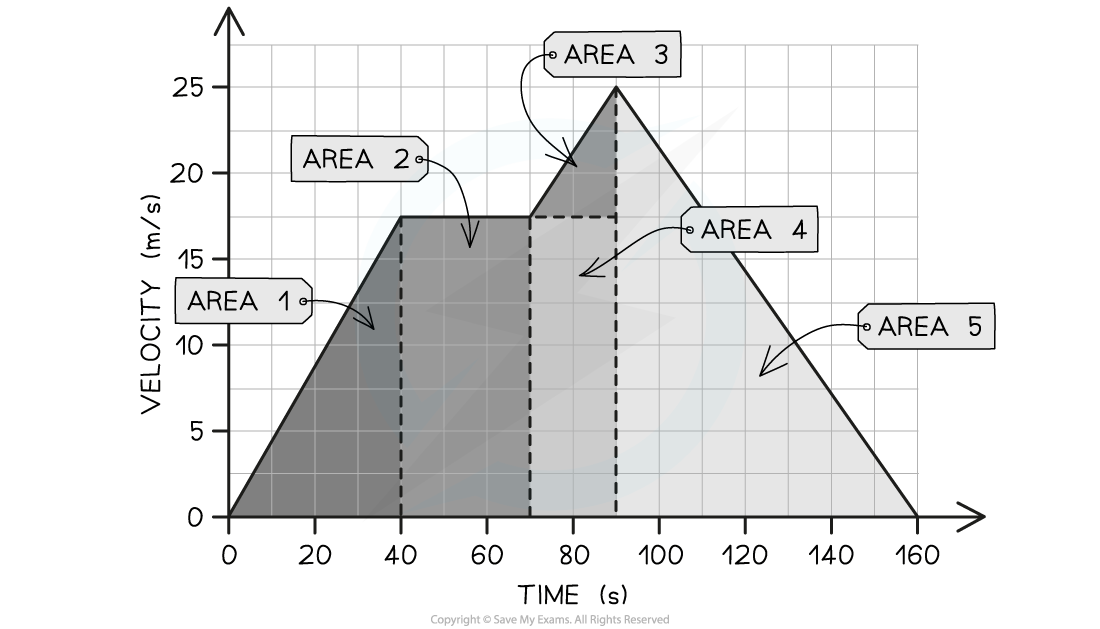
Area Under a V-T graph solution, downloadable IGCSE & GCSE Physics revision notes

Step 3: Calculate the area of each enclosed shape under the line

Area 1 = area of a triangle

$A_{1} = \frac{1}{2} \times base \times height$

$A_{1} = \frac{1}{2} \times 40 \times 17.5$

$A_{1} = 350 m$

Area 2 = area of a rectangle

$A_{2} = base \times height$

$A_{2} = 30 \times 17.5$

$A_{2} = 525 m$

Area 3 = area of a triangle

$A_{3} = \frac{1}{2} \times base \times height$

$A_{3} = \frac{1}{2} \times 20 \times 7.5$

$A_{3} = 75 m$

Area 4 = area of a rectangle

$A_{4} = base \times height$

$A_{4} = 20 \times 17.5$

$A_{4} = 350 m$

Area 5 = area of a triangle

$A_{5} = \frac{1}{2} \times base \times height$

$A_{5} = \frac{1}{2} \times 70 \times 25$

$A_{5} = 875 m$

Step 4: Calculate the total distance travelled by finding the total area under the line

Add up each of the five areas enclosed:

$total distance = A_{1} + A_{2} + A_{3} + A_{4} + A_{5}$

$total distance = 350 + 525 + 75 + 350 + 875$

$total distance = 2175 m$

Examiner Tips and Tricks

Some areas will need to be split into a triangle and a rectangle to determine the area for a specific time interval, like areas 3 & 4 in the worked example above.

If you are asked to find the distance travelled for a specific time interval, then you just need to find the area of the section above that time interval.

For example, the distance travelled between 70 s and 90 s is the sum of Area 3 + Area 4

Last updated: 26 August 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves: