Scalar & Vectors (Edexcel IGCSE Physics (Modular)): Revision Note
Exam code: 4XPH1
Scalar & vector quantities
All quantities can be one of two types:
a scalar
a vector
Scalars
Scalars are quantities that have magnitude but not direction
For example, mass is a scalar quantity because it has magnitude but no direction
Vectors
Vectors are quantities that have both magnitude and direction
For example, weight is a vector quantity because it is a force and has both magnitude and direction
Distance and displacement
Distance is a measure of how far an object has travelled, regardless of direction
Distance is the total length of the path taken
Distance, therefore, has a magnitude but no direction
So, distance is a scalar quantity
Displacement is a measure of how far it is between two points in space, including the direction
Displacement is the length and direction of a straight line drawn from the starting point to the finishing point
Displacement, therefore, has a magnitude and a direction
So, displacement is a vector quantity
What is the difference between distance and displacement?
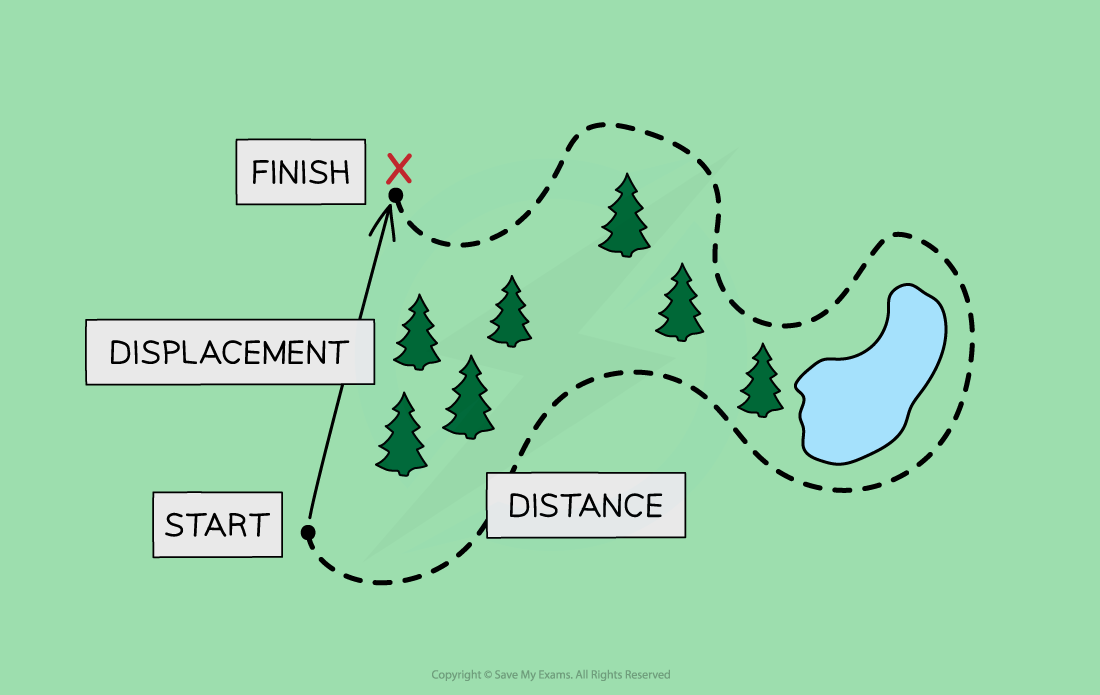
Displacement is a vector quantity while distance is a scalar quantity
When a student travels to school, there will probably be a difference in the distance they travel and their displacement
The overall distance they travel includes the total lengths of all the roads, including any twists and turns
The overall displacement of the student would be a straight line between their home and school, regardless of any obstacles, such as buildings, lakes or motorways, along the way
Speed and velocity
Speed is a measure of the distance travelled by an object per unit time, regardless of the direction
The speed of an object describes how fast it is moving, but not the direction it is travelling in
Speed, therefore, has magnitude but no direction
So, speed is a scalar quantity
Velocity is a measure of the displacement of an object per unit time, including the direction
The velocity of an object describes how fast it is moving and which direction it is travelling in
An object can have a constant speed but a changing velocity if the object is changing direction
Velocity, therefore, has magnitude and direction
So, velocity is a vector quantity
Examples of scalars & vectors
The table below lists some common examples of scalar and vector quantities
Corresponding vectors and their scalar counterparts are aligned in the table where applicable
Table of scalars and vectors
Scalar | Vector |
distance | displacement |
speed | velocity |
mass | weight |
| force |
| acceleration |
| momentum |
energy |
|
volume |
|
density |
|
temperature |
|
power |
|
Worked Example
Astronaut A is in charge of training junior astronauts. For one of their sessions, they would like to explain the difference between mass and weight.
Suggest how Astronaut A should explain the difference between mass and weight, using definitions of scalars and vectors in your answer.
Answer:
Step 1: Recall the definitions of a scalar and vector quantity
Scalar quantities have only a magnitude
Vector quantities have both magnitude and direction
Step 2: Identify which quantity has magnitude only
Mass is a quantity with magnitude only
So mass is a scalar quantity
Astronaut A might explain to the junior astronauts that their mass will not change if they travel to outer space
Step 3: Identify which quantity has magnitude and direction
Weight is a quantity with magnitude and direction (it is a force)
So weight is a vector quantity
Astronaut A might explain to the junior astronauts that their weight will vary depending on their location in space
Forces as vectors
Vector quantities can be represented by arrows
The length of the arrow represents the magnitude
The direction of the arrow indicates the direction
Force is a vector quantity because force has magnitude and direction
When using arrows to represent forces:
the length of the arrow represents the magnitude of the force
the direction of the arrow indicates the direction of the force
the scale of the arrows should be proportional to the relative magnitudes of the forces
an arrow for a 4 N force should be twice as long as an arrow for a 2 N force
the arrows should be labelled with the names of the forces, or a description of the forces
for example, weight, W, or the gravitational pull of the Earth on the object
Two forces acting on an object
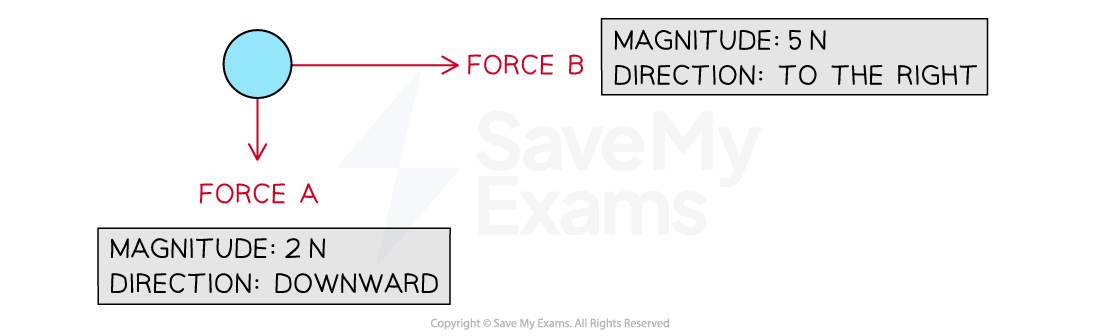
The length of the arrows are proportional to the magnitude of the forces, and show the direction that forces act in
Not all forces are directed perfectly horizontally or vertically and so need to have an angle described for the direction
It is useful to describe an angle with respect to the vertical or the horizontal
A force acting at an angle
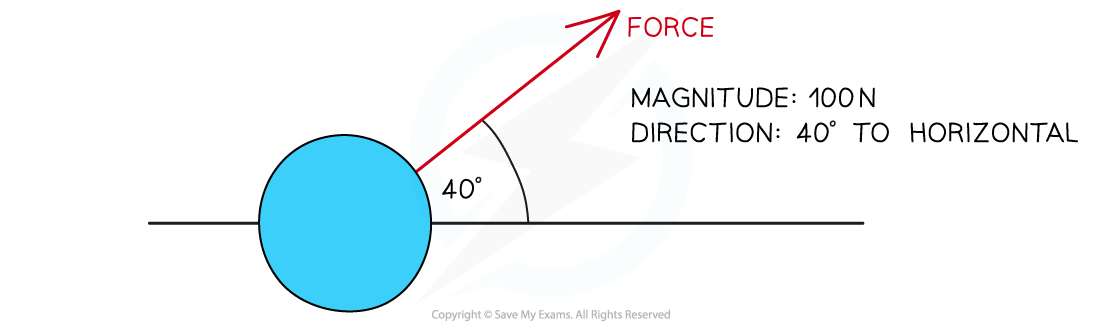
A force of magnitude 100 N directed 40° from the horizontal

Unlock more, it's free!
Did this page help you?