Doppler Shift (Edexcel IGCSE Physics)

Doppler shift

• Usually, when an object emits waves, the wavefronts spread out symmetrically

  • If the wave source moves, the waves can become squashed together or stretched out

• Therefore, when a wave source moves relative to an observer there will be a change in the observed frequency and wavelength

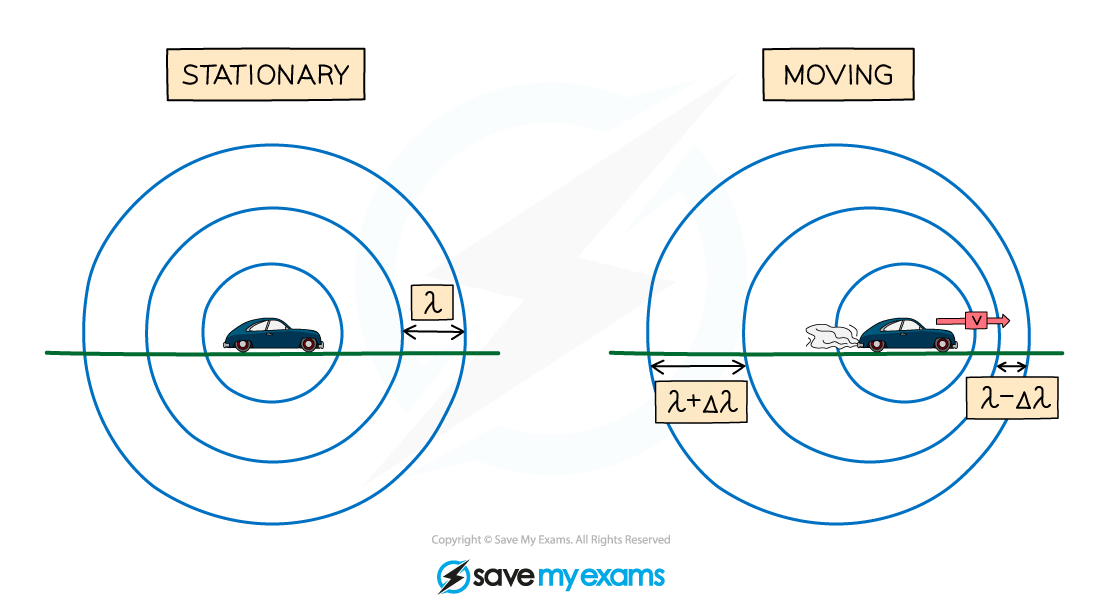
Wavefronts are even in a stationary object but are closer together in the direction of the moving wave source

• A moving object will cause the wavelength, λ, (and frequency) of the waves to change:

  • The wavelength of the waves in front of the source decreases (λ – Δλ) and the frequency increases

  • The wavelength behind the source increases (λ + Δλ) and the frequency decreases

  • This effect is known as the Doppler effect or Doppler shift

• Note: Δλ means 'change in wavelength'

Calculating Doppler shift of light

• Doppler shift can be calculated using the Doppler effect equation:

• Where:

  • λ = observed wavelength of the source in metres (m)

  • λ₀ = reference wavelength in metres (m)

  • Δλ = change in wavelength in metres (m)

  • v = velocity of a galaxy in metres per seconds (m/s)

  • c = the speed of light in metres per second (m/s)

• This means that the change in wavelength, Δλ:

Δλ = λ – λ₀

• The doppler shift equation can be used to calculate the velocity of a galaxy if its wavelength can be measured and compared to a reference wavelength

• Since the fractions have the same units on the numerator (top number) and denominator (bottom number), the Doppler shift has no units