Pressure in Liquids (Edexcel IGCSE Physics): Revision Note

Pressure in liquids

• A fluid is either a liquid or a gas

• When an object is immersed and stationary in a fluid, the fluid will exert pressure, squeezing the object

  • This pressure is exerted evenly across the whole surface of the fluid and in all directions

  • The pressure exerted on objects in fluids creates forces against surfaces

  • These forces act at 90 degrees (at right angles) to the surface

Pressure in a liquid

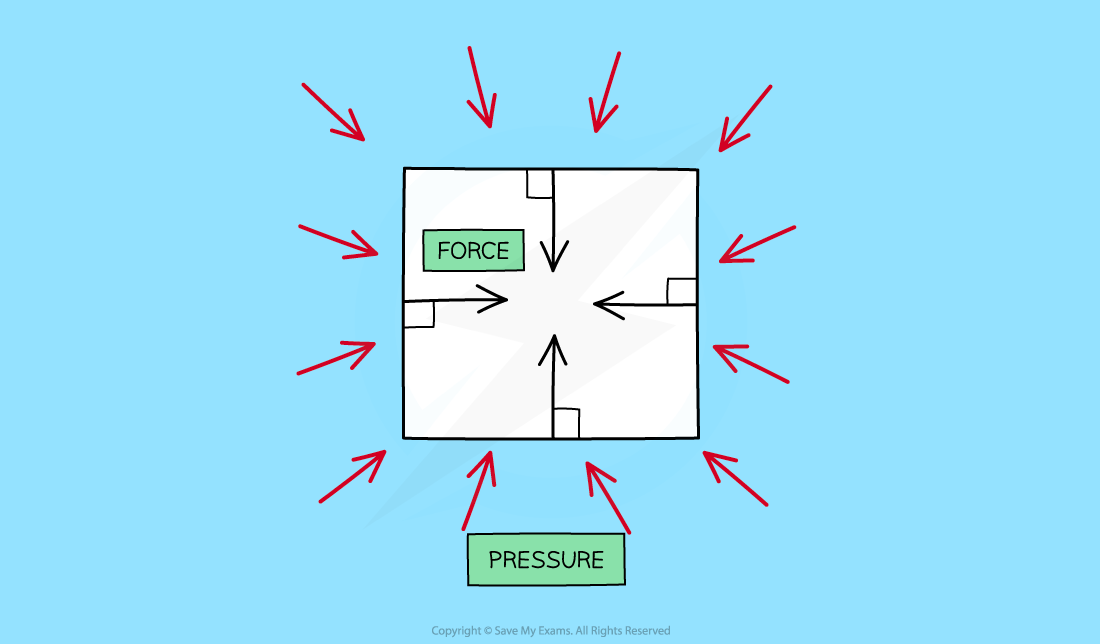
The pressure of a fluid on an object creates a force normal (at right angles) to the surface

Calculating pressure in a liquid

• The pressure acting on an object in a fluid changes with depth

  • The deeper the object then the higher the pressure exerted upon it and vice versa

• The equation for the pressure difference, at different depths, in a fluid is given by the equation:

$P=h\times \rho \times g$

• Where:

  • p = pressure in pascals (Pa)

  • h = height or depth of the fluid column above the object in metres (m)

  • ρ = density of the fluid in kilograms per metre cubed (kg/m³)

  • g = gravitational field strength on Earth in newtons per kilogram (N/kg)

Pressure in a liquid with a density is applied at a depth 

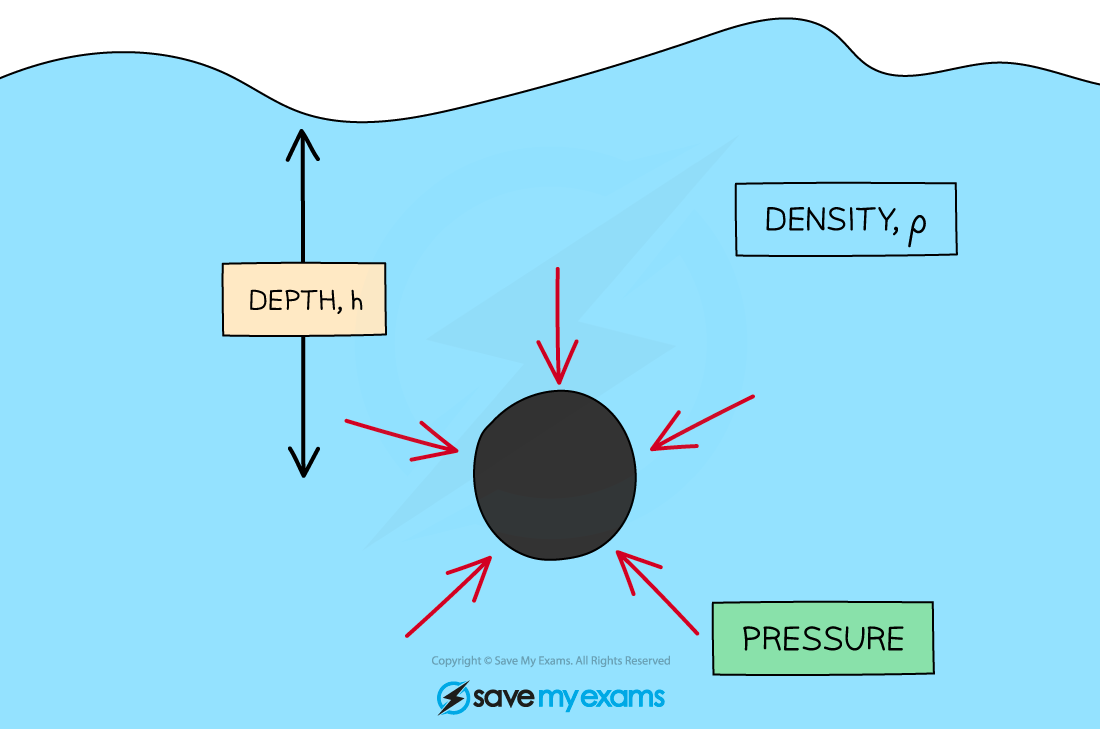
The force from the pressure of objects in a liquid is exerted evenly across its whole surface