Scalar & Vectors (Edexcel IGCSE Physics)

• All quantities can be one of two types:
  • a scalar
  • a vector

Scalars

• Scalars are quantities that have magnitude but not direction
  • For example, mass is a scalar quantity because it has magnitude but no direction 

Vectors

• Vectors are quantities that have both magnitude and direction
  • For example, weight is a vector quantity because it is a force and has both magnitude and direction

Distance and displacement

• Distance is a measure of how far an object has travelled, regardless of direction
  
  • Distance is the total length of the path taken
  • Distance, therefore, has a magnitude but no direction
  • So, distance is a scalar quantity

• Displacement is a measure of how far it is between two points in space, including the direction
  
  • Displacement is the length and direction of a straight line drawn from the starting point to the finishing point
  • Displacement, therefore, has a magnitude and a direction
  • So, displacement is a vector quantity

What is the difference between distance and displacement?

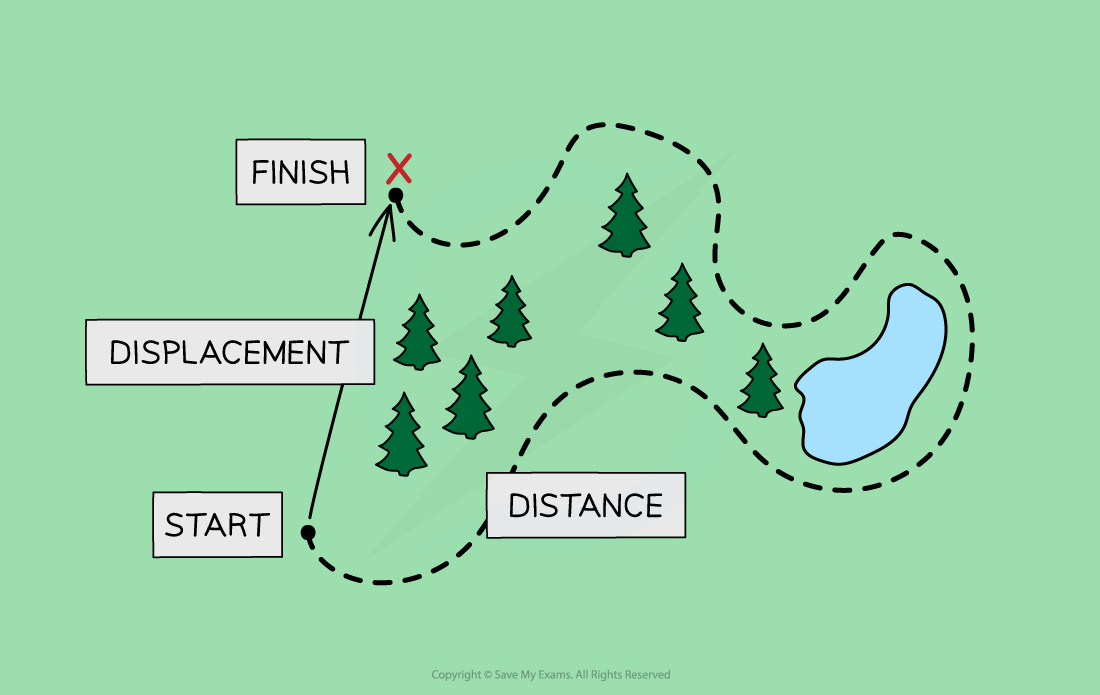
Displacement is a vector quantity while distance is a scalar quantity

• When a student travels to school, there will probably be a difference in the distance they travel and their displacement
  • The overall distance they travel includes the total lengths of all the roads, including any twists and turns
  • The overall displacement of the student would be a straight line between their home and school, regardless of any obstacles, such as buildings, lakes or motorways, along the way

Speed and velocity

• Speed is a measure of the distance travelled by an object per unit time, regardless of the direction
  • The speed of an object describes how fast it is moving, but not the direction it is travelling in
  • Speed, therefore, has magnitude but no direction
  • So, speed is a scalar quantity

• Velocity is a measure of the displacement of an object per unit time, including the direction
  • The velocity of an object describes how fast it is moving and which direction it is travelling in
  • An object can have a constant speed but a changing velocity if the object is changing direction
  • Velocity, therefore, has magnitude and direction
  • So, velocity is a vector quantity

Examples of scalars & vectors

• The table below lists some common examples of scalar and vector quantities
• Corresponding vectors and their scalar counterparts are aligned in the table where applicable

Table of scalars and vectors

Scalar	Vector
distance	displacement
speed	velocity
mass	weight
	force
	acceleration
	momentum
energy
volume
density
temperature
power

• Vector quantities can be represented by arrows
  
  • The length of the arrow represents the magnitude 
  • The direction of the arrow indicates the direction 

• Force is a vector quantity because force has magnitude and direction
• When using arrows to represent forces:
  • the length of the arrow represents the magnitude of the force
  • the direction of the arrow indicates the direction of the force
  • the scale of the arrows should be proportional to the relative magnitudes of the forces
    • an arrow for a 4 N force should be twice as long as an arrow for a 2 N force
  • the arrows should be labelled with the names of the forces, or a description of the forces
    • for example, weight, W, or the gravitational pull of the Earth on the object

Two forces acting on an object

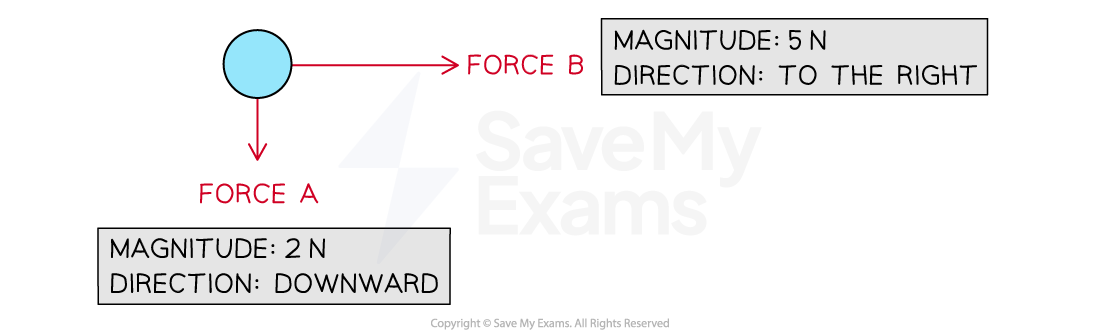
The length of the arrows are proportional to the magnitude of the forces, and show the direction that forces act in

• Not all forces are directed perfectly horizontally or vertically and so need to have an angle described for the direction
  • It is useful to describe an angle with respect to the vertical or the horizontal

A force acting at an angle

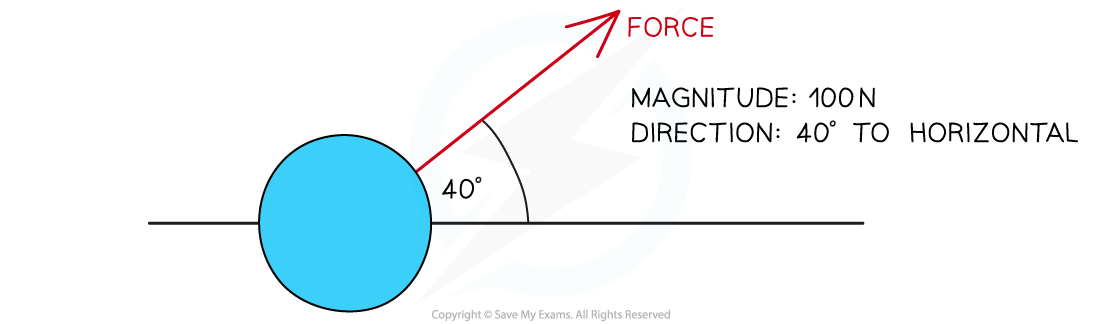
A force of magnitude 100 N directed 40° from the horizontal