Half-Life (Cambridge (CIE) IGCSE Physics): Revision Note

Half-life basics

• The half-life of a particular isotope is defined as:

The time taken for half the nuclei of that isotope in any sample to decay

• The rate at which the activity of a sample decreases is measured in terms of half-life

  • This is the time it takes for the activity of a sample to fall to half its original level

• This is the time it takes for the activity of the sample to decrease from 100 % to 50 %

  • It is the same length of time as it would take to decrease from 50 % activity to 25 % activity

• Different isotopes have different half-lives and half-lives can vary from a fraction of a second to billions of years in length

  • The half-life is constant for a particular isotope

Representing half life

• Half-life can be determined from an activity–time graph

A half-life graph

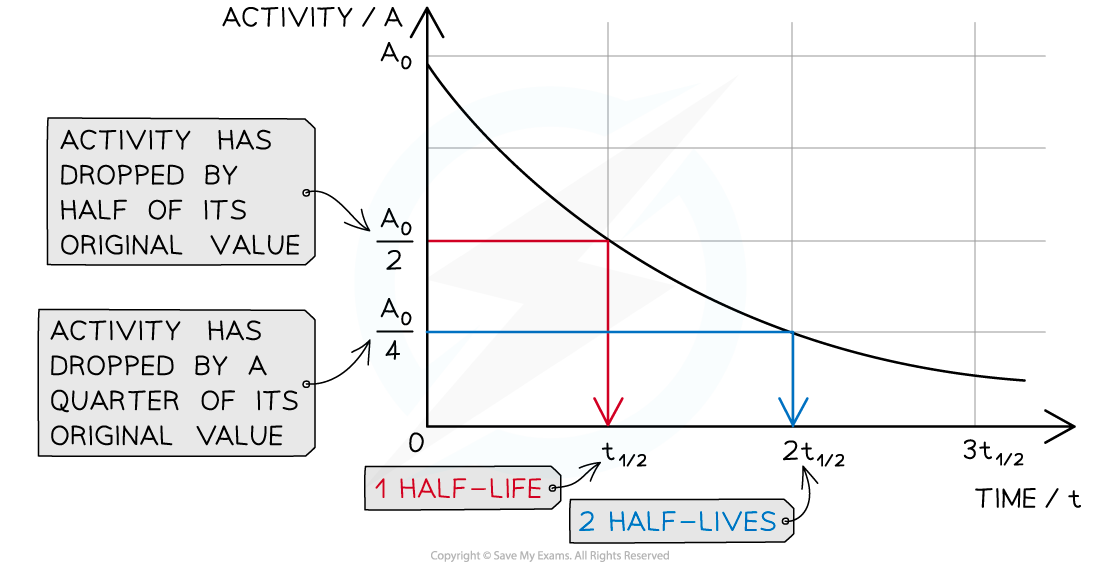
The graph shows how the activity of a radioactive sample changes over time. Each time the original activity halves, another half-life has passed

• Half-life can also be represented on a table

  • As the number of the half-life increases, the proportion of the isotope remaining halves

Table showing the number of half-lives to the proportion of isotope remaining

Half-life graphs

Extended tier only

• The half-life of an isotope should be calculated by removing the background radiation from data or decay curves 

• To calculate the half-life of a sample from a graph:

  • Check the original activity or count rate (where the line crosses the y-axis),C₀

  • Halve this value and look for this activity

  • Go across from the halved value (on the y-axis) to the best-fit curve, and then straight down to the x-axis 

  • The point where you reach the x-axis should be the half-life

Obtaining half-life from a half-life graph

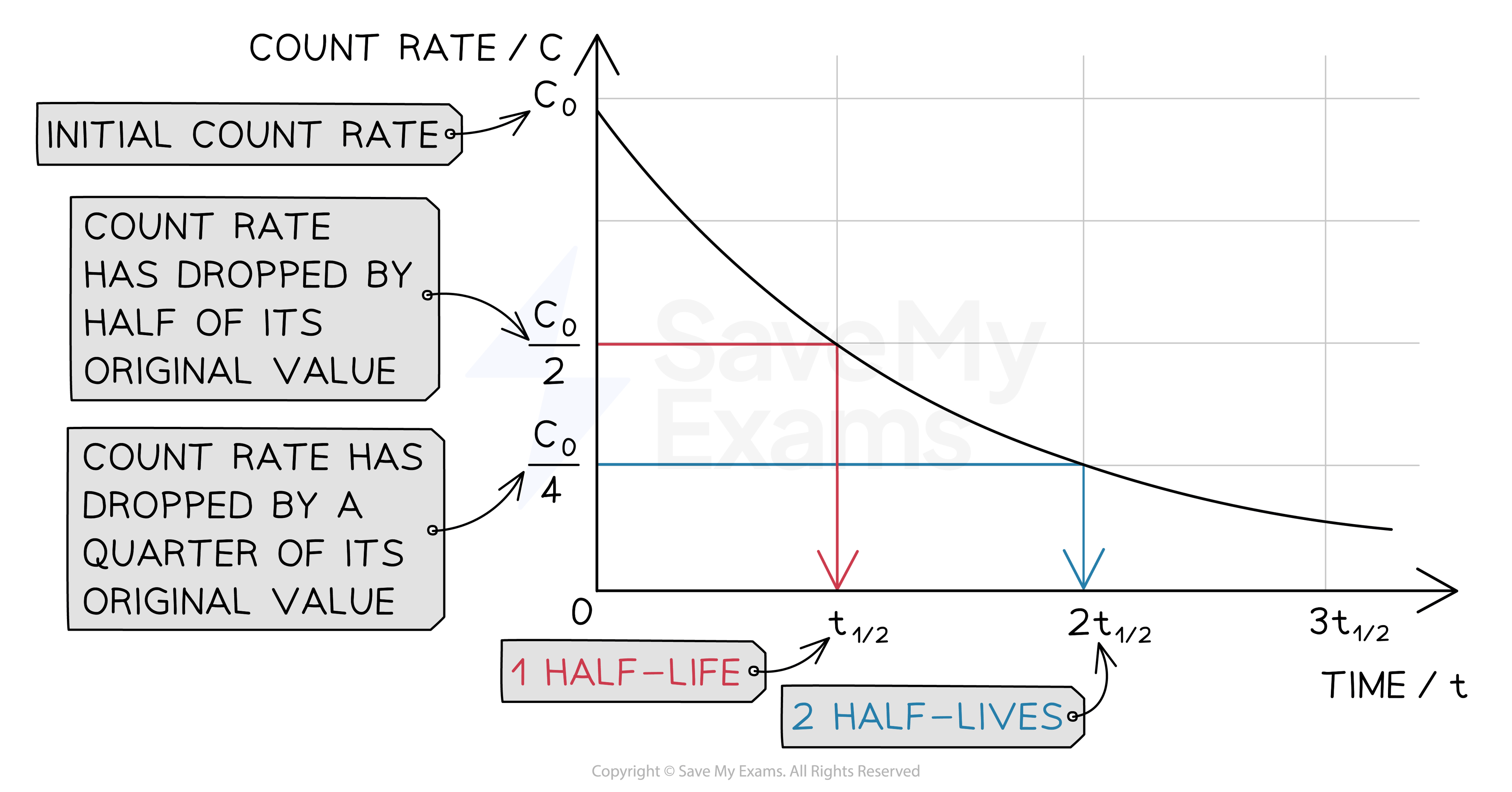
To find the time for the half-life find half of the activity first

• To remove background radiation from the decay curve:

  • Start by measuring the background radiation (with no sources present) – this is called the background count

  • Then carry out the experiment

  • Subtract the background count from each reading, to provide a corrected count

  • The corrected count is your best estimate of the radiation emitted from the source and should be used to measure its half-life

A half-life graph that removes background radiation

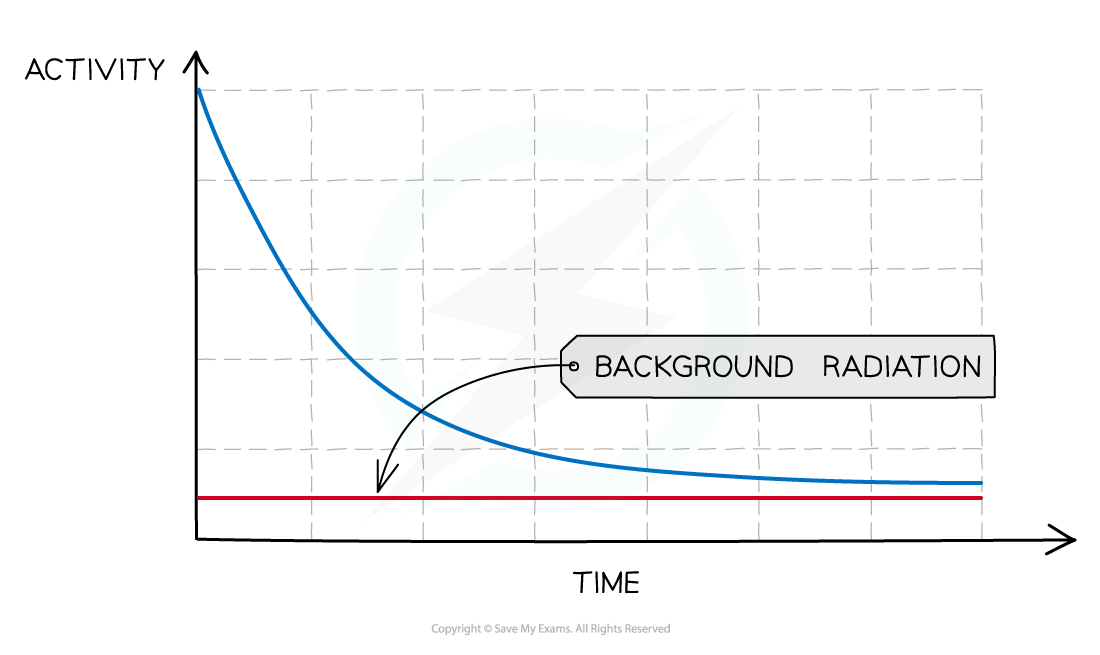
When measuring radioactive emissions, some of the detected radiation will be background