Total Internal Reflection (Cambridge (CIE) IGCSE Physics) : Revision Note
Learn about total internal reflection for your IGCSE Physics exam. This revision note explains the principles of total internal reflection and critical angle.
Did this video help you?
Total internal reflection
Total internal reflection (TIR) occurs at the boundary between two media when:
All the incident ray in medium 1 is reflected back into medium 1
When light passes between the boundary of an optically dense to a less dense medium and the angles of incidence are small
The refracted ray is strong
The reflected ray is weak
The weak ray is reflected back into the denser medium
This means some internal reflection occurs
It is not TIR because not all of the ray is reflected, only some of it
Comparing refraction and total internal reflection

Refraction happens when the angle of incidence is smaller and total internal reflection happens when the angle of incidence equals the angle of reflection
Comparing internal reflection and total internal reflection
Normal reflection produces a less intense light compared to TIR
In TIR the light ray is brighter and more intense
Normal reflection occurs independent of the refractive indices of both media
For TIR to occur, the incident material must be denser than the second material
Conditions for internal reflection

Total internal reflection happens with the angle of incidence is bigger than the critical angle
Internal reflection examples
Thin film interference is an example of internal reflection
An example of this is the shiny side of a CD
Example of internal reflection

The colourful pattern observed on a CD is a result of thin film interference
Other examples of thin film interference include:
Soap bubbles
Thin layers of oil on water
In these examples, internal reflection occurs at the boundaries between:
Air and water
Water and oil
A spectrum of colours will be seen by the observer due to the rays partially reflected at the boundary
A ray diagram of an example of internal reflection

Light is reflected and transmitted at the boundary from a less dense to a more dense material. Light is transmitted only at the boundary from a more dense to a less dense material. Hence, in this diagram P and Q exist but the third unlabelled ray does not.
Total internal reflection examples
Total internal reflection is used to reflect light along optical fibres, meaning they can be used for
communications
endoscopes
decorative lamps
Light travelling down an optical fibre is totally internally reflected each time it hits the edge of the fibre
Total internal reflection example: optical fibre
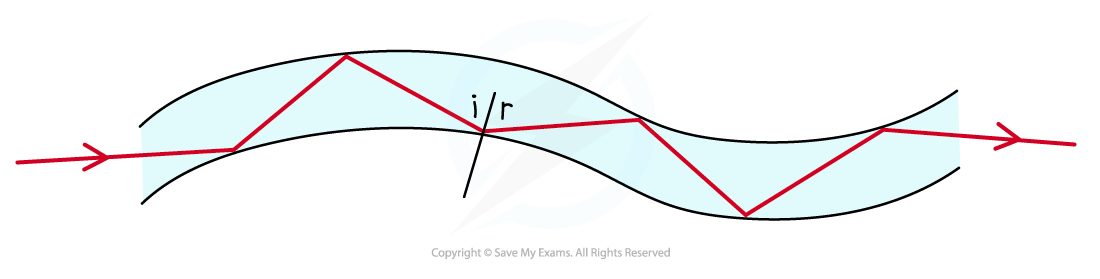
Optical fibres utilise total internal reflection for communications
Prisms are used in a variety of optical instruments, including:
Periscopes
Binoculars
Telescopes
Cameras
Safety reflectors
A periscope is a device that can be used to see over tall objects
It consists of two right-angled prisms
Total internal reflection example: a periscope

Reflection of light through a periscope
The light totally internally reflects in both prisms
Examiner Tips and Tricks
If asked to name the phenomena make sure you give the whole name – total internal reflection
Remember: total internal reflection occurs when light travels from a denser material to less dense material and ALL of the light is reflected.
If asked to give an example of a use of total internal reflection, first state the name of the object that causes the reflection (e.g. a right-angled prism) and then name the device in which it is used (e.g. a periscope)
Critical angle
At the boundary between a more dense and a less dense medium, as the angle of incidence is increased, the angle of refraction also increases until it gets closer to 90°
When the angle of refraction is exactly 90° the light is refracted along the boundary
At this point, the angle of incidence is known as the critical angle c
Obtaining total internal reflection examples

As the angle of incidence increases it will eventually surplus the critical angle and lead to total internal reflection of the light
When the angle of incidence is larger than the critical angle, the refracted ray is now reflected
This is total internal reflection
Worked Example
A glass cube is held in contact with a liquid and a light ray is directed at a vertical face of the cube. The angle of incidence at the vertical face is 39° and the angle of refraction is 25° as shown in the diagram. The light ray is totally internally reflected for the first time at X.
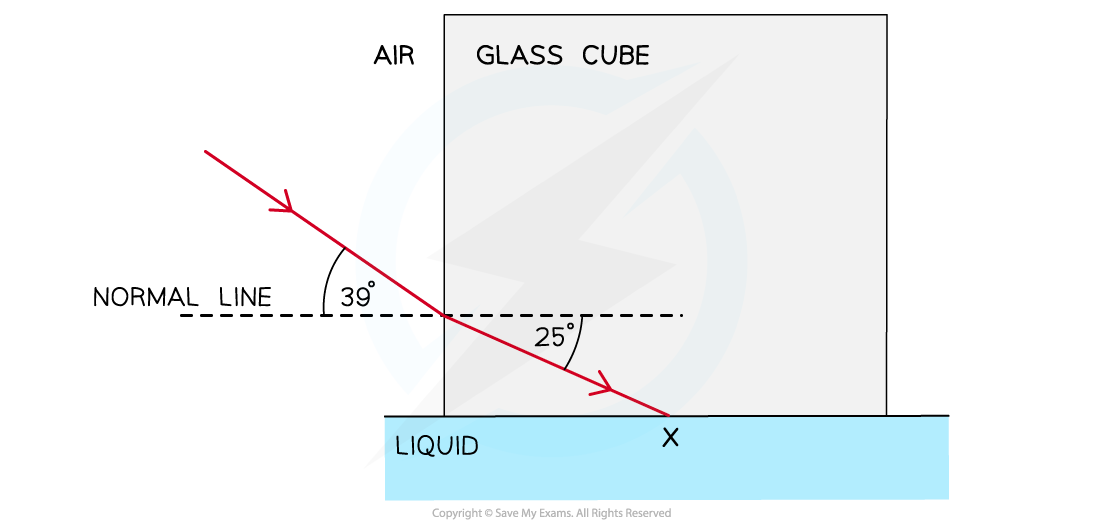
Complete the diagram to show the path of the ray beyond X to the air and calculate the critical angle for the glass-liquid boundary.
Answer:
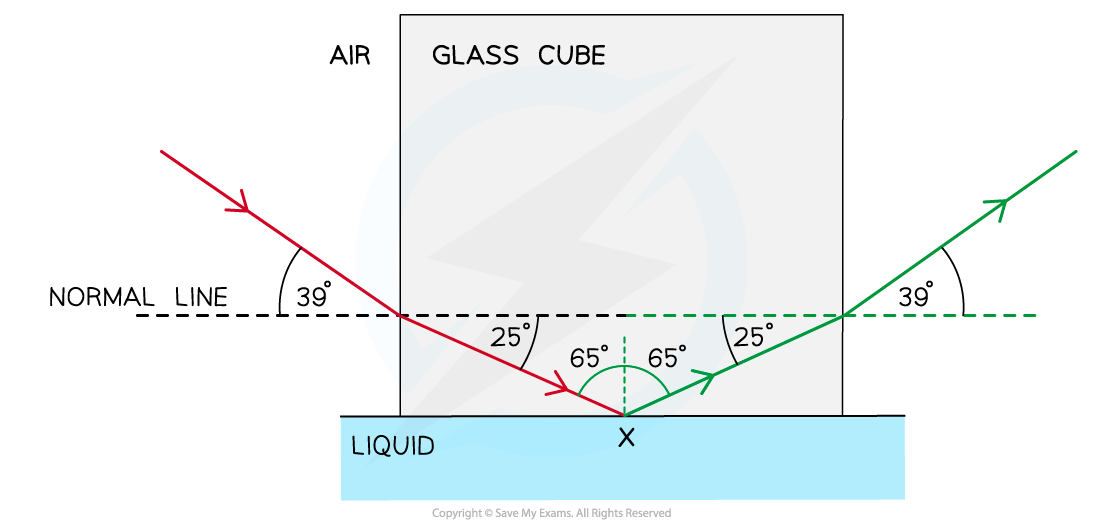
Step 1: Draw the reflected angle at the glass-liquid boundary
When a light ray is reflected, the angle of incidence = angle of reflection
Therefore, the angle of incidence (or reflection) is 90° – 25° = 65°
Step 2: Draw the refracted angle at the glass-air boundary
At the glass-air boundary, the light ray refracts away from the normal
Due to the reflection, the light rays are symmetrical to the other side
Step 3: Calculate the critical angle
The question states the ray is “totally internally reflected for the first time” meaning that this is the lowest angle at which TIR occurs
Therefore, 65° is the critical angle
Examiner Tips and Tricks
If you are asked to explain what is meant by the critical angle in an exam, you can be sure to gain full marks by drawing and labelling the same diagram above (showing the three semi-circular blocks)
Refractive index & critical angle equation
Extended tier only
The critical angle, c, of a material, is related to its refractive index, n
The relationship between the two quantities is given by the equation:
This can also be rearranged to calculate the refractive index, n:
This equation shows that:
The larger the refractive index of a material, the smaller the critical angle
Light rays inside a material with a high refractive index are more likely to be totally internally reflected
Worked Example
Opals and diamonds are transparent stones used in jewellery. Jewellers shape the stones so that light is reflected inside. Compare the critical angles of opal and diamond and explain which stone would appear to sparkle more.
The refractive index of opal is about 1.5
The refractive index of diamond is about 2.4
Answer:
Step 1: List the known quantities
Refractive index of opal, no = 1.5
Refractive index of diamond, nd = 2.4
Step 2: Write out the equation relating critical angle and refractive index
Step 3: Calculate the critical angle of opal (co)
Step 4: Calculate the critical angle of diamond (cd)
Step 5: Compare the two values and write a conclusion
Total internal reflection occurs when the angle of incidence of light is larger than the critical angle (i > c)
In opal, total internal reflection will occur for angles of incidence between 42° and 90°
The critical angle of diamond is lower than the critical angle of opal (co > cd)
This means light rays will be totally internally reflected in diamond over a larger range of angles (25° to 90°)
Therefore, more total internal reflection will occur in diamond hence it will appear to sparkle more than the opal
Examiner Tips and Tricks
When calculating the value of the critical angle using the above equation:
First use the refractive index, n, to find sin(c)
Then use the inverse sin function (sin–1) to find the value of c
Optical fibres
Extended tier only
Optical fibres have many uses, particularly in telecommunications
Endoscopes are used to look within the human body
A camera on the end of an optical fibre is placed down the throat and moved into the stomach
Light from inside the stomach is captured by the camera, is totally internally reflected along the optical fibre and viewed by doctors through the eyepiece
Total internal reflection example: endoscope
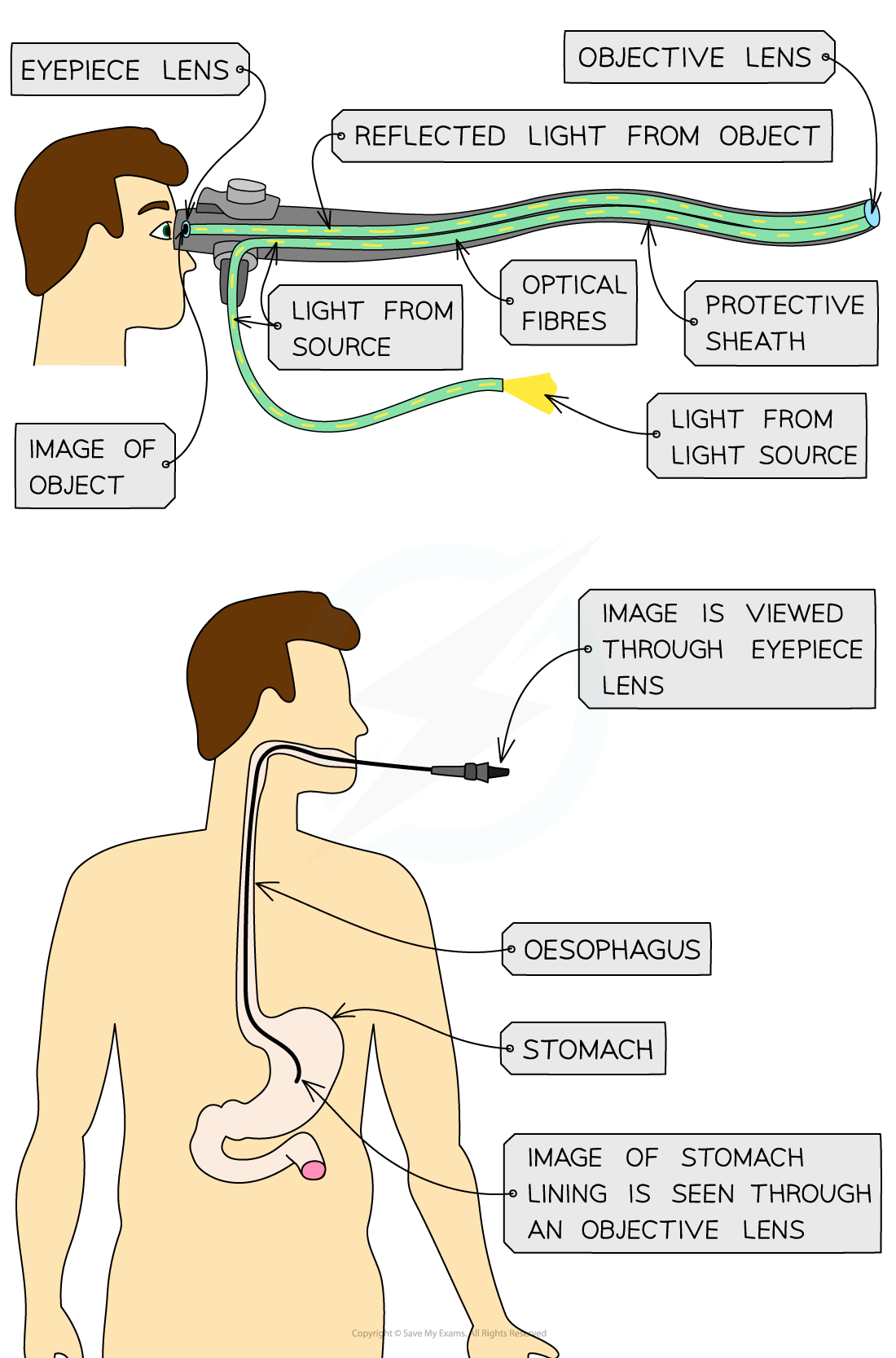
Endoscopes utilise total internal reflection to see inside a patient's body
Total internal reflection using telecommunication
Optical fibres can be used to transmit:
Home (landline) telephone signals
Internet signals
Cable television signals
In phone calls from landline phones:
Electrical signals are converted to light pulses
That travel close to the speed of light along optical fibres
At the receiving end, the digital signal is converted into sound
Total internal reflection example: landline telephone signal path

Sound from a landline telephone travels through optical fibres to the landline of the person listening
Optical fibres are installed:
In cables attached to telephone (or telegraph) poles in the street
Underground from the service box to the telegraph pole or under the sea
Total internal reflection example: telegraph poles

Fibre optic cables can be found in the phone cables attached between the telephone poles and the street

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

