Pressure & Forces (Cambridge (CIE) IGCSE Physics): Revision Note
Exam code: 0625 & 0972
Did this video help you?
Pressure
What is pressure?
Pressure is defined as
The force per unit area
Pressure is measured in pascals (Pa)
1 pascal is equivalent to 1 newton per metre squared
1 Pa = 1 N/m2
It can be calculated using the following pressure equation:
Where:
p = pressure measured in pascals (Pa) or newtons per metre (N/m2)
F = force measured in newtons (N)
A = area measured in metres squared (m2)
This equation can be rearranged with the help of a formula triangle:

A formula triangle can help rearrange the pressure equation
For more information on how to use a formula triangle refer to the revision note on speed & velocity
This equation tells us that:
If a force is spread over a large area it will result in a small pressure
If it is spread over a small area it will result in a large pressure
Examples of applications of pressure
Example 1: Tractors
Tractors have large tyres
This spreads the weight (force) of the tractor over a large area
This reduces the pressure which prevents the heavy tractor from sinking into the mud
Example 2: Drawing pins
Drawing pins have sharp pointed ends with a very small area
This concentrates the force, creating a large pressure over a small area
This allows the drawing pin to be pushed into a wall
Applying a force to a drawing pin
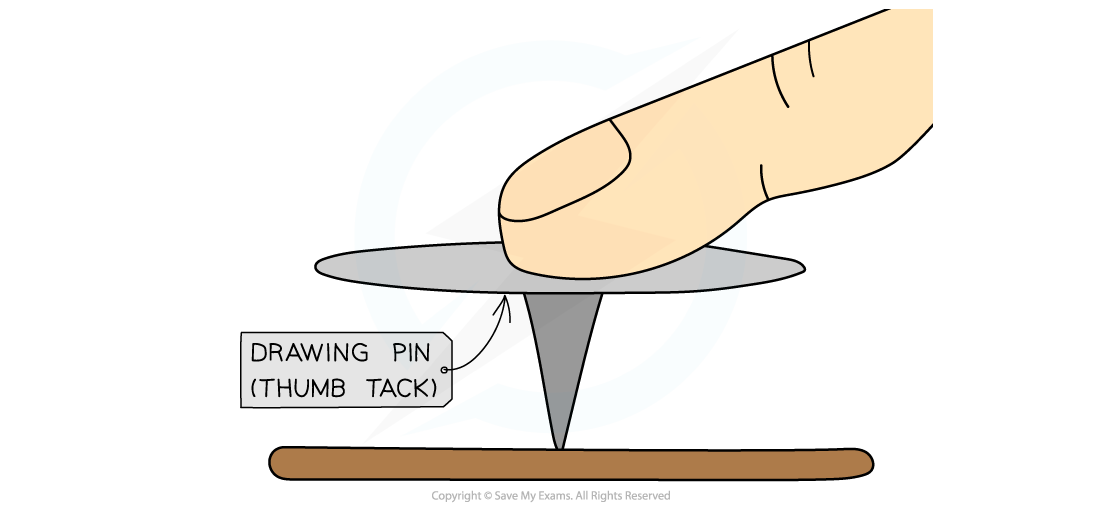
When you push a drawing pin, it goes into the surface (rather than your finger)
Example 3: High heels
High heels have small, sharp points with a small area
This concentrates the weight (force), creating a large pressure over a small area
Flat shoes have a larger area which the weight (force) is spread over resulting in a lower pressure
This explains why high heels sink into soft surfaces more easily than flat shoes
The effect of surface area on pressure
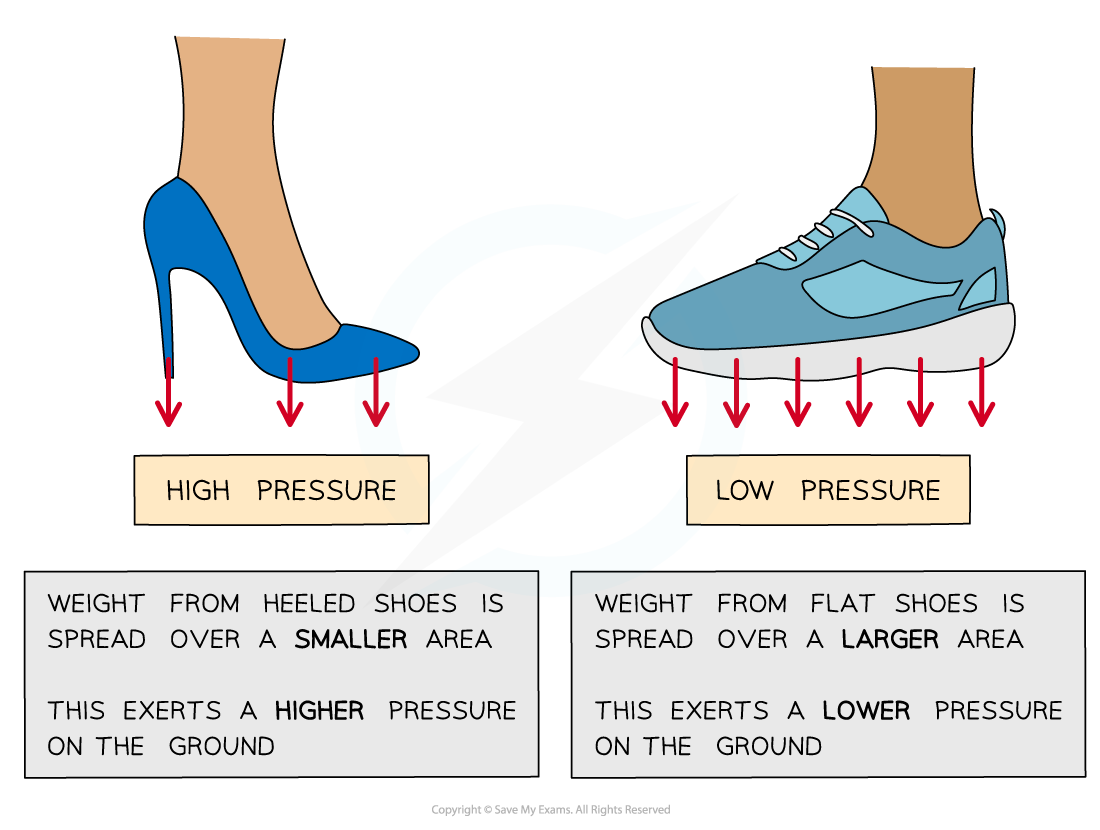
High heels produce a higher pressure on the ground because of their smaller area, compared to flat shoes
Worked Example
The diagram below shows the parts of the lifting machine used to move the platform up and down.
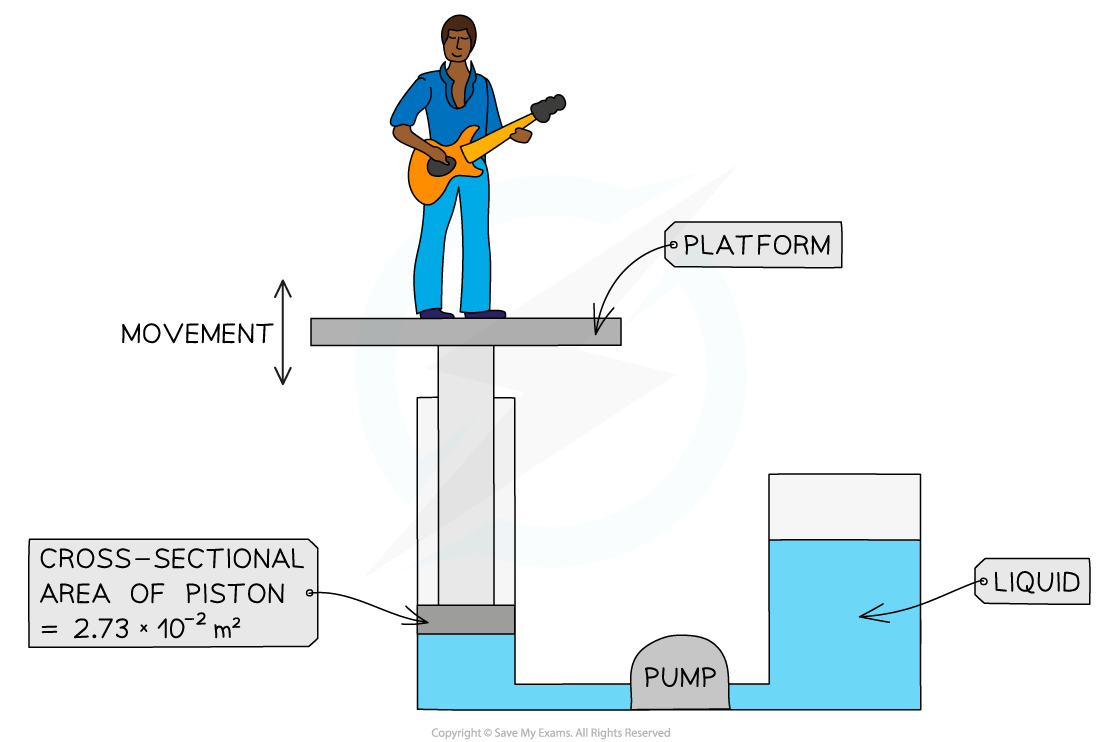
The pump creates pressure in the liquid of 5.28 × 105 Pa to move the platform upwards.
Calculate the force that the liquid applies to the piston.
Answer:
Step 1: List the known quantities
Cross-sectional area = 2.73 × 10-2 m2
Pressure = 5.28 × 105 Pa
Step 2: Write down the relevant equation
Step 3: Rearrange for the force, F
Step 4: Substitute the values into the equation
Step 5: Round to the appropriate number of significant figures and quote the correct unit
Did this video help you?

Unlock more, it's free!
Did this page help you?