Hooke's Law (Cambridge (CIE) IGCSE Physics): Revision Note
Exam code: 0625 & 0972
Hooke's law
Extended tier only
The relationship between the extension of an elastic object and the applied force is defined by Hooke's Law
Hooke's Law states that:
The extension of an elastic object is directly proportional to the force applied, up to the limit of proportionality
Directly proportional means that as the force is increased, the extension increases
If the force is doubled, then the extension will double
If the force is halved, then the extension will also halve
The limit of proportionality is the point beyond which the relationship between force and extension is no longer directly proportional
This limit varies according to the material
The extension of a spring due to an applied load
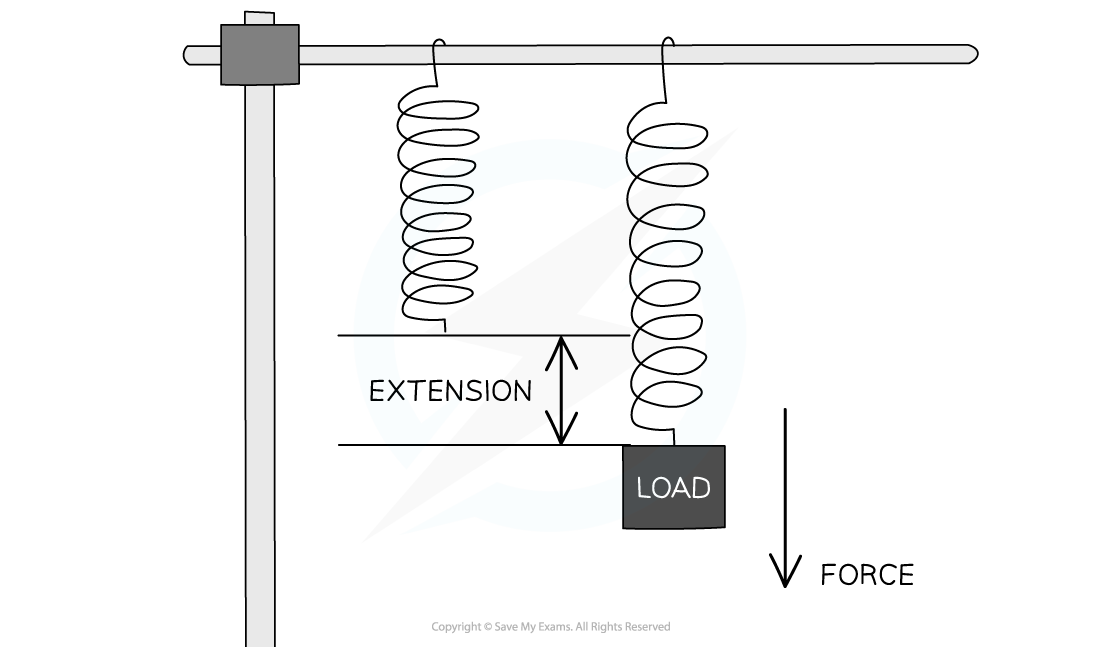
Hooke's Law states that a force applied to a spring will cause it to extend by an amount proportional to the force
Hooke's law can be described by the following equation:
Where:
= force applied, measured in newtons (N)
= the spring constant, measured in newtons per metre (N/m)
= extension of spring, measured in metres (m)
The force applied to the spring is sometimes referred to as the load
Spring constant
The spring constant is defined as:
The force per unit extension
Therefore, the units are newtons per metre (N/m)
The spring constant is a measure of how stiff the spring is
Stiff springs have a high spring constant
Stretchy springs have a low spring constant
The spring constant can be applied to objects other than springs
The Hooke's law equation can be used to calculate the spring constant of a material
The force-extension graph
Hooke’s law is a linear relationship
This is represented by a straight line on a force-extension, or load-extension graph
Any material beyond its limit of proportionality will have a non-linear relationship between force and extension
Force-extension graph for a spring

Hooke's Law is associated with the linear region of a force-extension graph. Beyond the limit of proportionality, Hooke's law no longer applies
Important features of the force-extension graph
The linear portion of the graph
This represents the load or force under which the spring obeys Hooke's law
Force and extension are directly proportional
The gradient of the linear portion is equal to the spring constant for a force-extension graph
The gradient of the linear portion is equal to
for an extension-force graph
The limit of proportionality
This is the point at which the graph begins to curve
Beyond this point, force and extension are no longer proportional
The curved portion of the graph
This is where the material does not obey Hooke's law
Force and extension are not proportional
Worked Example
The figure below shows the forces acting on a child who is balancing on a pogo stick. The child and pogo stick are not moving.
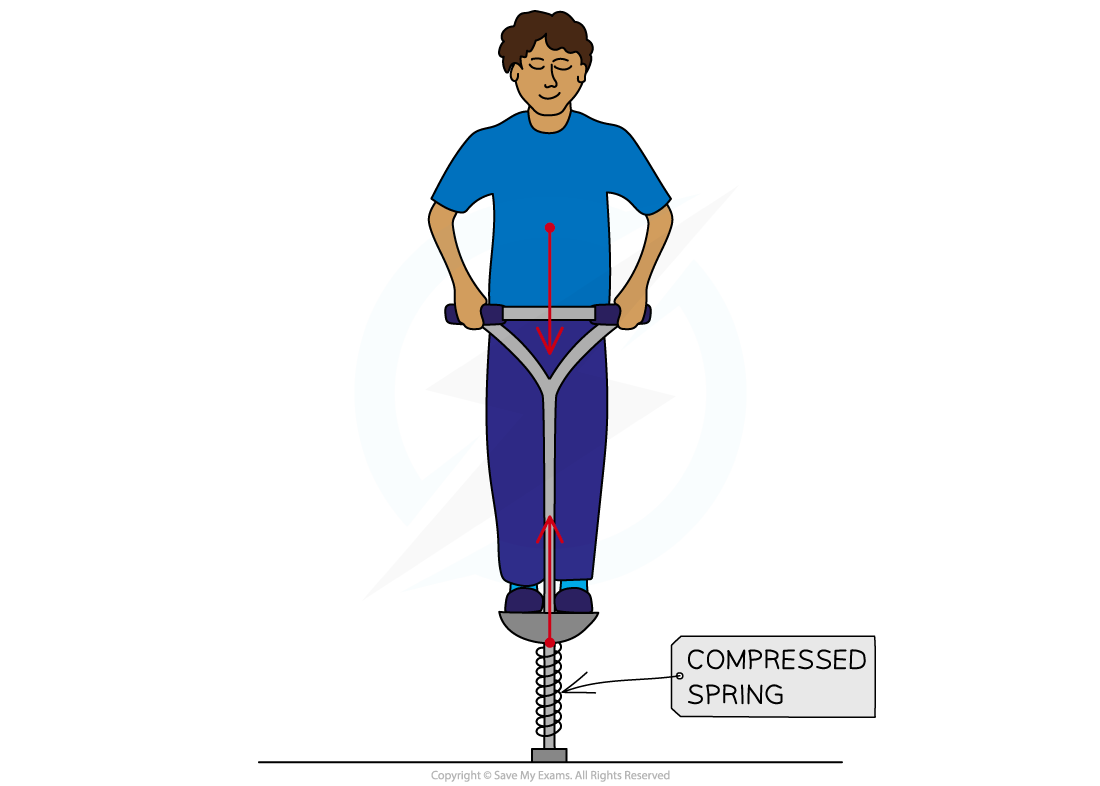
The spring constant of the spring on the pogo stick is 4900 N/m. The weight of the child causes the spring to compress elastically from a length of 40 cm to a new length of 33 cm.
Calculate the weight of the child.
Answer:
Step 1: List the known quantities
Spring constant, k = 4900 N/m
Original length = 40 cm
Final length = 33 cm
Step 2: Write the relevant equation
Step 3: Calculate the compression, x
A negative extension represents a compression of 7 cm
Step 4: Convert any units
Since the spring constant is given in N/m,
must be in metres (m)
Step 5: Substitute the values into the Hooke's Law equation
The minus sign simply indicates the direction of the force, downwards in this case
The child's weight is 343 N

Unlock more, it's free!
Did this page help you?