IGCSEPhysicsCambridge (CIE)Revision Notes1. Motion, Forces & EnergyMotionDistance-Time Graphs

Distance-Time Graphs (Cambridge (CIE) IGCSE Physics)

Revision Note

Test yourselfFlashcards
Leander Oates

Written by: Leander Oates

Reviewed by: Caroline Carroll

Did this video help you?

Distance-time graphs

  • A distance-time graph is used to describe the motion of an object and calculate its speed

Distance-time graph of an object moving at a constant speed

Distance -Time Graph 1, downloadable IGCSE & GCSE Physics revision notes

The graph shows a moving object moving further away from its origin at a constant speed

Constant speed on a distance-time graph

  • If an object is moving at a constant speed, the distance-time graph will be a straight line

    • If the constant speed is zero, the line will be horizontal

    • If the constant speed is non-zero, the line will have a gradient

  • If an object has a speed of zero, the object is stationary

    • The distance moved by the object over time is zero

  • The gradient of a distance-time graph represents the magnitude of the object's velocity, or its speed

    • A steeper slope, or a higher gradient, represents a greater speed

    • A shallower slope, or a lower gradient, represents a slower speed

Different speeds on a distance-time graph

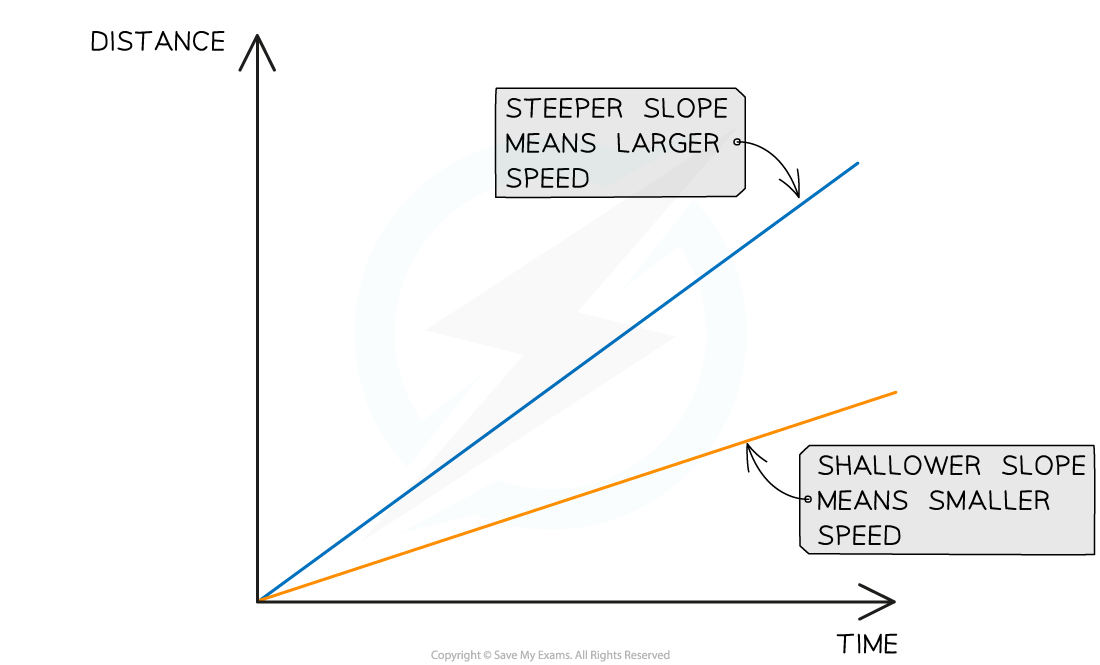
Distance -Time Graph 2, downloadable IGCSE & GCSE Physics revision notes

Both of these objects are moving at a constant speed, because the lines are straight. The steeper slope represents the faster speed and the shallower line represents the slower speed.

Changing speed on a distance-time graph

  • Often, the speed of an object is not constant

  • If the speed of an object is changing, the object is accelerating

  • If an object is accelerating, the distance-time graph will be a curved line

  • A curve on a distance-time graph is a changing gradient

    • If the gradient increases over time, the speed is increasing over time

    • If the gradient decreases over time, the speed is decreasing over time

Speed of an object increasing and decreasing on a distance-time graph

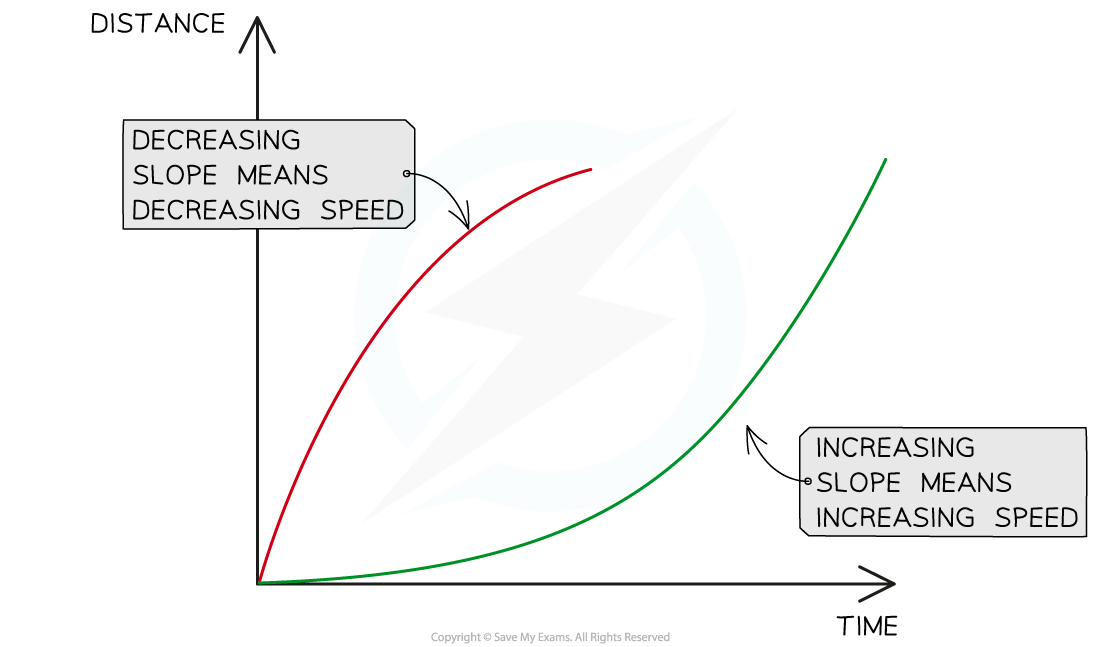
Distance -Time Graph 3, downloadable IGCSE & GCSE Physics revision notes

Changing speeds are represented by changing slopes, or gradients. The red line shows a decreasing gradient and represents an object slowing down, or decelerating. The green line shows an increasing gradient and represents an object speeding up, or accelerating.

Using distance-time graphs

  • The speed of a moving object can be calculated from the gradient of the line on a distance-time graph:

speed space equals space gradient space equals space fraction numerator increment y over denominator increment x end fraction

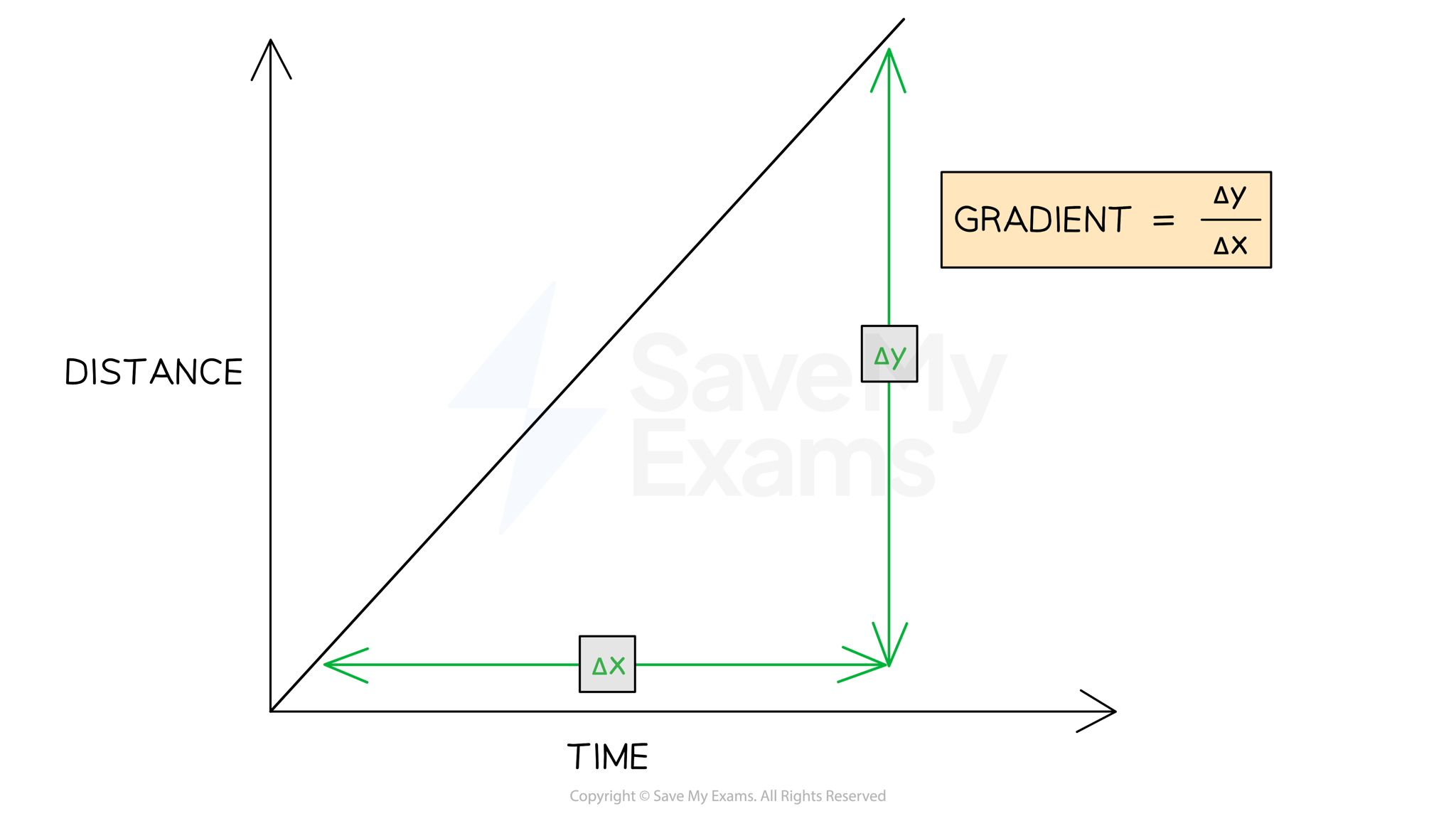
gradient-distance-time-graph-xy

The speed of an object can be found by calculating the gradient of a distance-time graph

  • increment y is the change in y (distance) values

  • increment x is the change in x (time) values

Worked Example

A distance-time graph is drawn below for part of a train journey. The train is travelling at a constant speed.

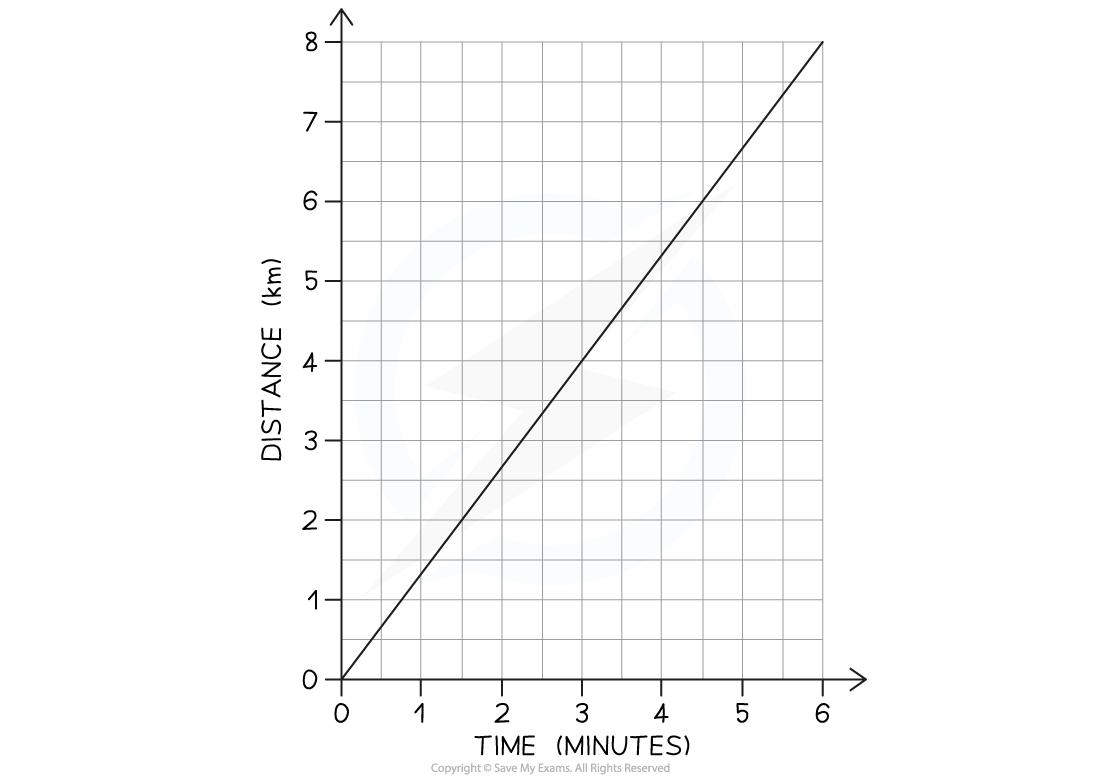
WE Gradient of D-T question graph, downloadable IGCSE & GCSE Physics revision notes

Calculate the speed of the train.

 

Answer:

Step 1: Draw a large gradient triangle on the graph 

  • The image below shows a large gradient triangle drawn with dashed lines

  • increment y and increment x are labelled, using the units as stated on each axes

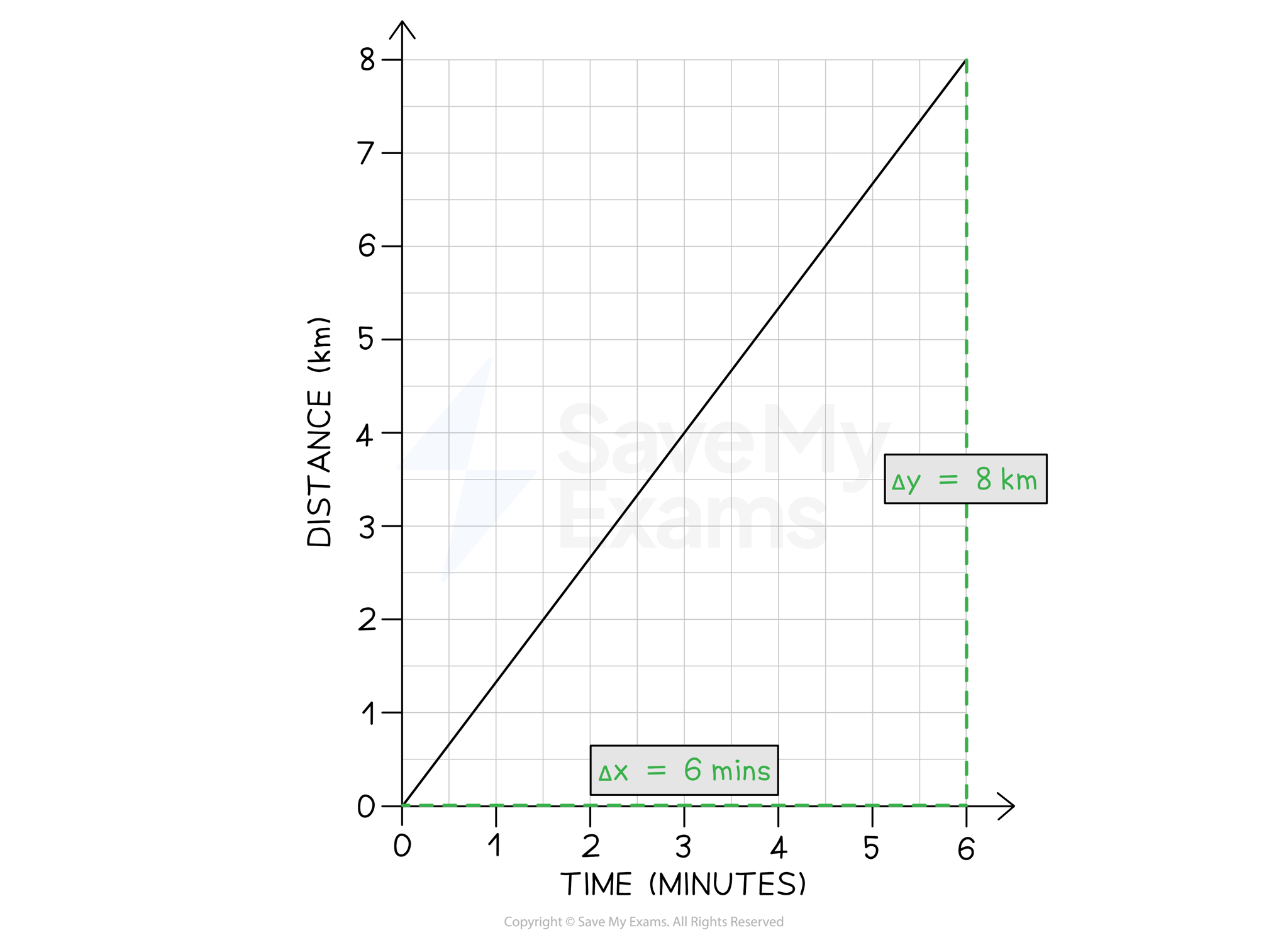
gradient-of-distance-time-graph-we1

Step 2: Convert units for distance and time into standard units

  • The distance travelled, s space equals space 8 space km space cross times space 1000 space straight m space equals space 8000 space straight m 

  • The time taken, t space equals space 6 space min space cross times space 60 space straight s equals space 360 space straight s

Step 3: State that speed is equal to the gradient of a distance-time graph

  • The gradient of a distance-time graph is equal to the speed of a moving object:

gradient space equals space v space equals space fraction numerator increment y over denominator increment x end fraction space equals space s over t

Step 4: Substitute values to calculate the speed

v space equals fraction numerator space 8000 over denominator 360 end fraction

v space equals space 22.2 space straight m divided by straight s

Worked Example

A student decides to take a stroll to the park. They find a bench in a quiet spot, take a seat, and read a book on black holes. After some time reading, the student realises they lost track of time and runs home.

A distance-time graph for the trip is drawn below.

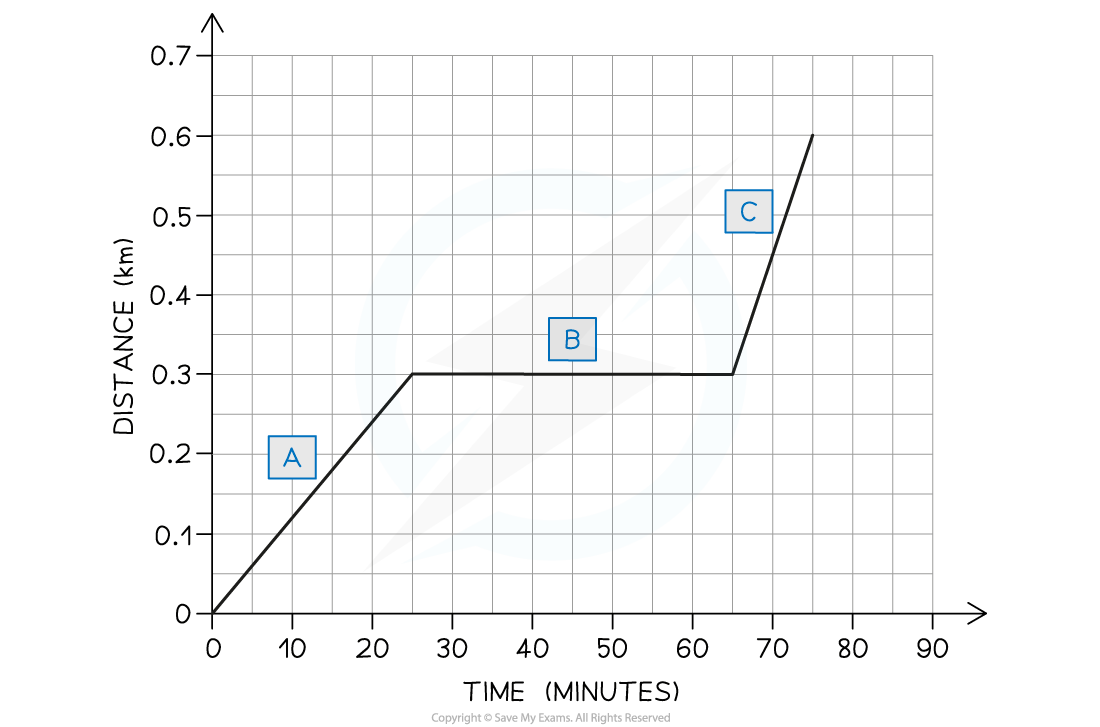
WE Ose gets carried away Question image, downloadable IGCSE & GCSE Physics revision notes

(a) How long does the student spend reading the book?

(b) Which section of the graph represents the student running home?

(c) What is the total distance travelled by the student?

 

Answer:

Part (a)

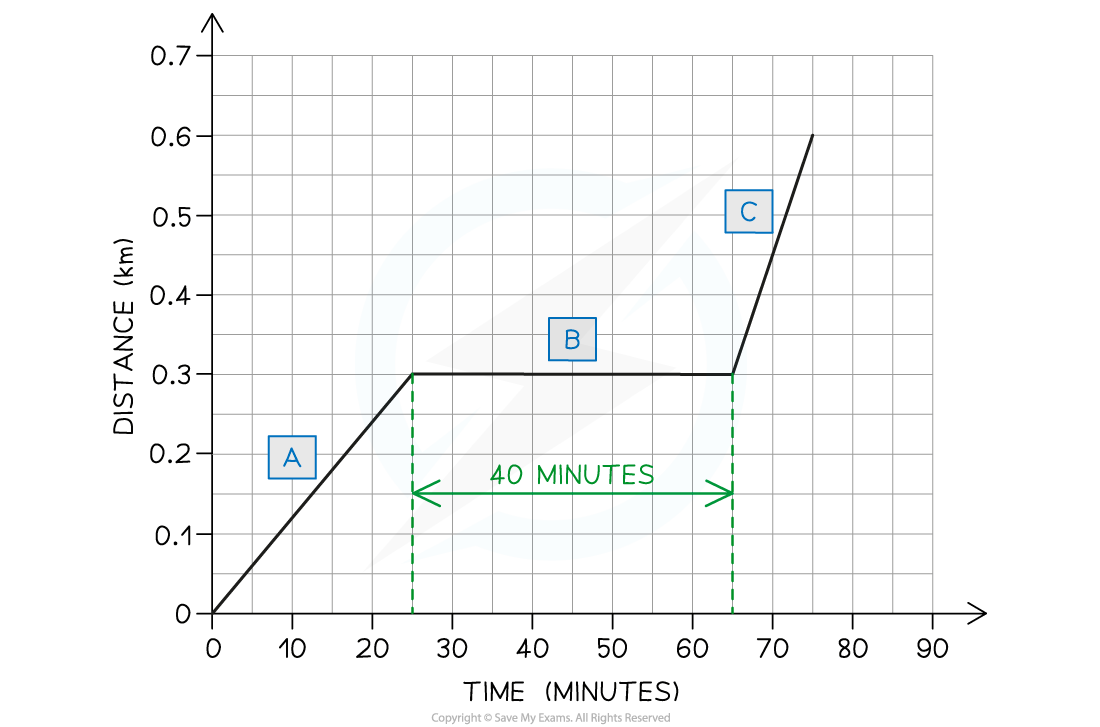
  • The student spends 40 minutes reading his book

  • The flat section of the line (section B) represents an object which is stationary, so section B represents the student sitting on the bench reading

  • This section lasts for 40 minutes 

WE Ose gets carried away Ans a, downloadable IGCSE & GCSE Physics revision notes

Part (b)

  • Section C represents the student running home

  • The slope of the line in section C is steeper than the slope in section A

  • This means the student was moving at a faster speed (running) in section C

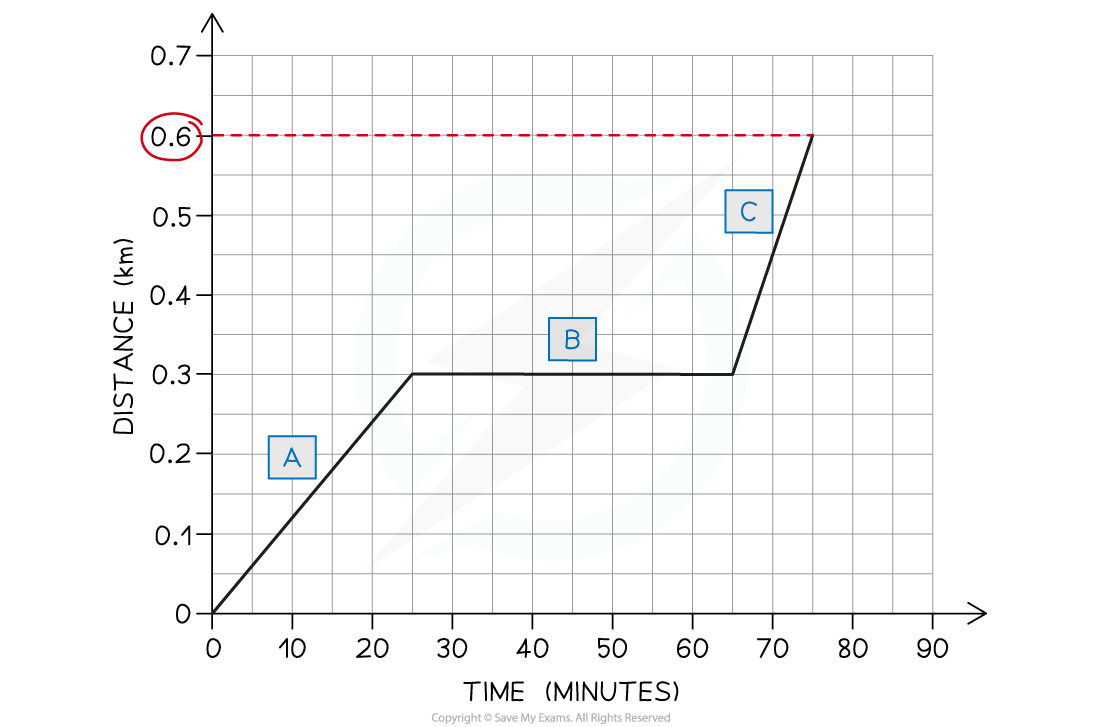
Part (c)

  • The total distance travelled by the student is 0.6 km

  • The total distance travelled by an object is given by the final point on the line; in this case, the line ends at 0.6 km on the distance axis

WE Ose gets carried away Ans c, downloadable IGCSE & GCSE Physics revision notes

Examiner Tips and Tricks

When calculating a gradient, use the entire line where possible. Examiners tend to award credit if they see a large gradient triangle used, so you need to actually draw the lines directly on the graph itself!

Remember to check the units on each axis. These may not always be in standard units; in our example, the unit of distance was km and the unit of time was minutes. Double-check which units to use in your answer.

You could also be asked to plot a distance time graph from data given to you in a question, or be asked to describe the motion of an object from the data given.

You can read more about the use of graphs in exams in the article Graph skills for GCSE Physics

Last updated:

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:AccelerationNext:Speed-Time Graphs
    Author
    Reviewer
    Leander Oates

    Author: Leander Oates

    Expertise: Physics

    Leander graduated with First-class honours in Science and Education from Sheffield Hallam University. She won the prestigious Lord Robert Winston Solomon Lipson Prize in recognition of her dedication to science and teaching excellence. After teaching and tutoring both science and maths students, Leander now brings this passion for helping young people reach their potential to her work at SME.

    Caroline Carroll

    Author: Caroline Carroll

    Expertise: Physics Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.