Moments (Cambridge (CIE) IGCSE Physics): Revision Note
Did this video help you?
Moments
The moment of a force is the turning effect produced when a force is exerted on an object
Examples of the turning effect of a force are:
A child on a see-saw
Turning the handle of a spanner
A door opening and closing
Using a crane to move building supplies
Using a screwdriver to open a tin of paint
Turning a tap on and off
Picking up a wheelbarrow
Using scissors
Forces can cause the rotation of an object about a fixed pivot
This rotation can be clockwise or anticlockwise
Clockwise and anti-clockwise rotation
Consider the hands of a clock when deciding if an object will rotate in a clockwise or anti-clockwise direction
A force applied on one side of the pivot will cause the object to rotate
Turning effect of a force about a pivot
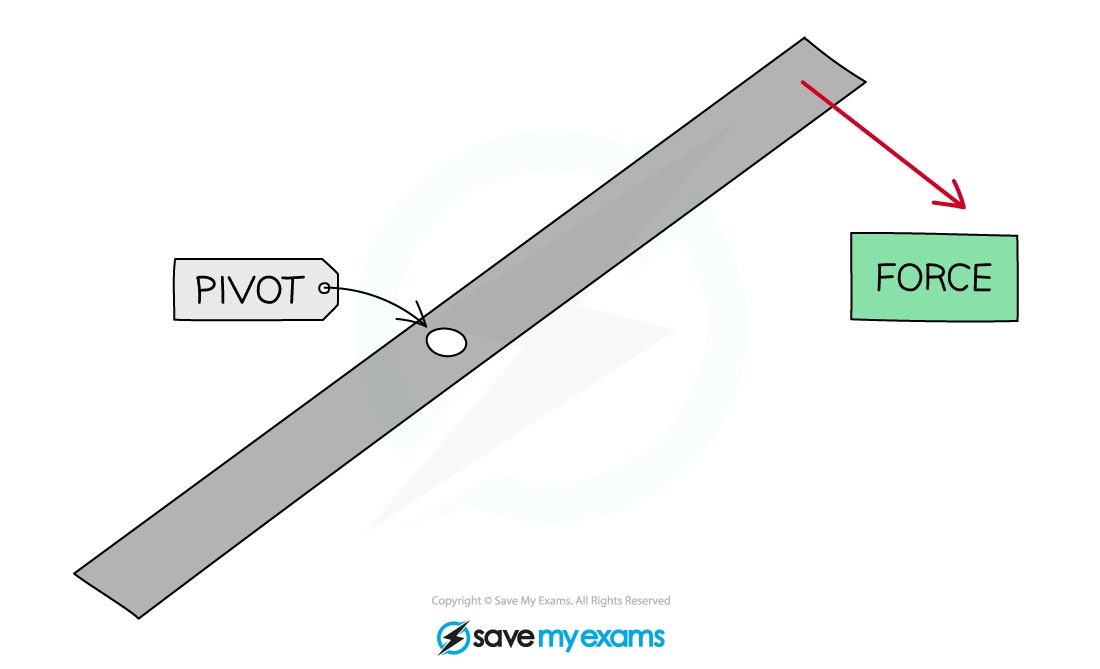
The force applied will cause the object to rotate clockwise about the pivot
The moment equation
A moment is defined as:
The turning effect of a force about a pivot
The size of a moment is defined by the equation:
The forces should be perpendicular to the distance from the pivot
For example, on a horizontal beam, the forces which will cause a moment are those directed upwards or downwards
The turning effect of a force exerted on a spanner
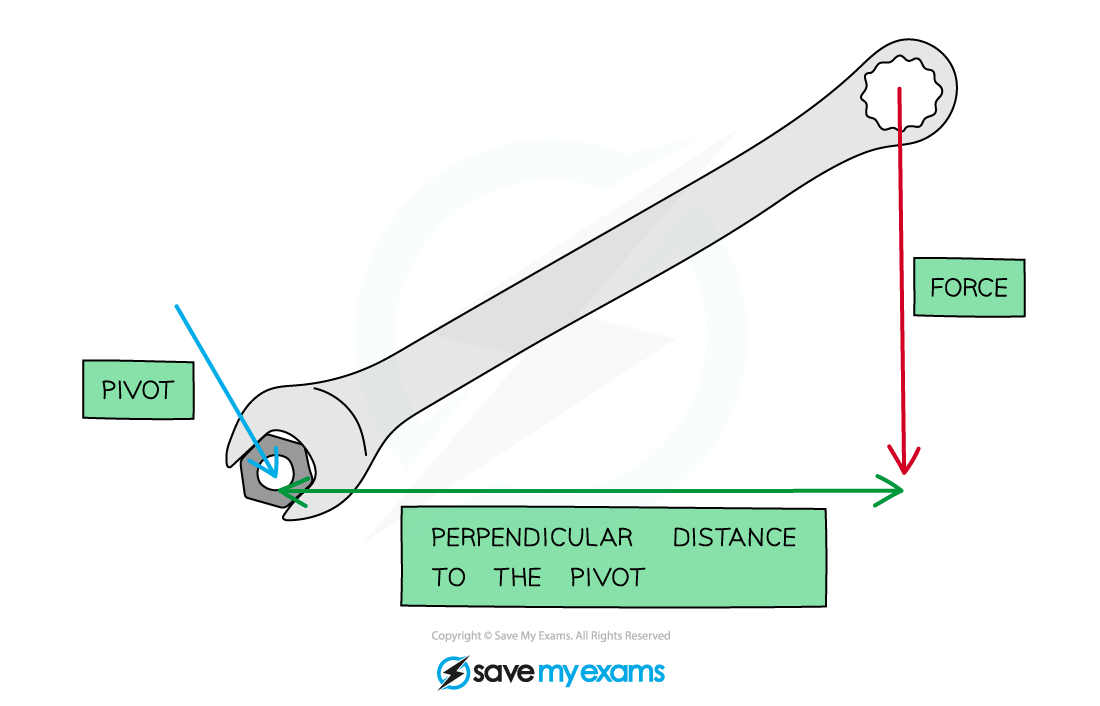
The moment depends on the force and perpendicular distance to the pivot
Increasing the distance at which a force is applied from a pivot decreases the force required
If you try to push open a door right next to the hinge, it is very difficult, as it requires a lot of force
If you push the door open at the side furthest from the hinge, then it is much easier, as less force is required
Forces required to open a door
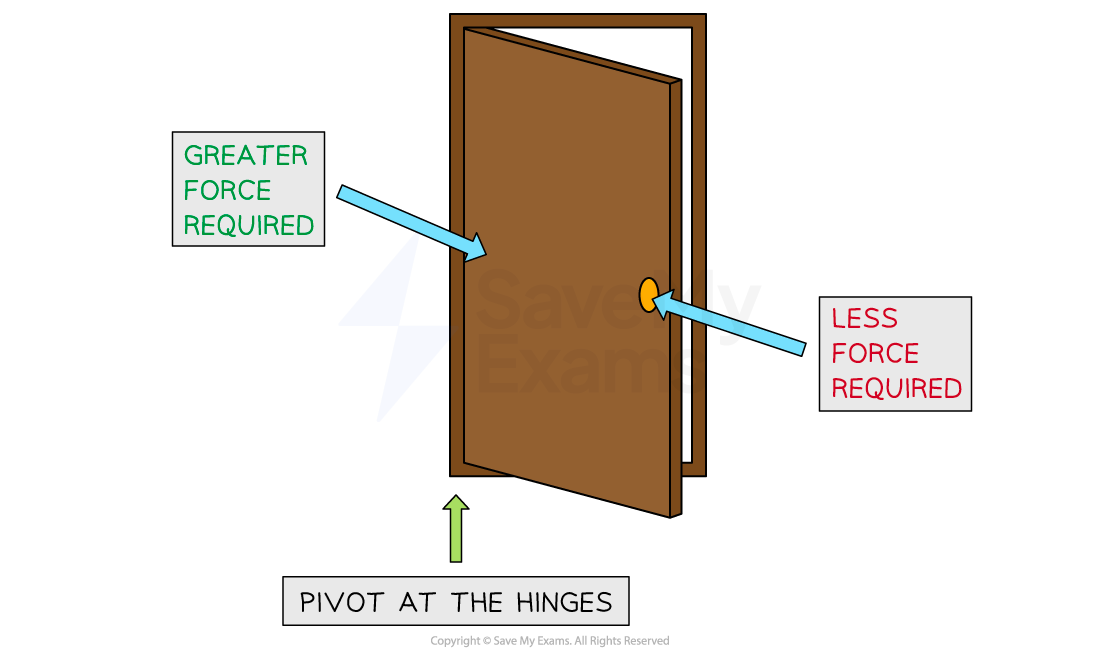
A greater force is required to push open a door next to the hinges than at the door handle
Worked Example
A carpenter attempts to loosen a bolt that has rusted. To turn the bolt, they exert a force of 22 N using a spanner of length 20 cm. The force is exerted 5 cm from the end of the spanner.
Calculate the turning effect of the force.
Answer:
Step 1: List the known quantities
Force,
Length of spanner,
Step 2: Determine the distance from the pivot
The force is exerted 5 cm from the end of the spanner
Therefore, the distance from the force to the pivot is
Convert cm to m
Step 3: Write out the equation for moments
Step 4: Substitute in the known values to calculate
Examiner Tips and Tricks
The moment of a force is measured in newton metres (N m), but can also be newton centimetres (N cm) if the distance is measured in cm instead.
If your IGCSE moments exam question doesn't ask for a specific unit, always convert the distance into metres
Principle of moments (core)
The principle of moments states that:
If an object is balanced, the total clockwise moment about a pivot equals the total anticlockwise moment about that pivot
The principle of moments means that for a balanced object, the moments on both sides of the pivot are equal
clockwise moment = anticlockwise moment
Principle of moments
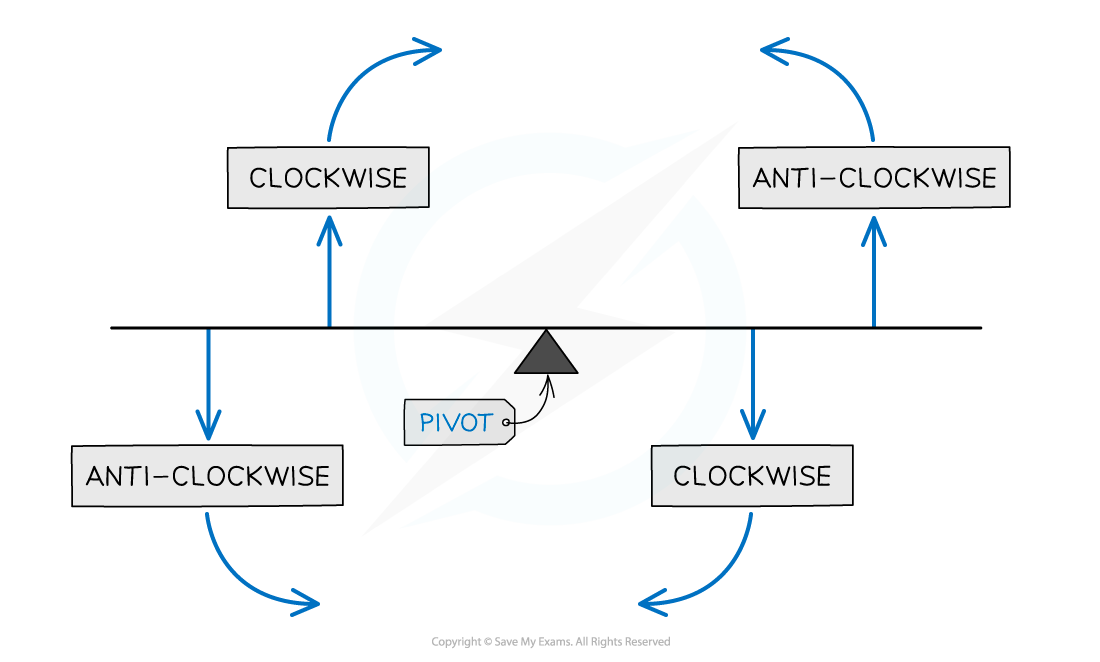
Imagine holding the beam about the pivot and applying just one of the forces. If the beam moves clockwise then the force applied is clockwise. This is the principle of moments
Worked Example
A parent and child are at opposite ends of a playground see-saw.
The weight force acting on the parent is 690 N and the weight force acting on the child is 140 N.
The adult sits at a distance of 0.3 m from the pivot.
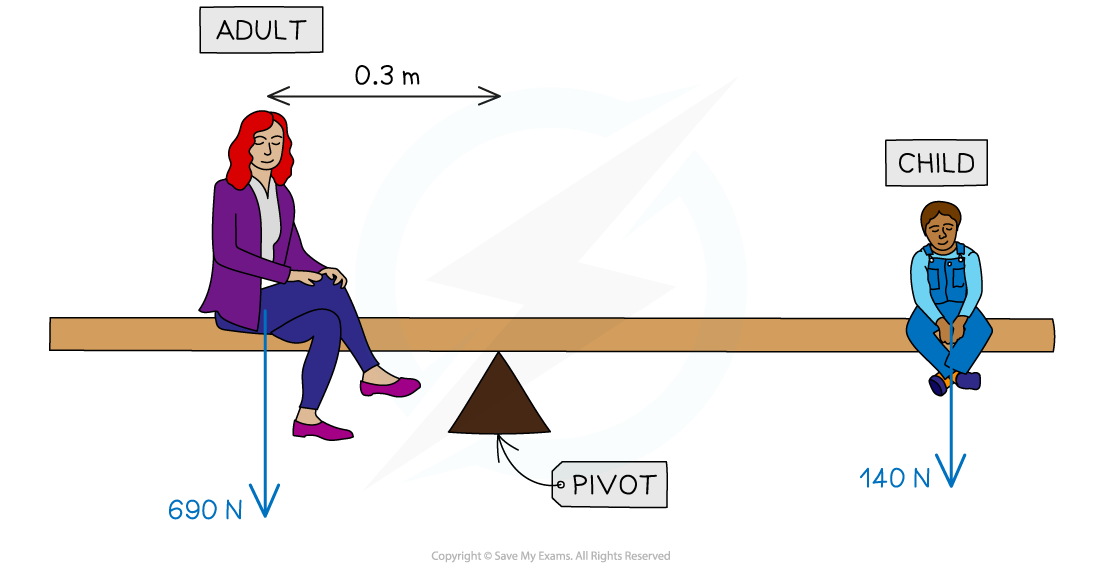
Calculate the distance the child must sit from the pivot for the see-saw to be balanced.
Use the principle of moments in your calculation.
Answer:
Step 1: List the known quantities
Clockwise force (child),
Anticlockwise force (adult),
Distance of adult from the pivot,
Step 2: Write down the moment equation and the principle of moments
Moment equation:
Principle of moments:
Step 3: Calculate the total clockwise moments
The clockwise moment is from the child
Step 4: Calculate the total anticlockwise moments
The anticlockwise moment is from the adult
Step 5: Substitute into the principle of moments equation
Step 6: Rearrange for the distance of the child from the pivot
The child must sit 1.5 m from the pivot to balance the see-saw
Examiner Tips and Tricks
Make sure that all the distances are in the same units and that you’re considering the correct forces as clockwise or anticlockwise
If you are studying the core tier for IGCSE Physics, you will only be expected to apply the principle of moments to a situation where one force acts on either side of the pivot
Principle of moments (extended)
Extended tier only
In the example below, the forces and distances of the objects on the beam are different, but they are arranged in a way that balances the whole system
Using the principle of moments
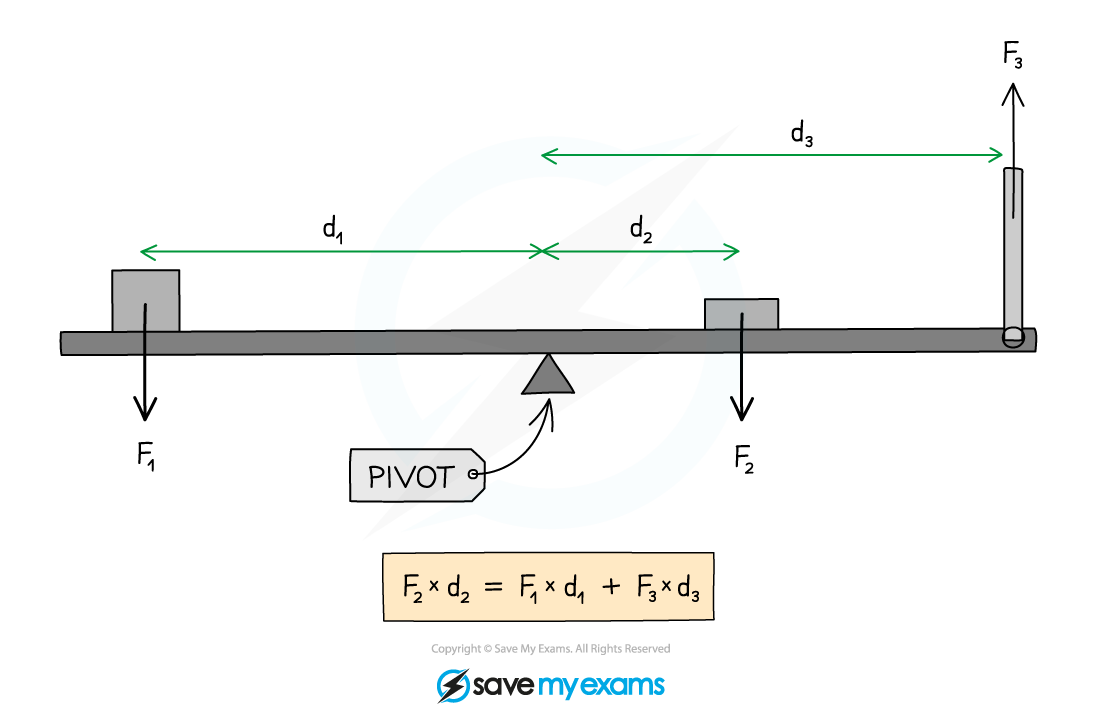
The clockwise and anticlockwise moments acting on a beam are balanced
In the above diagram:
Force
causes an anticlockwise moment of
about the pivot
Force
causes a clockwise moment of
about the pivot
Force
causes an anticlockwise moment of
about the pivot
Collecting the clockwise and anticlockwise moments:
Sum of the clockwise moments =
Sum of the anticlockwise moments =
Using the principle of moments, the beam is balanced when:
sum of the clockwise moments = sum of the anticlockwise moments

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

