Similar Areas & Volumes (Edexcel IGCSE Maths A) : Revision Note
Did this video help you?
Similar Areas & Volumes
What are similar shapes?
Two shapes are mathematically similar if one is an enlargement of the other
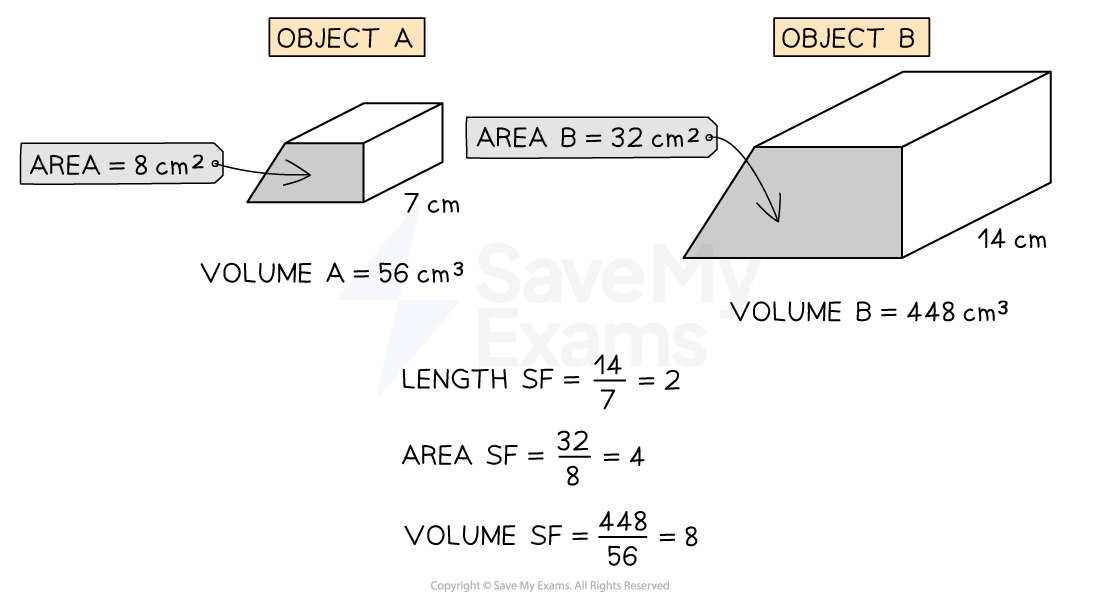
If the lengths of two similar shapes are linked by the scale factor, k
Equivalent areas are linked by an area factor, k2
Equivalent volumes are linked by a volume factor, k3
The scale factor (SF) for a given quantity (length, area or volume), can be found using the formula:
An object could be made either bigger or smaller by a scale factor
When k > 1, the object is getting bigger
This is also true for k2 > 1 and k3 > 1
When 0 < k < 1, the object is getting smaller
This is also true for 0< k2 < 1 and 0 < k3 < 1
How do I work with similar shapes involving area or volume?
STEP 1
Identify the equivalent known quantitiesRecognise if the quantities are lengths, areas or volumes
STEP 2
Find the scale factor from two known lengths, areas or volumesFor two lengths, k = length SF
For two areas, k2 = area SF
For two volumes, k3 = volume SF
STEP 3
Check the scale factorSF > 1 if getting bigger
0 < SF < 1 if getting smaller
STEP 4
If necessary, use the scale factor you have found to find other scale factorsIf you have the length scale factor
If you have the area scale factor
Find the volume scale factor by finding the length scale factor first
If you have the volume scale factor
Find the area scale factor by finding the length scale factor first
STEP 5
Multiply or divide by relevant scale factor to find a new quantity
Examiner Tips and Tricks
Take extra care not to mix up which shape is which when you have started carrying out the calculations
It can help to label the shapes and write an equation
Worked Example
Solid A and solid B are mathematically similar.
The volume of solid A is 32 cm3.
The volume of solid B is 108 cm3.
The height of solid A is 10 cm.
Find the height of solid B.
Calculate , the scale factor of enlargement for the volumes, using:
Or
Find the length scale factor by taking the cube root of the volume scale factor
Substitute the value for into formula for the heights of the similar shapes:
Height of B = 15 cm

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

