Translations (Edexcel IGCSE Maths A (Modular))
Revision Note
Written by: Dan Finlay
Reviewed by: Lucy Kirkham
Did this video help you?
Translations
What are transformations in maths?
There are four transformations to learn
translations, rotations, reflections and enlargements
A transformation can change the position, orientation and/or size of a shape
The original shape is called the object
The transformed shape is called the image
Vertices are labelled to show corresponding points
Vertices on the object are labelled A, B, C, etc.
Vertices on the image are labelled A’, B’, C’ etc.
What is a translation?
A translation moves a shape
The size and orientation (which way up it is) of the shape stays the same
The object and image are congruent
What is a translation vector?
The movement of a translation is described by a vector
You need to know how to write a translation using a vector (rather than words)
Vectors are written as column vectors in the form
where:
is the distance moved horizontally
Negative means move to the left
Positive means move to the right
is the distance moved vertically
Negative means move down
Positive means move up
How do I translate a shape?
STEP 1
Interpret the translation vector
means 3 to the right and 1 down
STEP 2
Move each vertex on the original object according to the vectorSTEP 3
Connect the new vertices and label the translated imageIt should look identical to the original object just in a different position
In some cases the image can overlap the object
How do I describe a translation?
To describe a translation, you must:
State that the transformation is a translation
Give the column vector that describes the movement
To find the vector:
Pick a point on the original shape
Identify the corresponding point on the image
Count how far left or right (
) you need to go from the object to get to the image
If you go to the left then
will be a negative number
Count how far up or down (
) you need to go from the object to get to the image
If you go down then
will be a negative number
Write these numbers as a vector
How do I reverse a translation?
To return a shape to its original position after a translation
the horizontal and vertical translations must both be reversed
The column vector to reverse a translation is simply the same as the original vector, but with the sign of both values changed
E.g. For a translation described by the column vector
The column vector for the reverse translation is
Examiner Tips and Tricks
The vector is how the shape moves not the size of the gap between the object and the image
Watch out for this common error!
Use tracing paper to check your answer
Worked Example
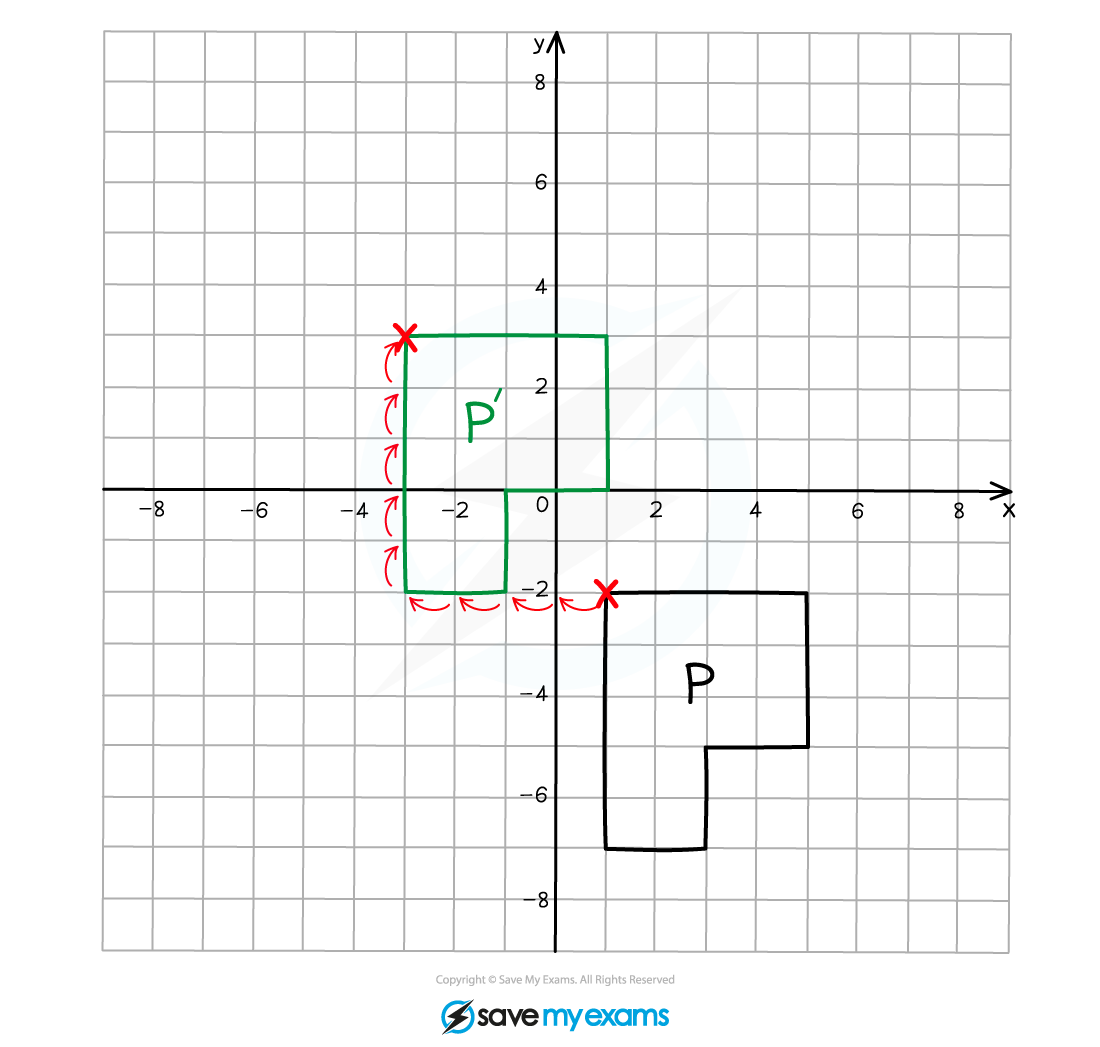
(a) On the grid below translate shape P using the vector .
Label your translated shape P'.
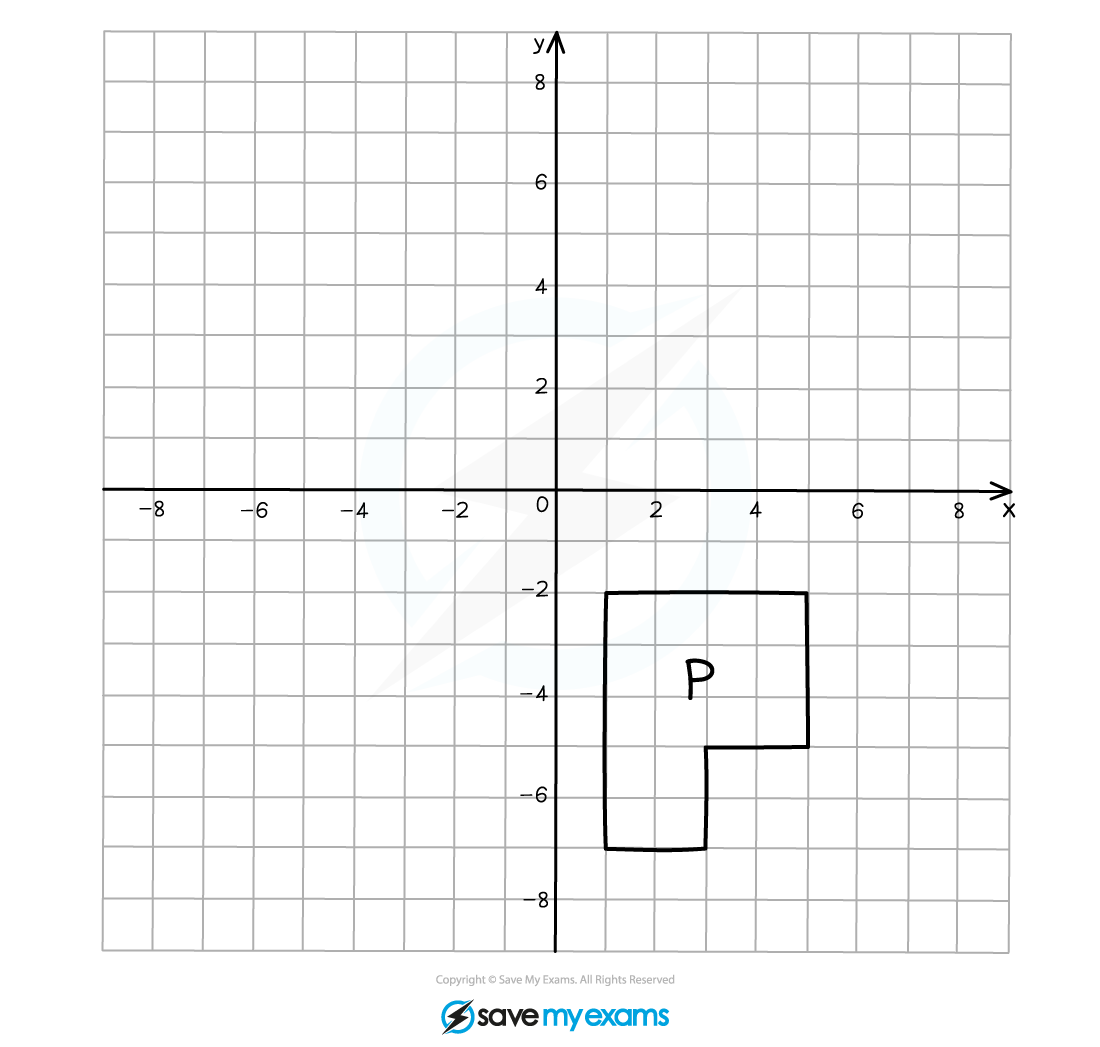
The vector means "4 to the left" and "5 up"
You don't have to draw in any arrows but it is a good idea to mark your paper after counting across and up a couple of times to check that you are in the correct place
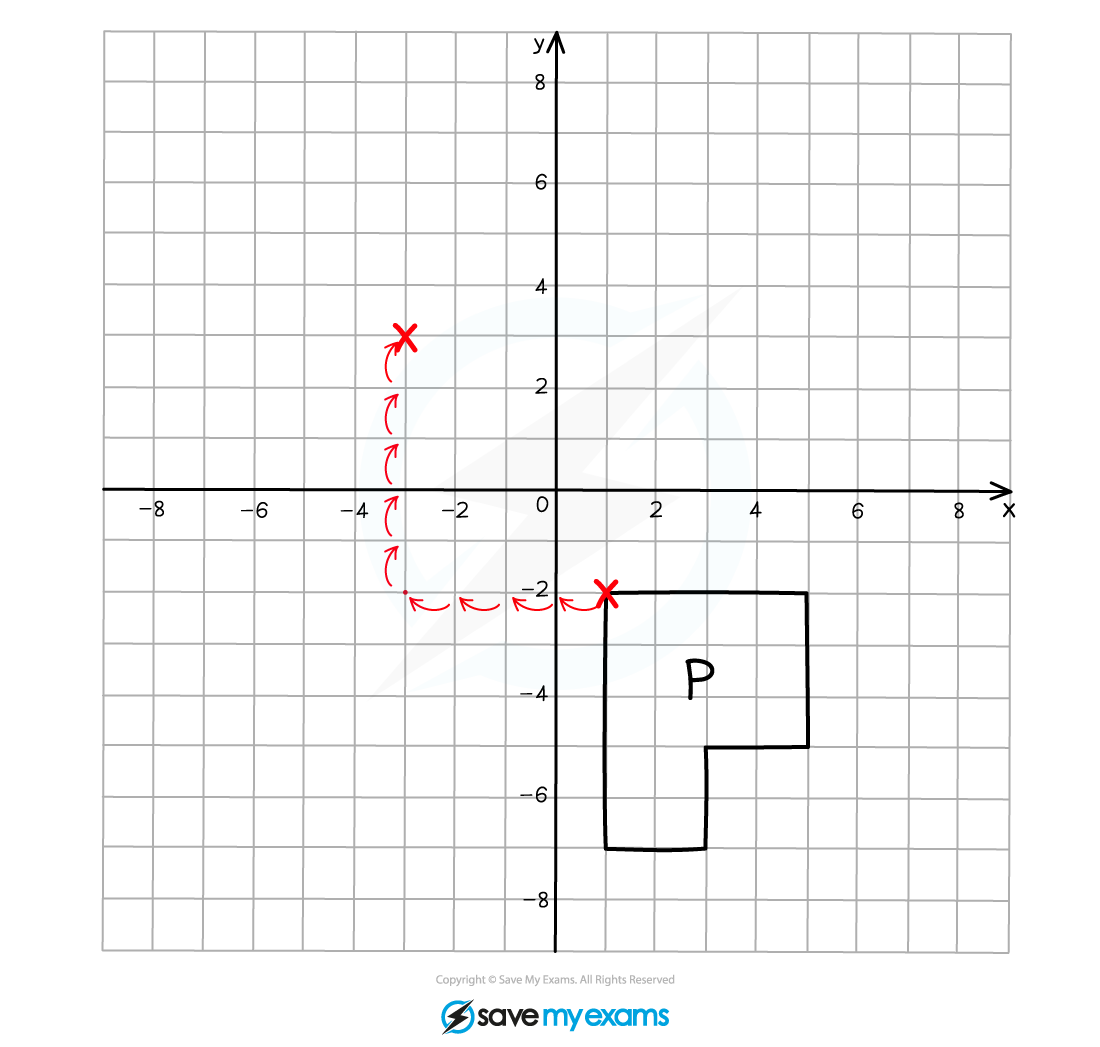
Translating one vertex and then following around the shape one vertex at a time makes it easier to get the shape in exactly the right position!
(b) Describe fully the single transformation that creates shape B from shape A.
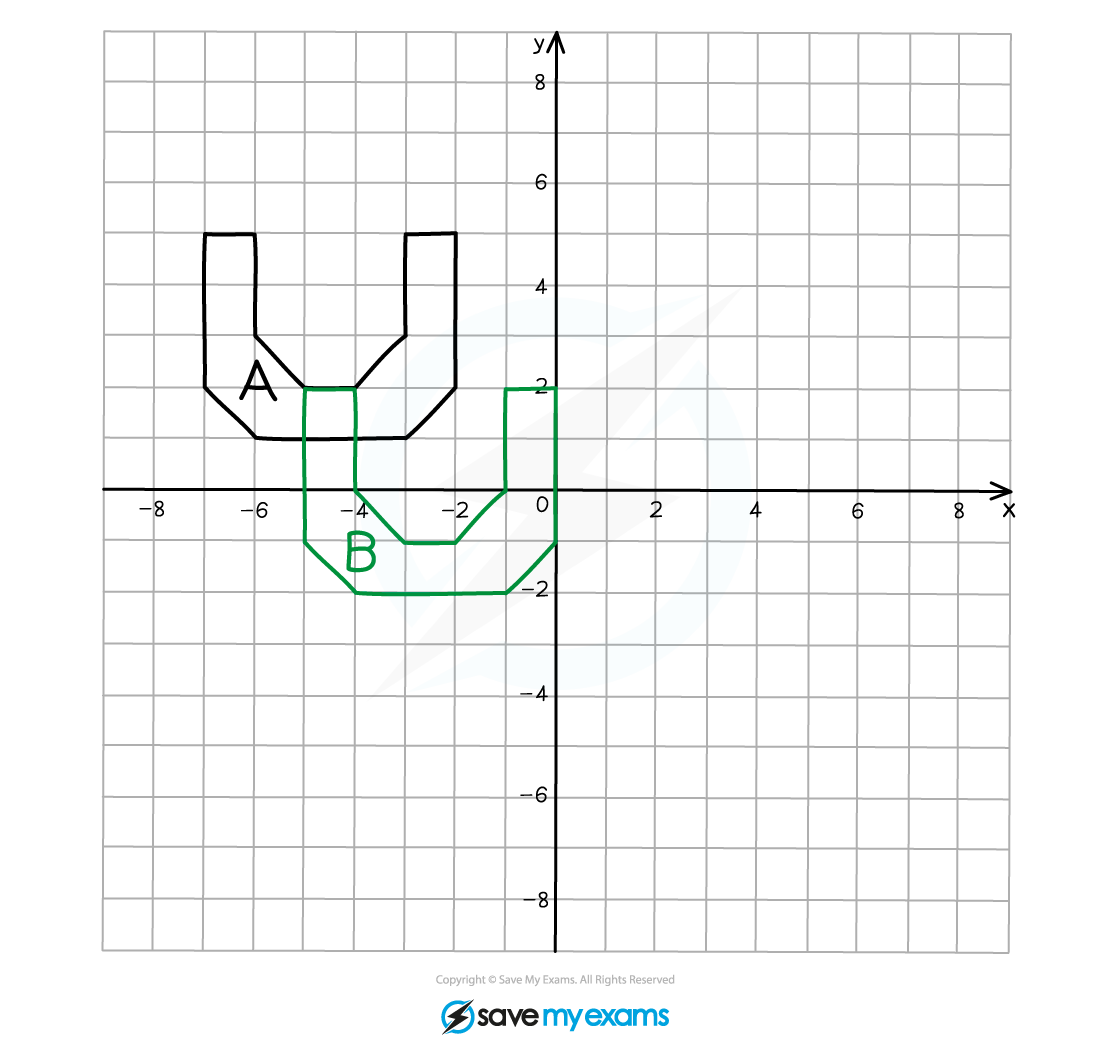
This is a case where the image overlaps the object
You should still see that the shape is the same size and the same way up so it is a translation
Start at a vertex on the original object that is well away from any overlap area to avoid confusion and count the number of position left/right and up/down that you need to move to reach the corresponding vertex on the translated image
Take care when counting around the axes!
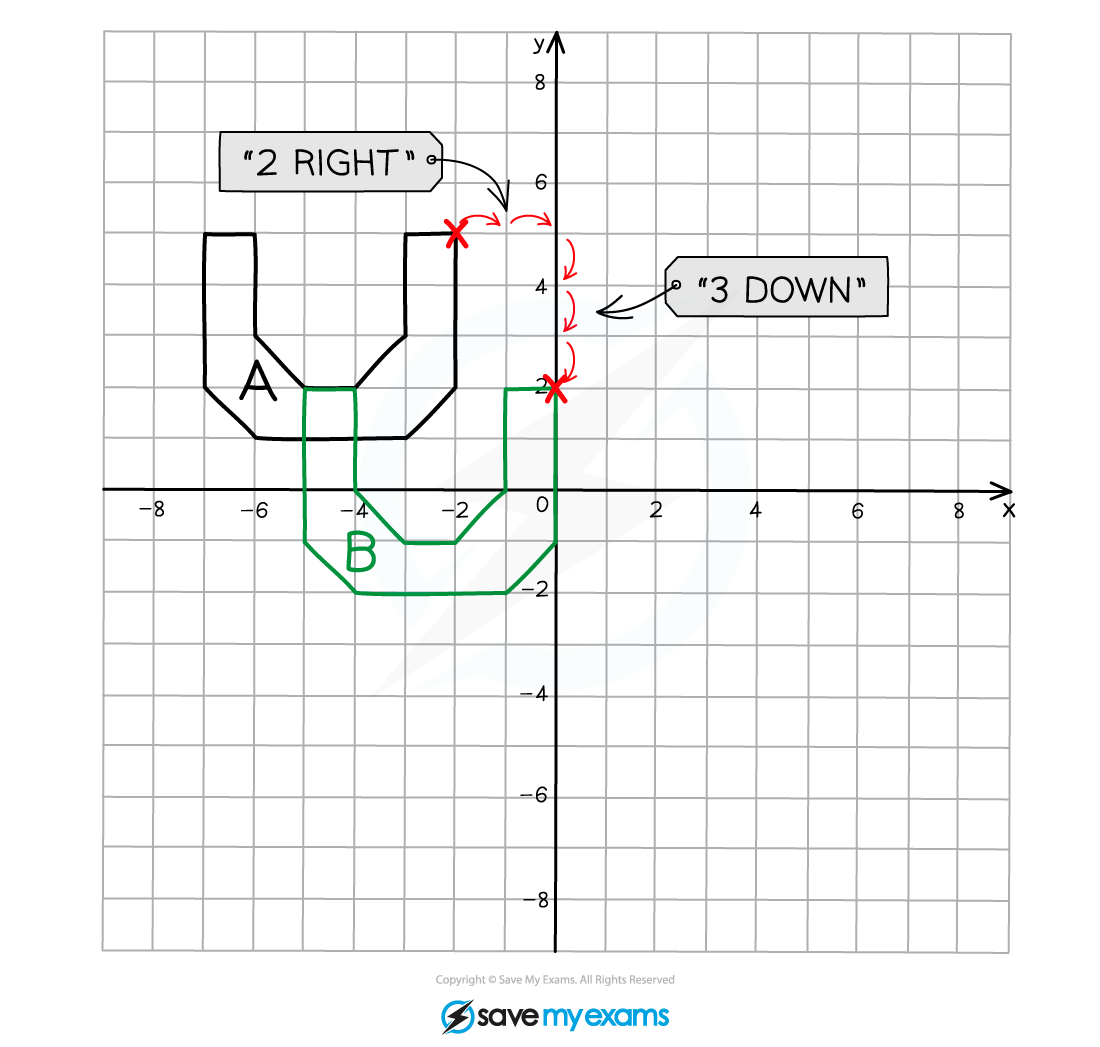
Shape A has been translated using the vector
(c) A shape has been translated from A to B using the translation vector .
Write down the vector used to reverse the translation from B to A.
To reverse the translation the shape must be moved in the opposite direction by the same amount
Reverse the signs in the translation vector
Last updated:

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

