Enlargements (Cambridge (CIE) IGCSE International Maths)

• To check that you have enlarged a shape correctly:

  • Draw lines going from the centre of enlargement to each of the vertices of the original shape

  • Extend these lines

  • The lines should go through the corresponding vertices of the enlarged image

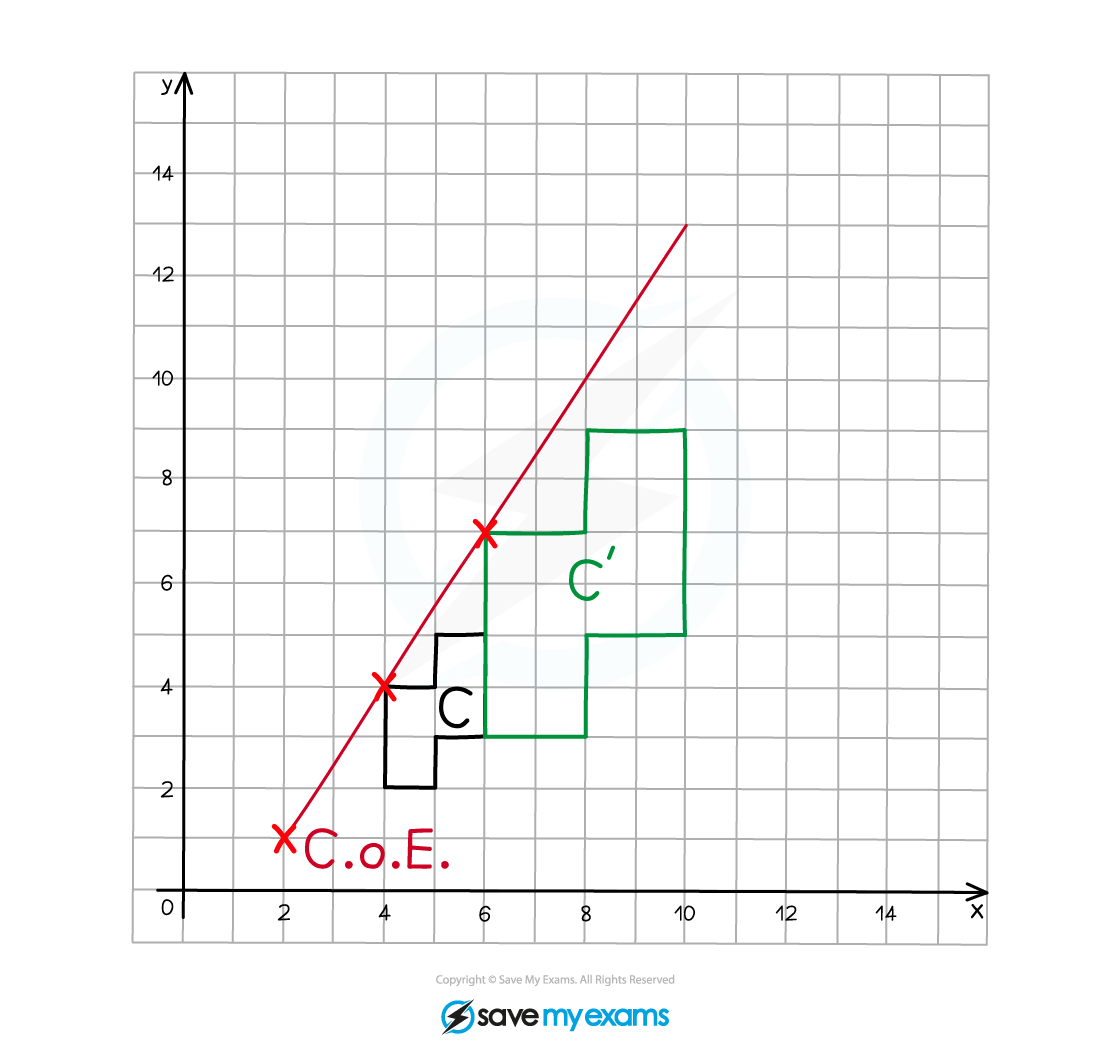
(a) On the grid below enlarge shape C using scale factor 2 and centre of enlargement (2, 1).

Label your enlarged shape C'.

Start by marking on the centre of enlargement (CoE)

Count the number of squares in both a horizontal and vertical direction to go from the CoE to one of the vertices on the original object, this is 2 to the right and 3 up in this example

As the scale factor is 2, multiply these distances by 2, so they become 4 to the right and 6 up

Count these new distances from the CoE to the corresponding point on the enlarged image and mark it on

Draw a line through the CoE and the pair of corresponding points, they should line up in a straight line

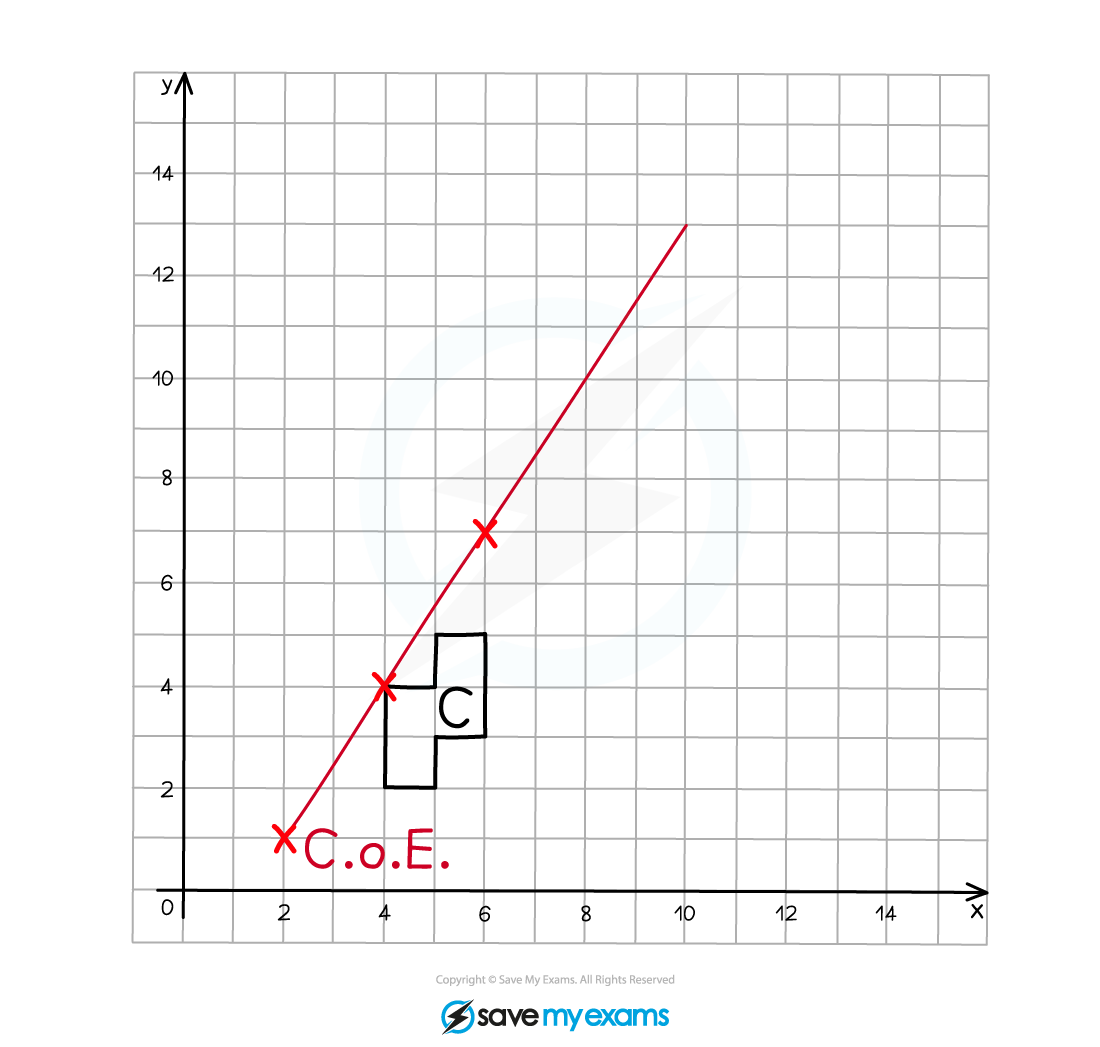
Repeat this process for each of the vertices on the original object (or at least 2)

Join adjacent vertices on the enlarged image as you go

Label the enlarged image C'

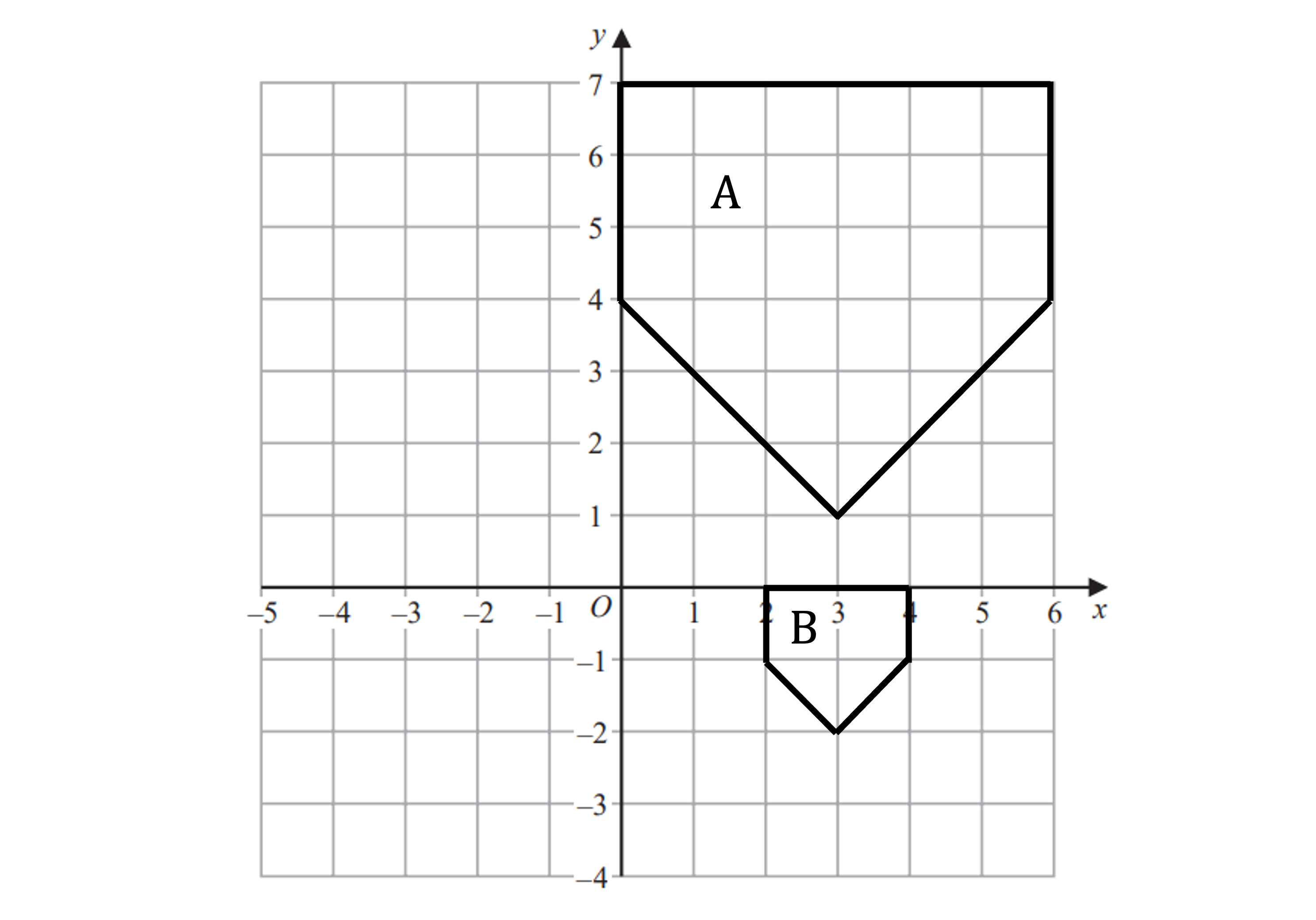
(b) Describe fully the single transformation that creates shape B from shape A.

We can see that the image is larger than the original object, therefore it must be an enlargement

As the enlarged image is bigger than the original object, the scale factor must be greater than 1

Compare two corresponding edges on the object and the image to find the scale factor

The height of the original "H" is 3 squares
The height of the enlarged "H" is 9 squares

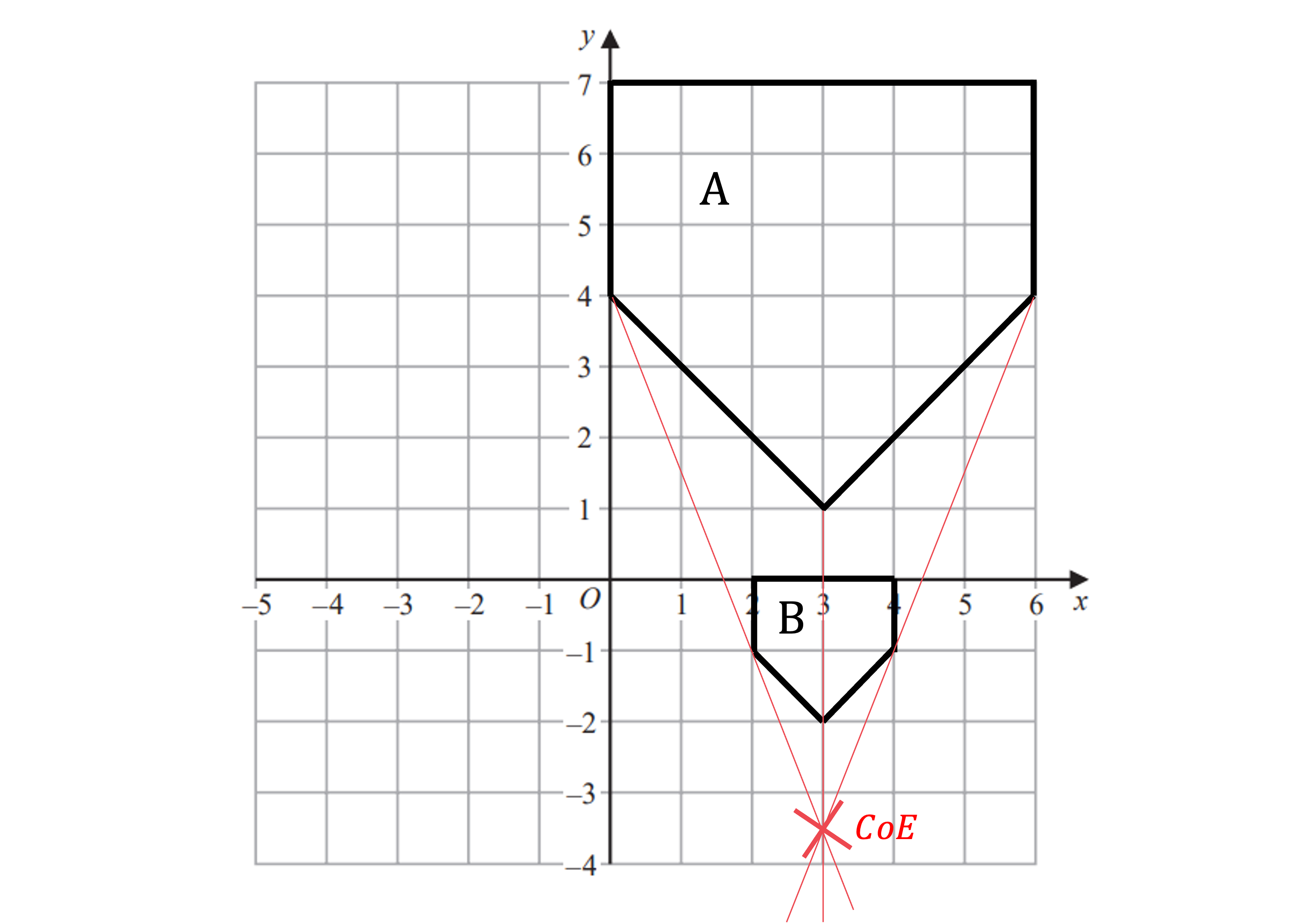
Draw a straight line through the CoE and a pair of corresponding points on the original object and the enlarged image

Repeat this step for as many vertices as you feel you need to so you can confidently locate the CoE
Do this for all pairs of vertices to be sure!

The point of intersection of the lines is the CoE

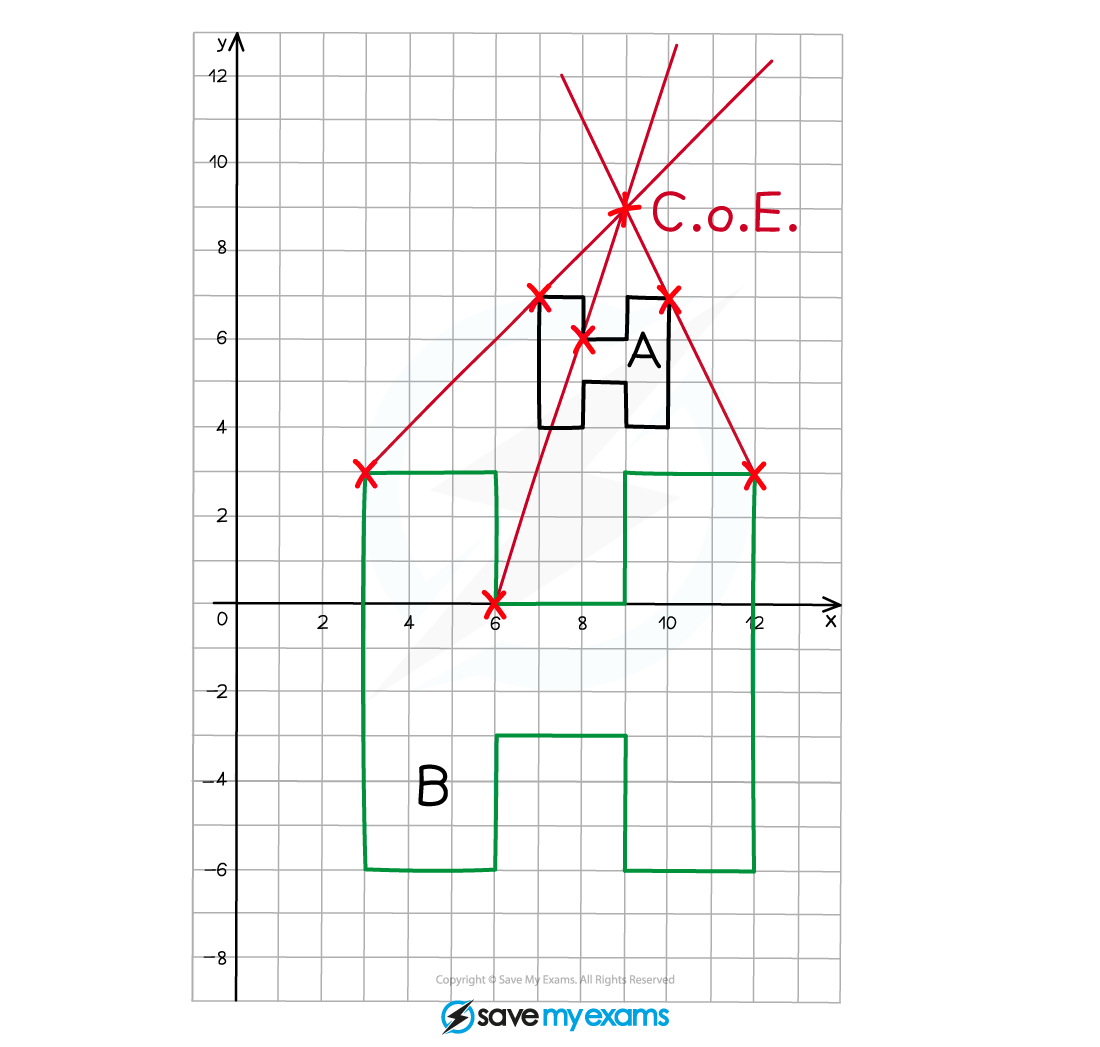
Shape A has been enlarged using a scale factor of 3 and a centre of enlargement (9, 9) to create shape B

(a) On the grid below enlarge shape C using scale factor  and centre of enlargement (4, 2).

Write down the four vertices of your enlarged shape.

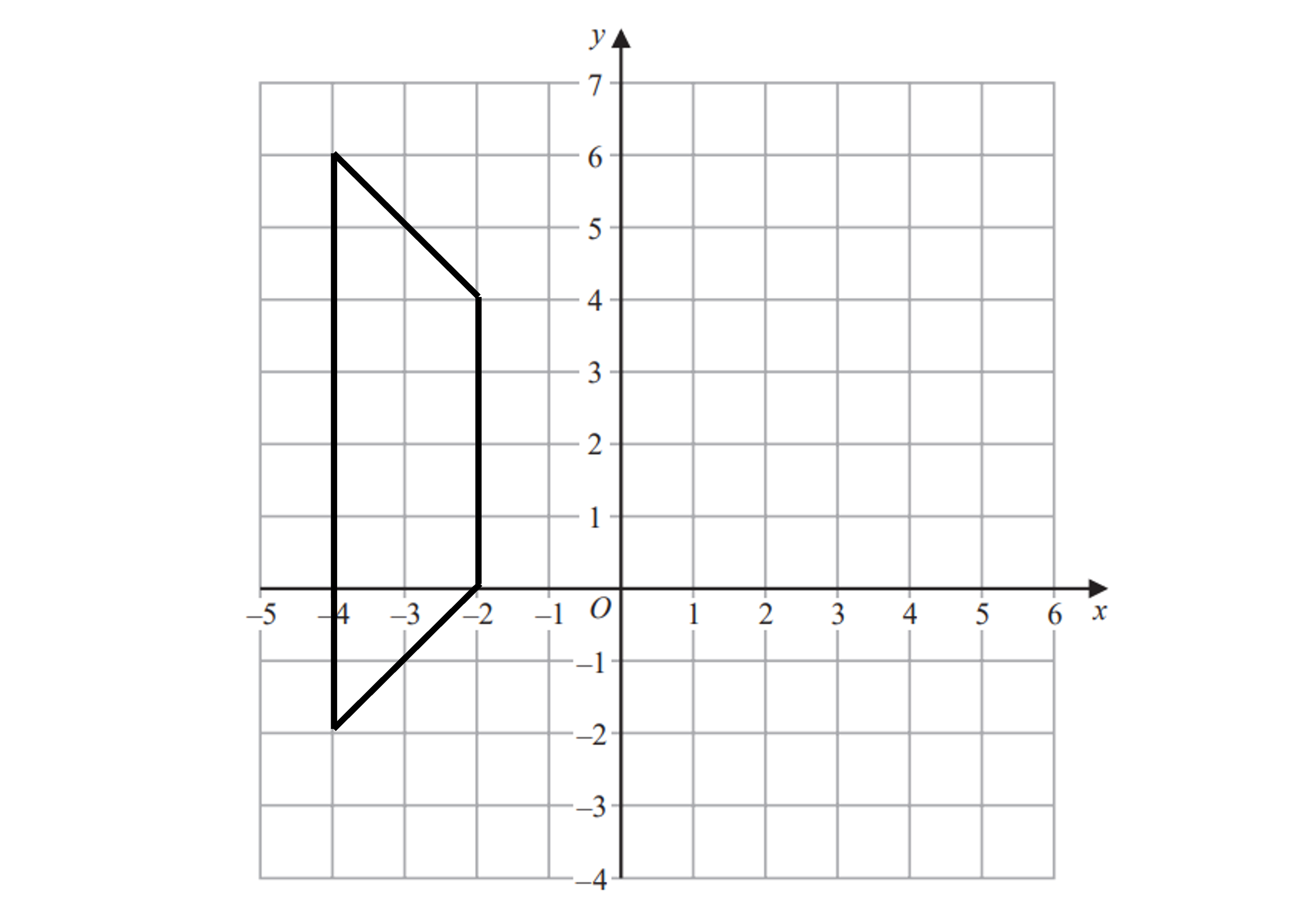
Mark the centre of enlargement at (4, 2)

Count the number of squares horizontally and vertically to any vertex - we've chosen the vertex at (-2, 4)

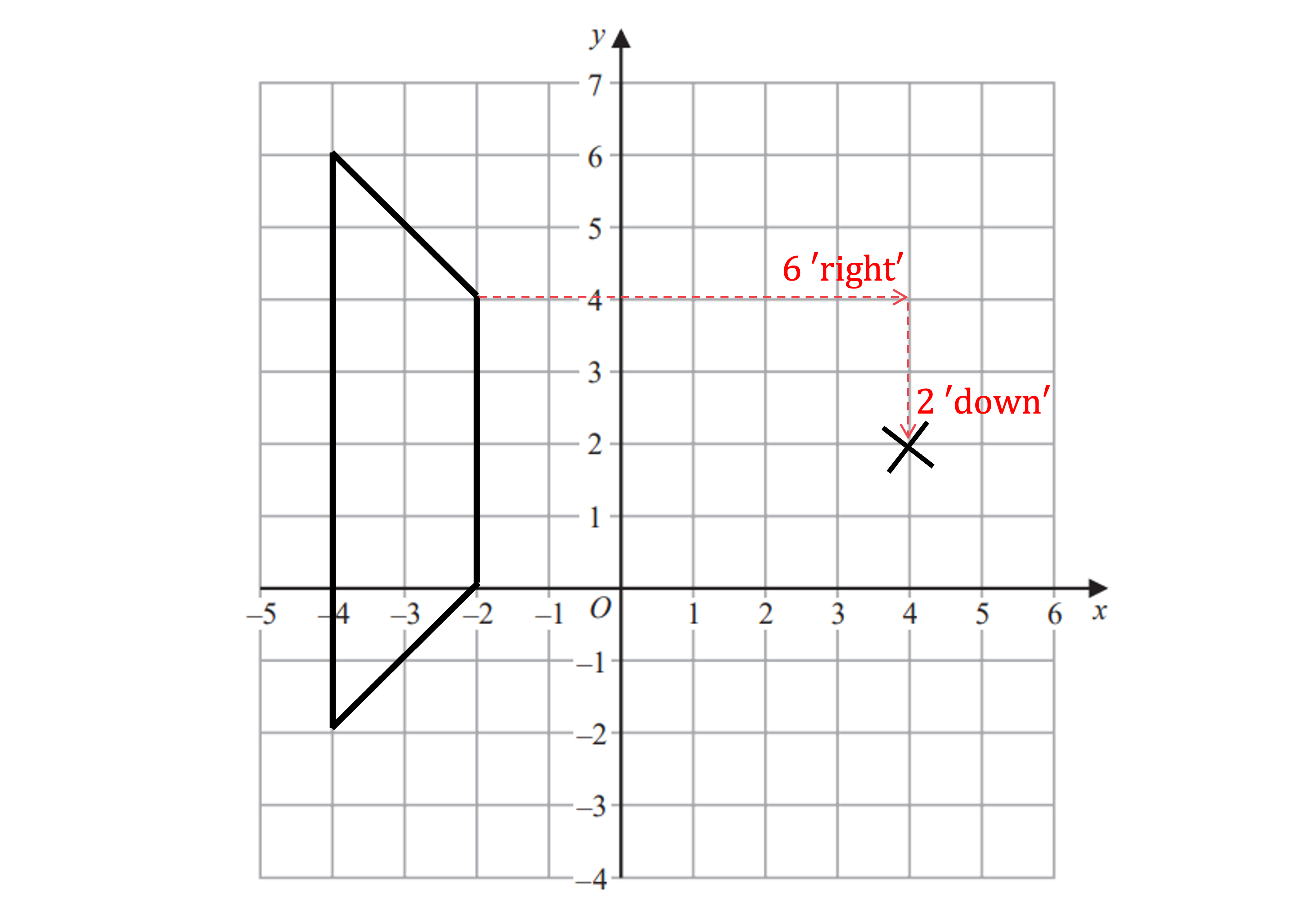
Multiply these distance by the scale factor, 

6 'right  'right'

2 'down'  'down'

Count these new distances (which should be smaller than the originals) from the CoE to find the corresponding point on the new image and mark it on

Repeat as required and draw lines through corresponding vertices and the CoE as a check

Use a logical order, working your way round the shape slowly, to ensure you do miss any vertices out

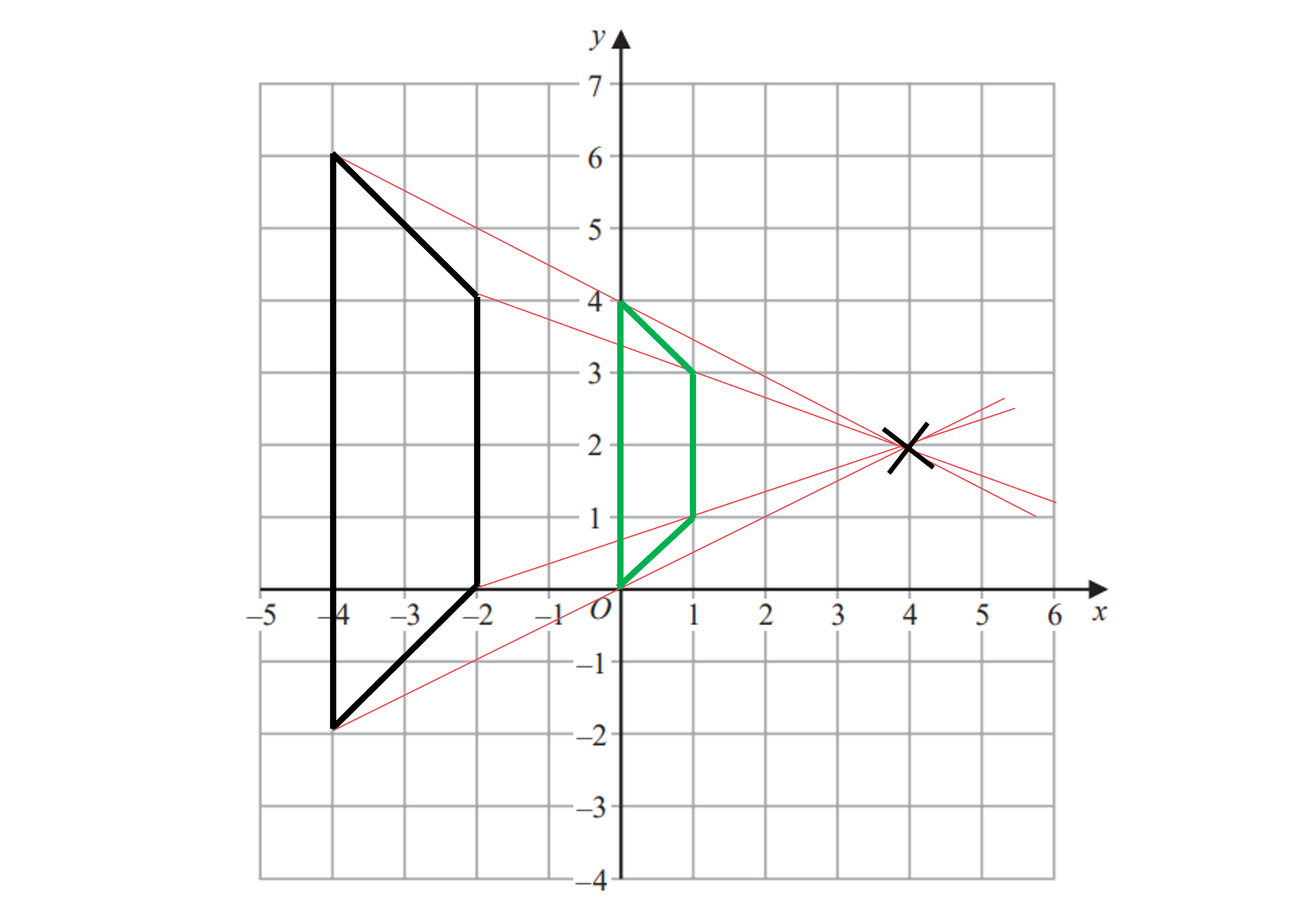
The four vertices of the enlarged shape are (0, 0), (0, 4),  (1, 3) and (1, 1)

(b) Describe fully the single transformation that creates shape B from shape A.

We can see the image is smaller than the original so it is a fractional enlargement

Compare two corresponding edges to find the scale factor - we've used the top edge

scale factor =

Draw straight lines through corresponding vertices on the original shape
Repeat this 3-4 times and you should find the lines intersect at the same point
This point will be the CoE

Shape A has been enlarged using a scale factor of and a centre of enlargement (3, -3.5) to create shape B

• Draw lines through the CoE and a vertex on the original object

  • this will remind you that the distances away from the CoE carry on in the opposite direction for a negative scale factor

• Watch out, exam questions are quite keen on combining both negative and fractional scale factors!

On the grid below enlarge shape F using scale factor    and centre of enlargement  . 

Label this shape F'.

If the area of F is 45 cm² write down the area of F'.

Start by marking the centre of enlargement (CoE) (6, -1) and selecting a starting vertex

Count the horizontal and vertical distances from the vertex to the CoE
Multiply those distances by the scale factor

Vertex at (-4, 3)

Distance to CoE from vertex on original object: 3 to the right and 3 up

Distances from CoE to corresponding vertex on enlarged image: to the right and  up

Count the new distances from the CoE, on the other side from the original object
Mark on the position of the corresponding point on the enlarged image

Draw a straight line through the corresponding vertices and the CoE to check that they line up

Repeat this process for each vertex in turn

Connect the vertices as you go around so that you don't forget which should connect to which

Remember, your enlarged image will be rotated by 180^o

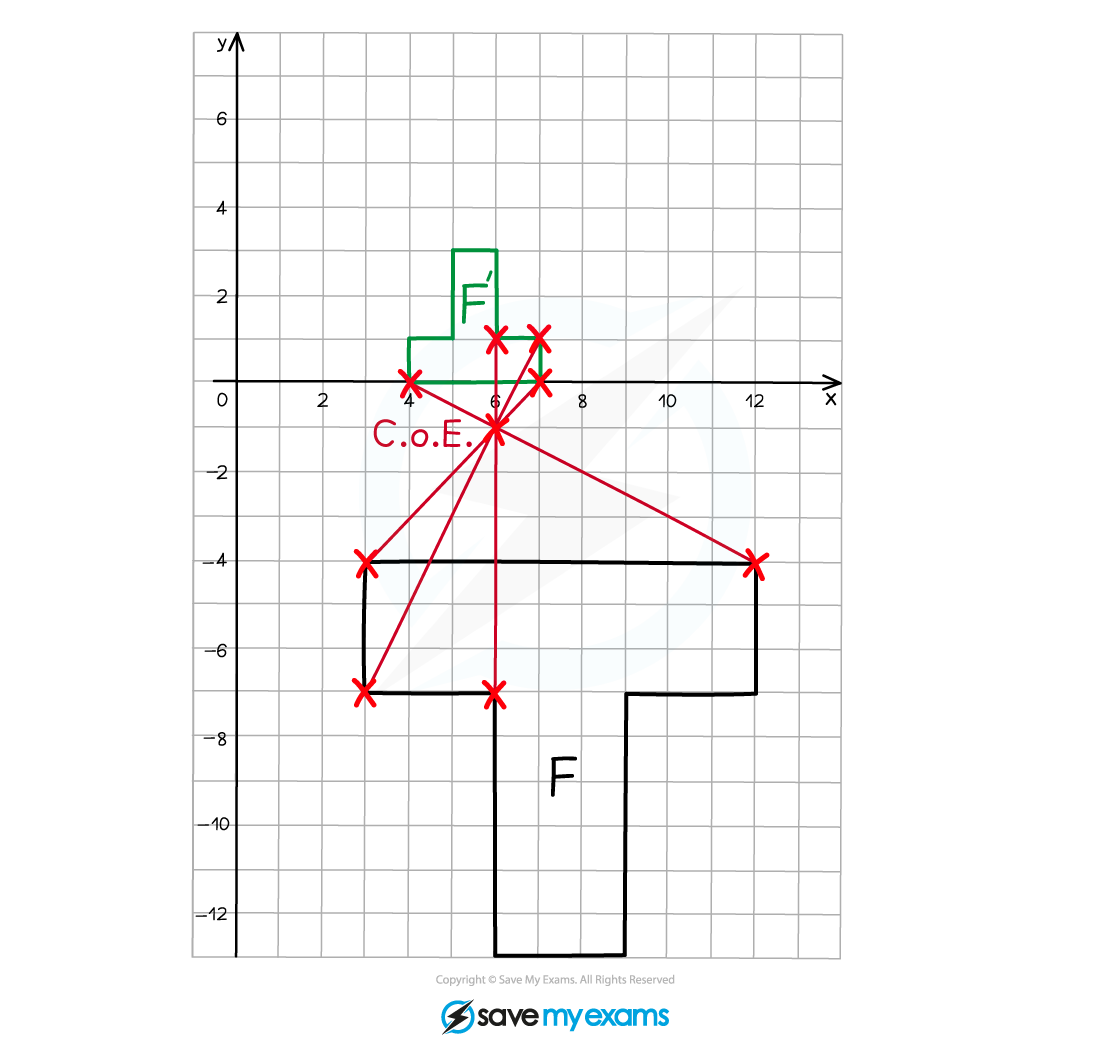
The length scale factor is  , meaning that each edge of the enlarged image is  the length of the corresponding edge on the original object

Find the area scale factor by squaring the length scale factor

Multiply the area of the original object by the area scale factor to find the area of the enlarged image