Basic Probability (Cambridge (CIE) IGCSE International Maths): Revision Note
Exam code: 0607
Did this video help you?
Basic probability
What is probability?
Probability describes the likelihood of something happening
In real-life you might use words such as impossible, unlikely and certain
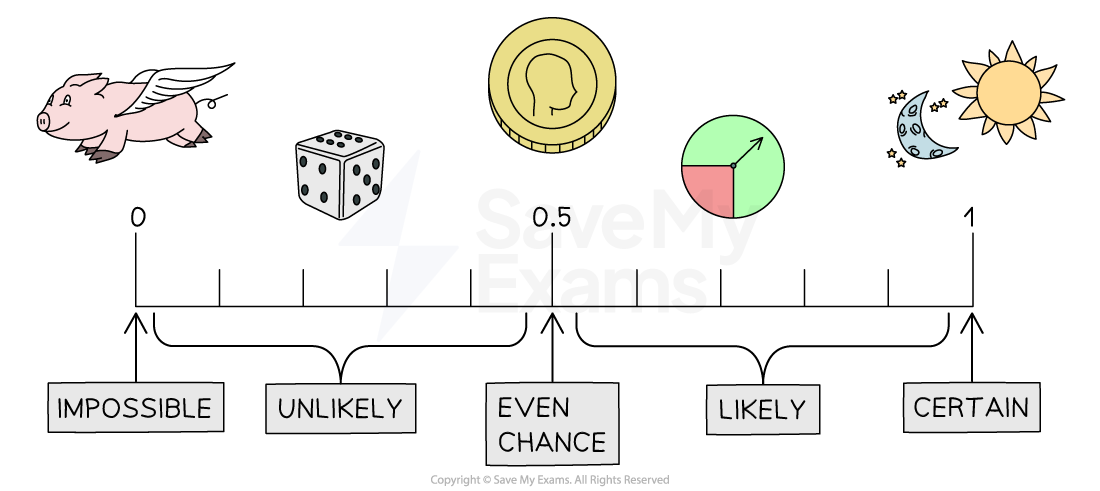
In maths we use the probability scale to describe probability
This means giving it a number between 0 and 1
0 means impossible
Between 0 and 0.5 means unlikely
0.5 means even chance
Between 0.5 and 1 means likely
1 means certain
Probabilities can be given as fractions, decimals or percentages
What key words and terminology are used in probability?
An experiment is an activity that is repeated to produce a set of results
Results can be observed (seen) or recorded
Each repeat is called a trial
An outcome is a possible result of a trial
An event is an outcome (or a collection of outcomes)
For example:
a dice lands on a six
a dice lands on an even number
Events are usually given capital letters
n(A) is the number of possible outcomes from event A
A = a dice lands on an even number (2, 4 or 6)
n(A) = 3
A sample space is the set of all possible outcomes of an experiment
It can be represented as a list or a table
The probability of event A is written P(A)
An event is said to be fair if there is an equal chance of achieving each outcome
If there is not an equal chance, the event is biased
For example, a fair coin has an equal chance of landing on heads or tails
How do I calculate basic probabilities?
If all outcomes are equally likely then the probability for each outcome is the same
The probability for each outcome is
If there are 50 marbles in a bag then the probability of selecting a specific one is
The theoretical probability of an event can be calculated by dividing the number of outcomes of that event by the total number of outcomes
This can be calculated without actually doing the experiment
If there are 50 marbles in a bag and 20 are blue, then the probability of selecting a blue marble is
How do I find missing probabilities?
The probabilities of all the outcomes add up to 1
If you have a table of probabilities with one missing, find it by making them all add up to 1
The complement of event A is the event where A does not happen
This can be thought of as not A
P(event does not happen) = 1 - P(event does happen)
For example, if the probability of rain is 0.3, then the probability of not rain is 1 - 0.3 = 0.7
What are mutually exclusive events?
Two events are mutually exclusive if they cannot both happen at once
When rolling a dice, the events “getting a prime number” and “getting a 6” are mutually exclusive
If A and B are mutually exclusive events, then the probability of either A or B happening is P(A) + P(B)
Complementary events are mutually exclusive
Examiner Tips and Tricks
If you are not told in the question how to leave your answer, then fractions are best for probabilities.
Worked Example
Emilia is using a spinner that has outcomes and probabilities as shown in the table.
Outcome | Blue | Yellow | Green | Red | Purple |
|---|---|---|---|---|---|
Probability |
| 0.2 | 0.1 |
| 0.4 |
The spinner has an equal chance of landing on blue or red.
(a) Complete the probability table.
The probabilities of all the outcomes should add up to 1
1 - 0.2 - 0.1 - 0.4 = 0.3
The probability that it lands on blue or red is 0.3
As the probabilities of blue and red are equal you can halve this to get each probability
0.3 ÷ 2 = 0.15
Now complete the table
Outcome | Blue | Yellow | Green | Red | Purple |
|---|---|---|---|---|---|
Probability | 0.15 | 0.2 | 0.1 | 0.15 | 0.4 |
(b) Find the probability that the spinner lands on green or purple.
As the spinner cannot land on green and purple at the same time they are mutually exclusive
This means you can add their probabilities together
0.1 + 0.4 = 0.5
P(Green or Purple) = 0.5
(c) Find the probability that the spinner does not land on yellow.
The probability of not landing on yellow is equal to 1 minus the probability of landing on yellow
1 - 0.2 = 0.8
P(Not Yellow) = 0.8

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?