IGCSEMathsCambridge (CIE)International MathsExtendedRevision NotesLengths, Areas & VolumesCongruence & SimilaritySimilar Lengths

Similar Lengths (Cambridge (CIE) IGCSE International Maths)

Revision Note

Naomi C

Written by: Naomi C

Reviewed by: Dan Finlay

Cambridge (CIE) International Maths: ExtendedEdexcel Maths A (Modular): Higher Unit 2Cambridge (CIE) International Maths: Core

Did this video help you?

Similar Lengths

How do I solve problems that involve similar lengths?

  • Equivalent lengths in two similar shapes will be in the same ratio and are linked by a scale factor

    • Identify known lengths of corresponding sides

    • Establish the type of enlargement

      • If the shape is getting bigger, then the scale factor is greater than 1

      • If the shape is getting smaller, then the scale factor is greater than 0 but less than 1

    • Find the scale factor 

      • Divide a known length on the second shape by the corresponding known length on the first shape

    • Use the scale factor to find the length you need

      • Multiply a known length by the scale factor on the first shape to find the corresponding length on the second shape

      • Divide a known length on the second shape by the scale factor to find the corresponding length on the first shape

Examiner Tips and Tricks

  • If similar shapes overlap on the diagram (or are not clear) draw them separately.

    • For example, in this diagram the triangles ABC and APQ are similar:

    Overlapping similar triangles

    • So redraw them separately before starting:

      Similar triangles sketched separately

Worked Example

ABCD and PQRS are similar shapes.
Find the length of PS.

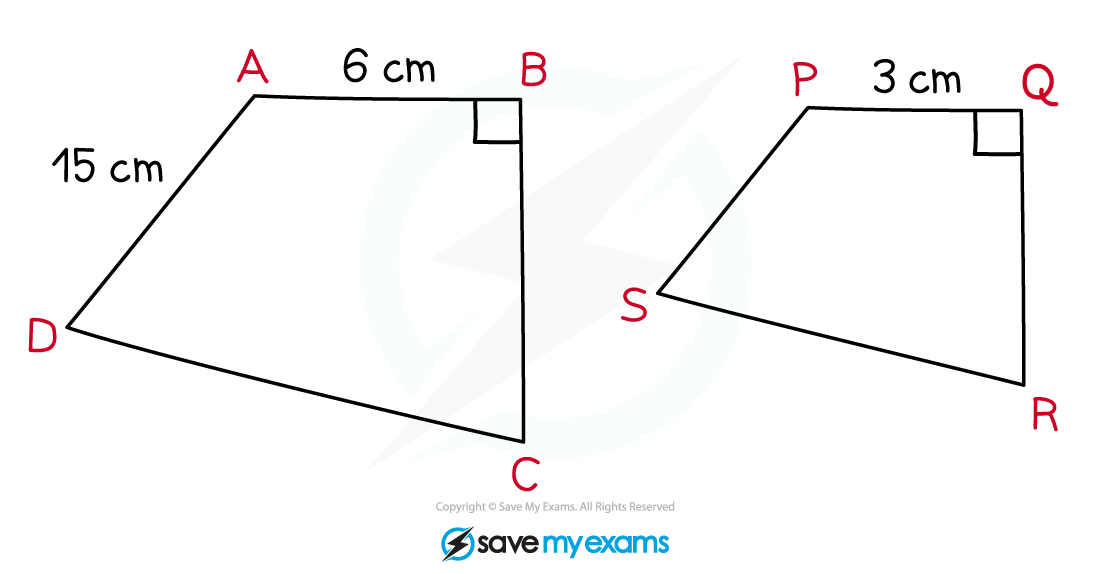
Two similar quadrilaterals

The two shapes are mathematically similar
Each length on the first shape can be multiplied by a scale factor to find the corresponding length on the second shape

Identify two known corresponding sides of the similar shapes

AB  and PQ  are corresponding sides

The second shape is smaller than the first shape so the scale factor will be between 0 and 1 
Divide the known length on the second shape by the corresponding length on the first shape to find the scale factor

table row cell Scale space Factor space end cell equals cell 3 over 6 equals 1 half end cell end table

Multiply the length AD  by the scale factor to find its corresponding length PS  on the second shape

table attributes columnalign right center left columnspacing 0px end attributes row cell P S space end cell equals cell 1 half cross times 15 equals 15 over 2 end cell row blank blank blank end table

bold italic P bold italic S bold space bold equals bold space bold 7 bold. bold 5 bold space bold cm

Last updated:

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Did this page help you?

    Previous:SimilarityNext:Similar Areas & Volumes
    Author
    Reviewer
    Naomi C

    Author: Naomi C

    Expertise: Maths

    Naomi graduated from Durham University in 2007 with a Masters degree in Civil Engineering. She has taught Mathematics in the UK, Malaysia and Switzerland covering GCSE, IGCSE, A-Level and IB. She particularly enjoys applying Mathematics to real life and endeavours to bring creativity to the content she creates.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.