Introduction to Sequences (Cambridge (CIE) IGCSE International Maths) : Revision Note
Did this video help you?
Introduction to Sequences
What are sequences?
A sequence is an ordered set of numbers that follow a rule
For example 3, 6, 9, 12...
The rule is to add 3 each time
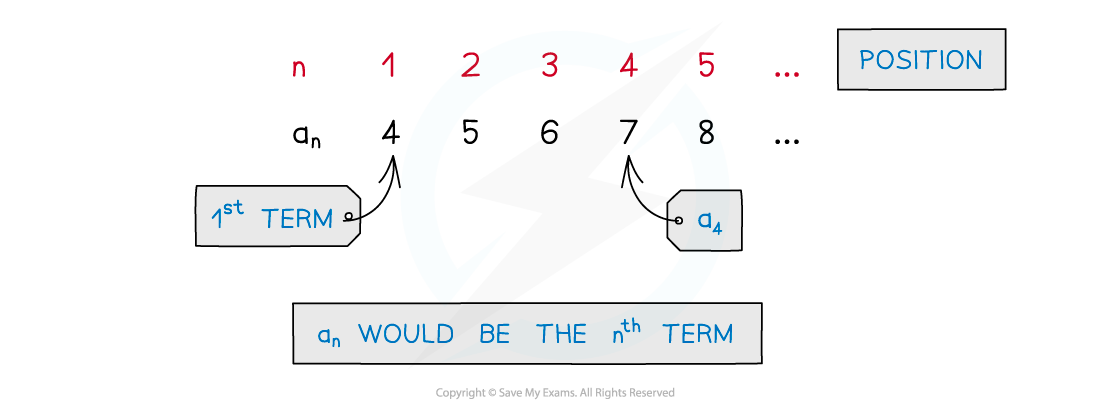
Each number in a sequence is called a term
The location of a term within a sequence is called its position
The letter n is used for position
n = 1 refers to the 1st term
n = 2 refers to the 2nd term
If you do not know its position, you can say the n th term
Another way to show the position of a term is using subscripts
A general sequence is given by a1, a2, a3, ...
a1 represents the 1st term
a2 represents the 2nd term
an represents the nth term
How do I write out a sequence using a term-to-term rule?
Term-to-term rules tell you how to get the next term from the term you are on
It is what you do each time
For example, starting on 4, add 10 each time
4, 14, 24, 34, ...
How do I write out a sequence using a position-to-term rule?
A position-to-term rule is an algebraic expression in n that lets you find any term in the sequence
This is also called the n th term formula
You need to know what position in the sequence you are looking for
To get the 1st term, substitute in n = 1
To get the 2nd term, substitute in n = 2
You can jump straight to the 100th term by substituting in n = 100
You do not need to find all 99 previous terms
For example, the n th term is 8n + 2
The 1st term is 8×1 + 2 = 10
The 2nd term is 8×2 + 2 = 18
The 100th term is 8×100 + 2 = 802
How do I know if a value belongs to a sequence?
If you know the n th term formula, set the value equal to the formula
This creates an equation to solve for n
For example, a sequence has the n th term formula 8n + 2
Is 98 in the sequence?
It is in the sequence, it is the 12th term
Is 124 in the sequence?
n is not a whole number, so it is not in the sequence
Examiner Tips and Tricks
In the exam, it helps to write the position number (the value of n) above each term in the sequence.
Worked Example
A sequence has the n th term formula 3n + 2.
(a) Find the first three terms in the sequence.
Substitute n = 1, n = 2 and n = 3 into the formula
3×1 + 2 = 5
3×2 + 2 = 8
3×3 + 2 = 11
5, 8, 11
(b) Find the 80th term.
Substitute n = 80 into the formula
3×80 + 2
The 80th term is 242
(c) Determine whether the number 96 is in the sequence.
Set the formula equal to 96
Solve to find n
If n is a whole number, it is a term in the sequence
94 is not divisible by 3
The nearest possible value is 95 ((95-2) ÷ 3 = 31, the 31st term)
96 is not in the sequence

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

