Interpreting Histograms (Cambridge (CIE) IGCSE Maths)

Revision Note

Test yourself Flashcards

Written by: Roger B

Reviewed by: Dan Finlay

Did this video help you?

Interpreting Histograms

How do I interpret a histogram?

It is important to remember that the frequency density (y-) axis does not tell us frequency
- The area of the bar is equal to the frequency
  - $\begin{array}{rcl} frequency & = & frequency density \times class width \end{array}$
Note that a very simple histogram may have equal class widths
- In this case the y-axis may be labelled 'frequency' instead of 'frequency density'
- If 'frequency' is on the y-axis, then you can use the heights of the bars to directly determine the frequencies

You may be asked to estimate the frequency of part of a bar/class interval within a histogram
- Find the area of the bar for the part of the interval required
- Once area is known, frequency can be found as above
You can use histograms for two data sets to compare the data distributions
- but only if they have the same class intervals and the same frequency density scales

Examiner Tips and Tricks

The frequency density axis will not always be labelled
- Look carefully at the scale, it is unlikely to be 1 unit to 1 square

Worked Example

The table below and the corresponding histogram show the weight, in kg, of some newborn bottlenose dolphins.

Weight w kg	Frequency
4 ≤ w < 8	4
8 ≤ w < 10	16
10 ≤ w < 12	19
12 ≤ w < 15	12
15 ≤ w < 30

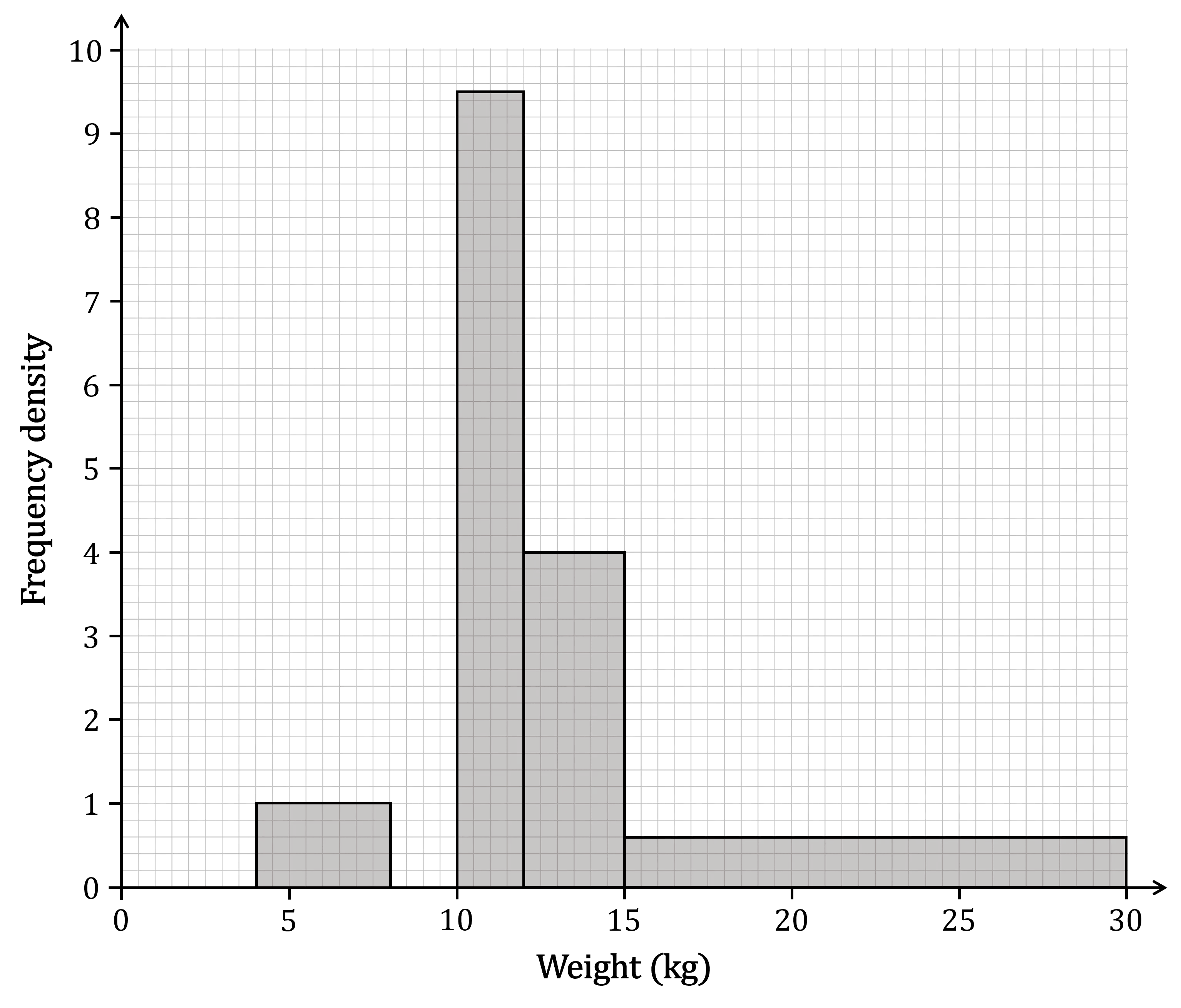
A partially complete histogram for the data in the question.

(a) Use the histogram to complete the table.

The frequency for the 15 ≤ w < 30 class interval is missing

The bar for that class interval on the histogram has a

height (frequency density) of 0.6
width of 30-15 = 15

Rearrange $frequency density = \frac{frequency}{class width}$ to get

$frequency = frequency density \times class width$

$frequency = 0.6 \times 15 = 9$

Weight w kg	Frequency
4 ≤ w < 8	4
8 ≤ w < 10	16
10 ≤ w < 12	19
12 ≤ w < 15	12
15 ≤ w < 30	9

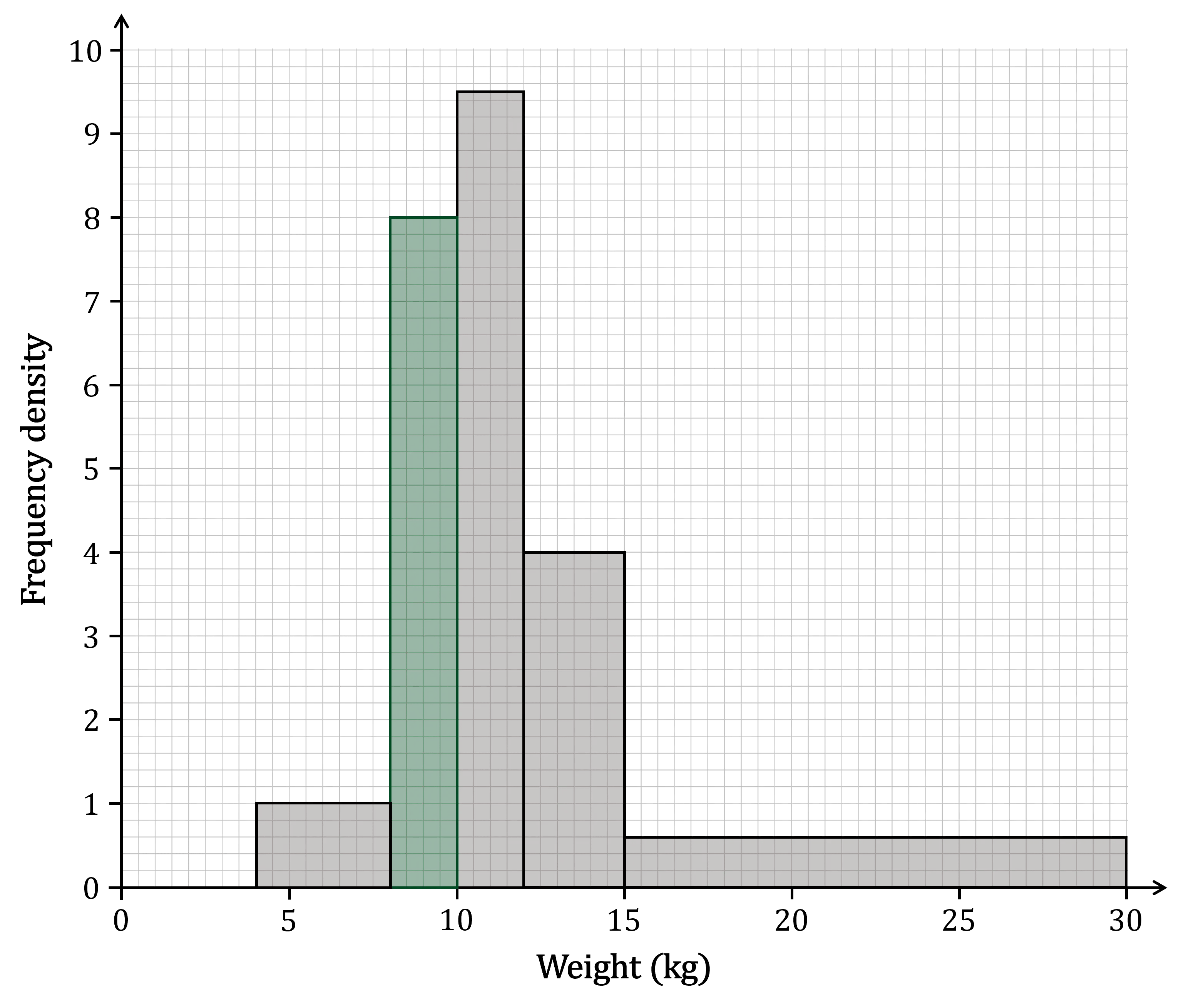
(b) Use the table to complete the histogram.

The bar for the 4 ≤ w < 8 class interval is missing

That class interval has a

frequency of 16
width of 10-8 = 2

Use $frequency density = \frac{frequency}{class width}$ to find the frequency density

$frequency density = \frac{16}{2} = 8$

Draw a bar with that height on the histogram, between 8 and 10 on the horizontal axis

A completed histogram for the data in the question.

We know from part a) that there are 9 dolphins in the 15 ≤ w < 30 class interval
So we need to estimate the number of dolphins that are in the interval 13 ≤ w < 15

For 13 ≤ w < 15, the histogram shows that

the frequency density is 4
the width is 15-13 = 2

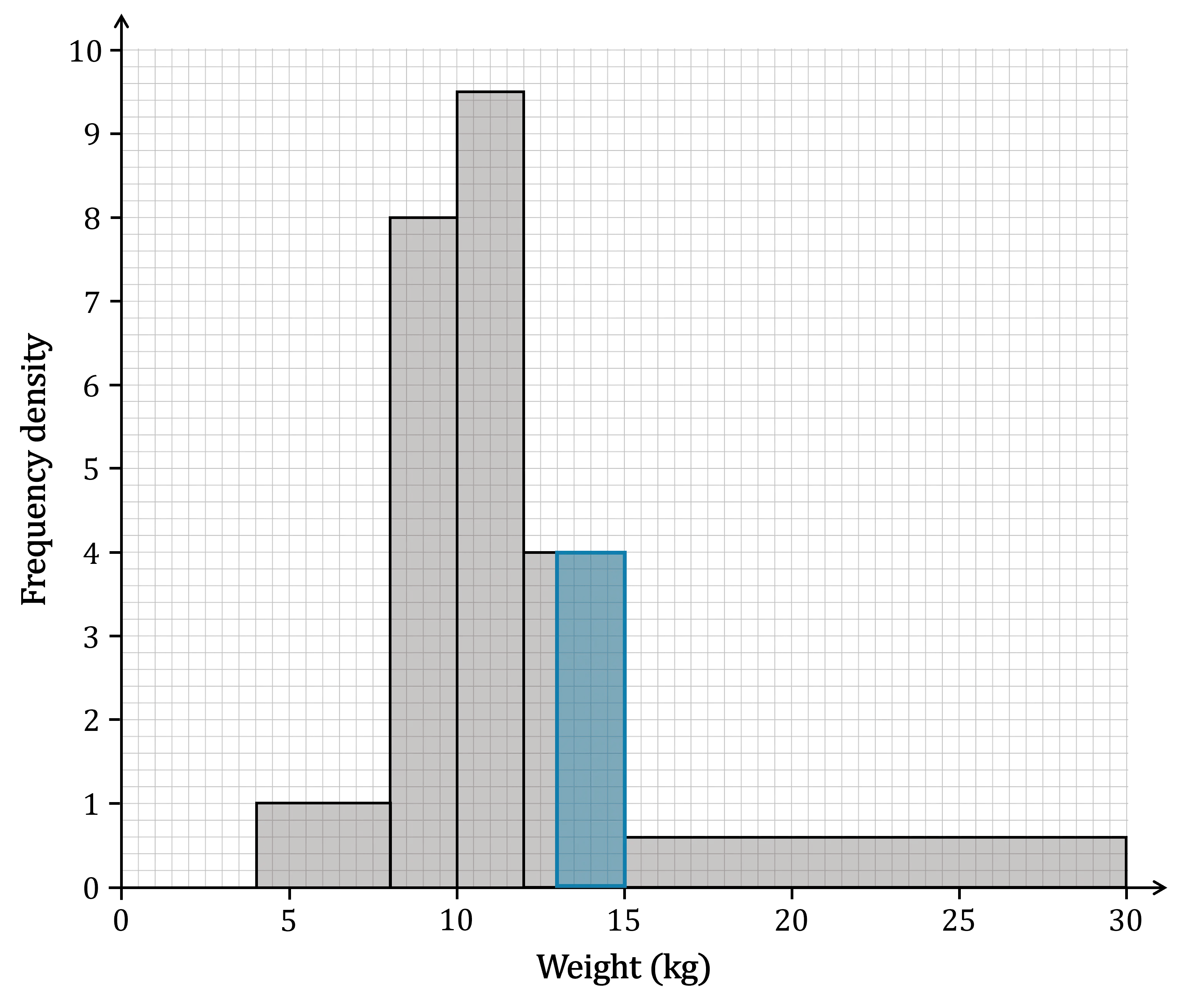
The histogram from the question with the bar between 13 and 15 highlighted.

Now use $frequency = frequency density \times class width$ to estimate the number of dolphins in the 13 ≤ w < 15 interval
(Note that using the histogram in this way is actually a form of linear interpolation)

$frequency = 4 \times 2 = 8$

This is only an estimate because we don't actually know that dolphins are evenly distributed across the entire 12 ≤ w < 15 class interval

Now the total number of dolphins with a weight greater than 13 kg can be estimated

$8 + 9 = 17$

There are approximately 17 dolphins with a weight greater than 13 kg

Last updated: 18 October 2024

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves: