Revision NotesExam QuestionsFlashcardsPast Papers
IGCSEMathsCambridge (CIE)ExtendedRevision NotesPythagoras & TrigonometryTrigonometric Graphs & EquationsTrigonometric Graphs

Trigonometric Graphs (Cambridge (CIE) IGCSE Maths)

Revision Note

Naomi C

Written by: Naomi C

Reviewed by: Dan Finlay

Cambridge (CIE) Maths: ExtendedEdexcel Maths A (Modular): Higher Unit 1Cambridge (CIE) International Maths: ExtendedEdexcel Maths A: Higher

Did this video help you?

Drawing Trig Graphs

What are trig graphs?

  • Trigonometric (trig) graphs are the graphs of

    • y equals sin space x

    • y equals cos space x

    • y equals tan space x

  • The variable x is like an angle

    • but the angle can now go beyond acute to become obtuse and reflex

      • 0 degree less or equal than x less or equal than 360 degree

  • Trig graphs have repeating (periodic) shapes and symmetries that you need to know

How do I draw the graph of y = sin x?

  • The graph of y equals sin space x is a wave that oscillates between heights of 1 and -1 and repeats every 360° (its period is 360°)

    • It goes through the origin, (0, 0)

    • Then every 90° it cycles through the heights 1, 0, -1, 0, ...

Graph of y=sin(x) from x = -360º to x = 360º.

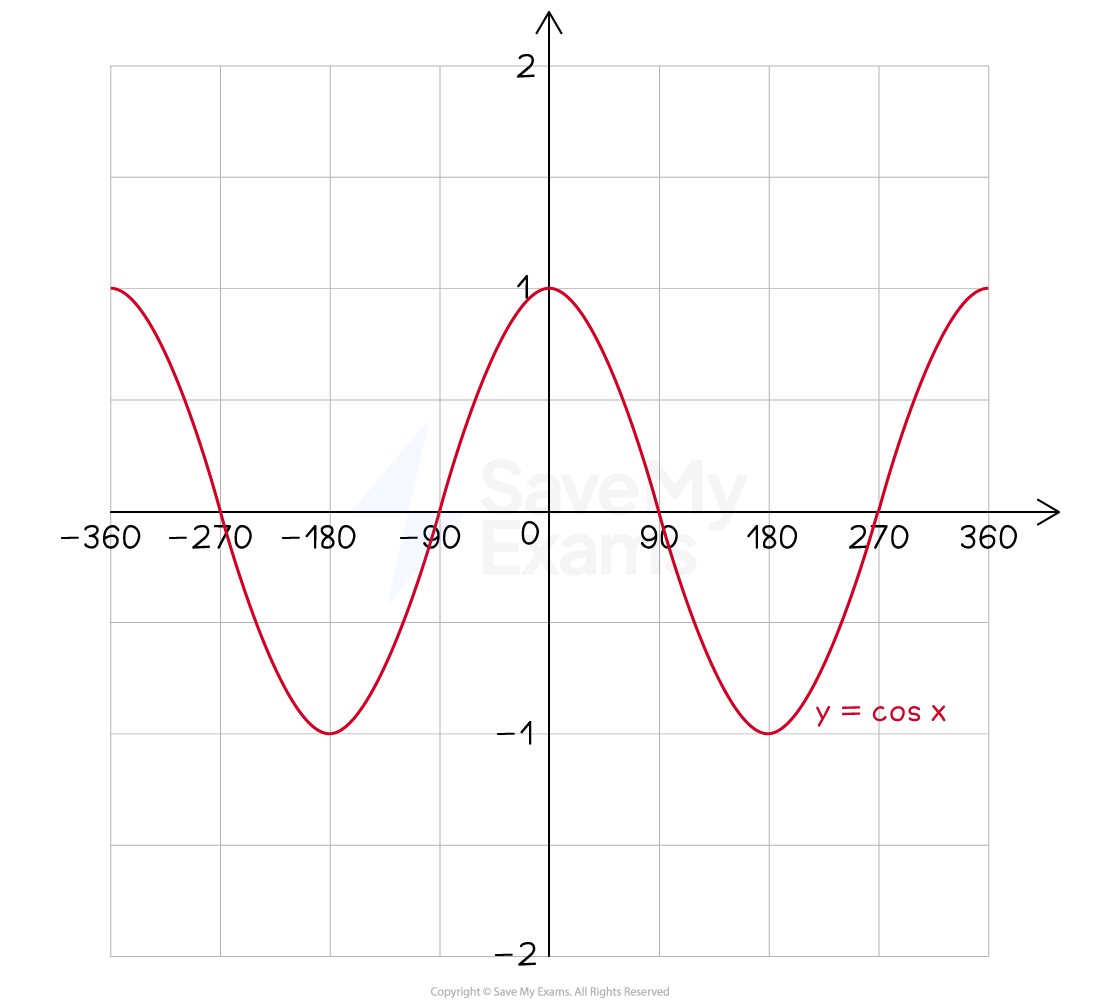
How do I draw the graph of y = cos x?

  • The graph of y equals cos space x is a wave that oscillates between heights of 1 and -1 and repeats every 360° (its period is 360°)

    • It has a y-intercept of 1, coordinates (0, 1)

    • Then every 90° it cycles through the heights 0, -1, 0, 1, ...

  • y equals cos space x is the same as translating y equals sin space x by 90 to the left

Graph of y=cos(x) from x = -360º to x = 360º.

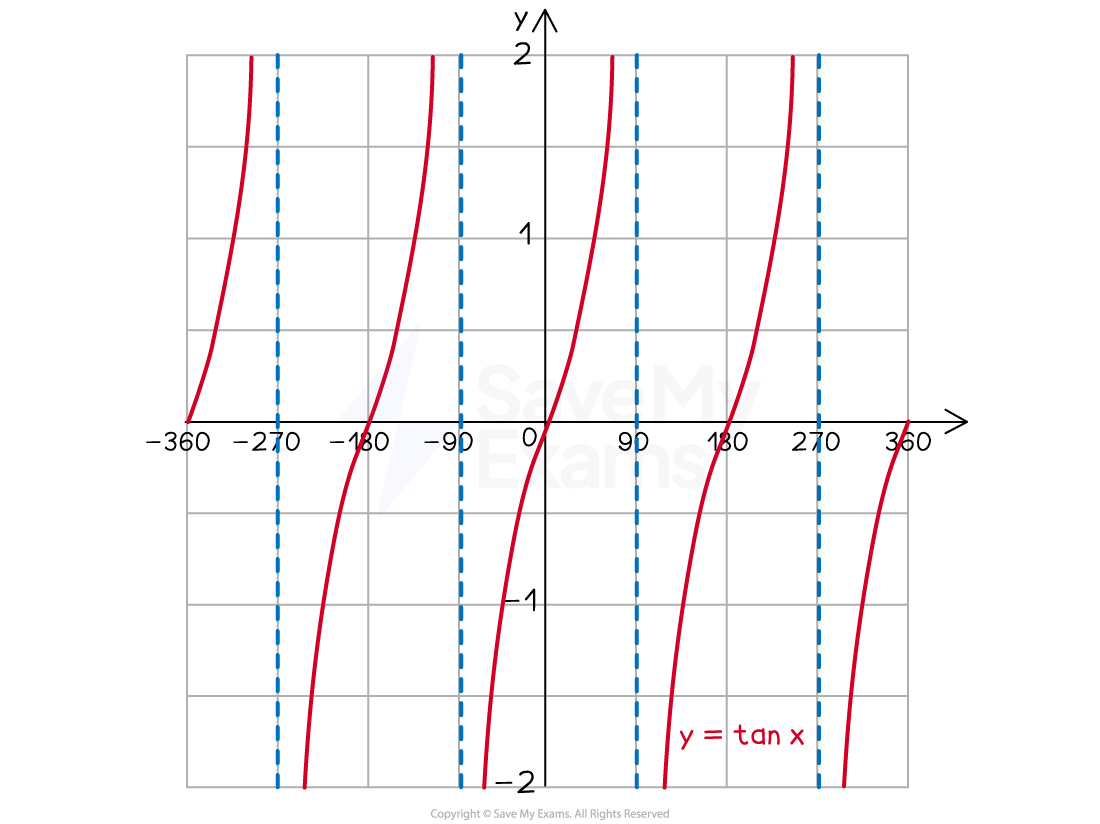
How do I draw the graph of y = tan x?

  • The graph of y equals tan space x is not a wave but consists of branches that repeat every 180° (its period is 180°)

    • This is half the period of sin space x and cos space x

  • There are dotted vertical lines that separate the branches called asymptotes

    • These are every 180° at x equals 90 degree, x equals 270 degree, ...

    • The curve cannot touch these, but get closer and closer to them

    • A branch starts down at a height of negative infinity and goes up to a height of plus infinity

  • y equals tan space x goes through the origin, (0, 0)

Graph of y=tan(x) from x = -360º to x = 360º.

Worked Example

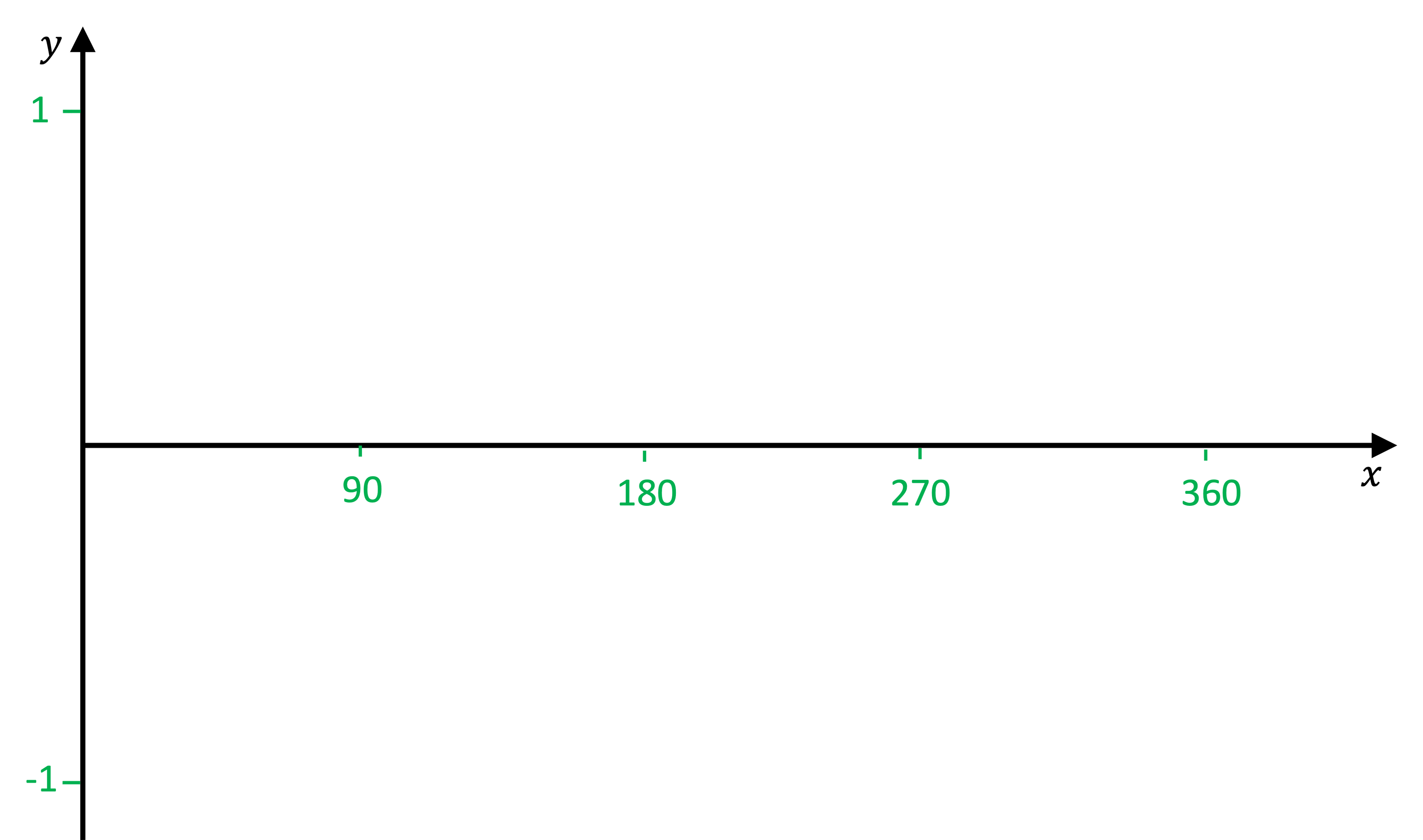
On the axes provided, sketch the graph of y equals sin space x degree for 0 less or equal than x less or equal than 360.

Mark 1 and −1 on the y-axis
Mark 0, 90, 180, 270 and 360 on the x-axis (try to space them evenly apart)

Graph with x-axis going from 0 to 360 and y-axis going from -1 to +1.

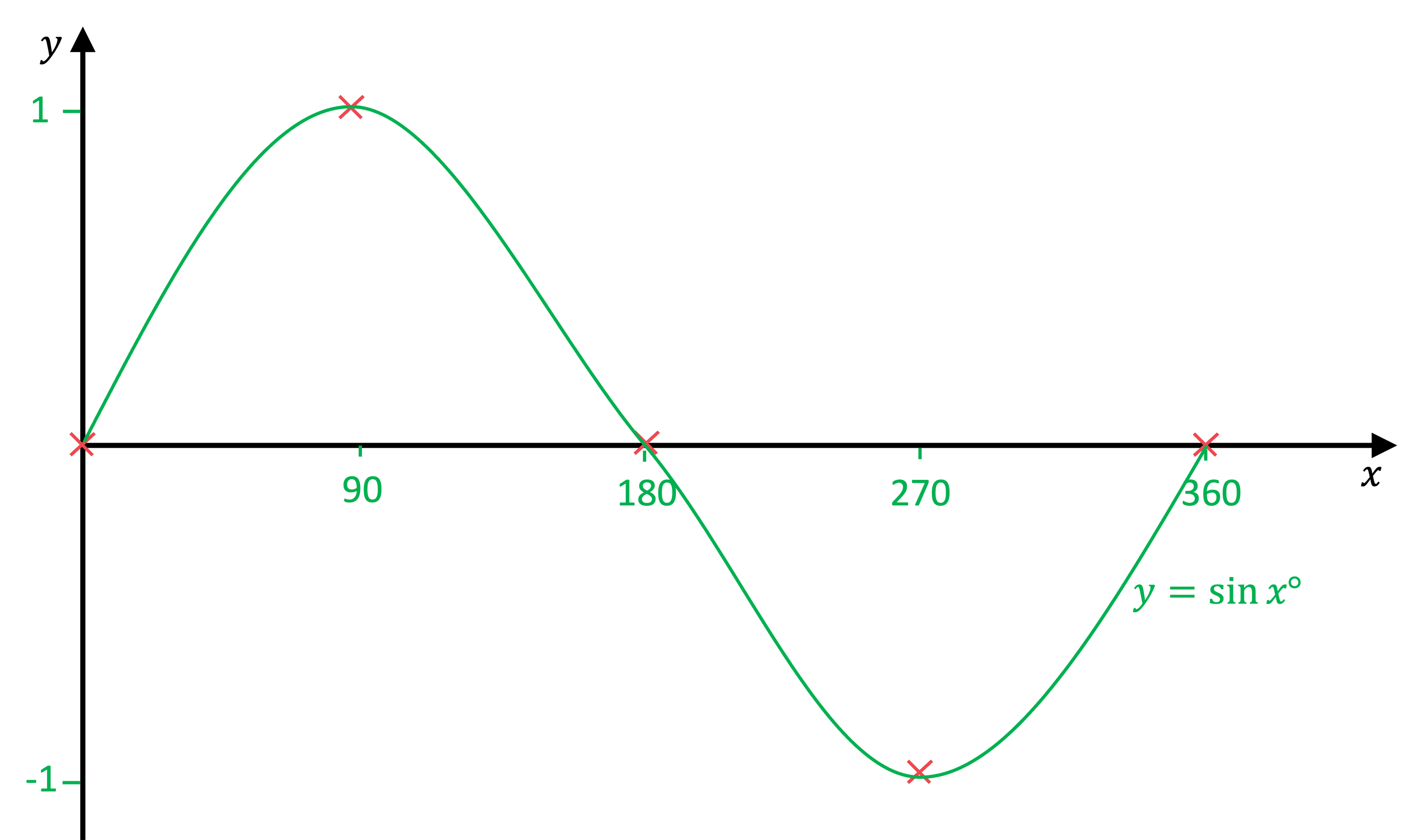
y equals sin space x starts at (0, 0) then every 90° it cycles though heights of 1, 0 , −1, 0, ...
Mark these points on the axes
Join the points with a smooth line
Label the curve with its equation

Graph of y=sin(x) from 0º to 360º.

Last updated:

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:3D Pythagoras & TrigonometryNext:Solving Trig Equations
    Author
    Reviewer
    Naomi C

    Author: Naomi C

    Expertise: Maths

    Naomi graduated from Durham University in 2007 with a Masters degree in Civil Engineering. She has taught Mathematics in the UK, Malaysia and Switzerland covering GCSE, IGCSE, A-Level and IB. She particularly enjoys applying Mathematics to real life and endeavours to bring creativity to the content she creates.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.