Congruence (Cambridge (CIE) IGCSE Maths)
Revision Note
Written by: Naomi C
Reviewed by: Dan Finlay
Congruence
What is congruence?
Two shapes are congruent if they are identical in shape and size
One may be a reflection, rotation, or translation of the other
If one shape is an enlargement of the other, then they are not identical in size and so are not congruent
How do we prove that two shapes are congruent?
To show that two shapes are congruent you need to show that they are both the same shape and the same size
If a shape has been reflected, rotated or translated, then its image is congruent to it
Show that corresponding sides are the same length
Show that corresponding angles are the same size
You do not need to show that they are facing in the same direction
Examiner Tips and Tricks
Tracing paper can help in the exam if you are unsure whether two shapes are congruent
Trace over one shape and then see if it fits exactly on top of the other
Only do this if the image is drawn to scale
Worked Example
Write down the letters of the two shapes below which are congruent to A.
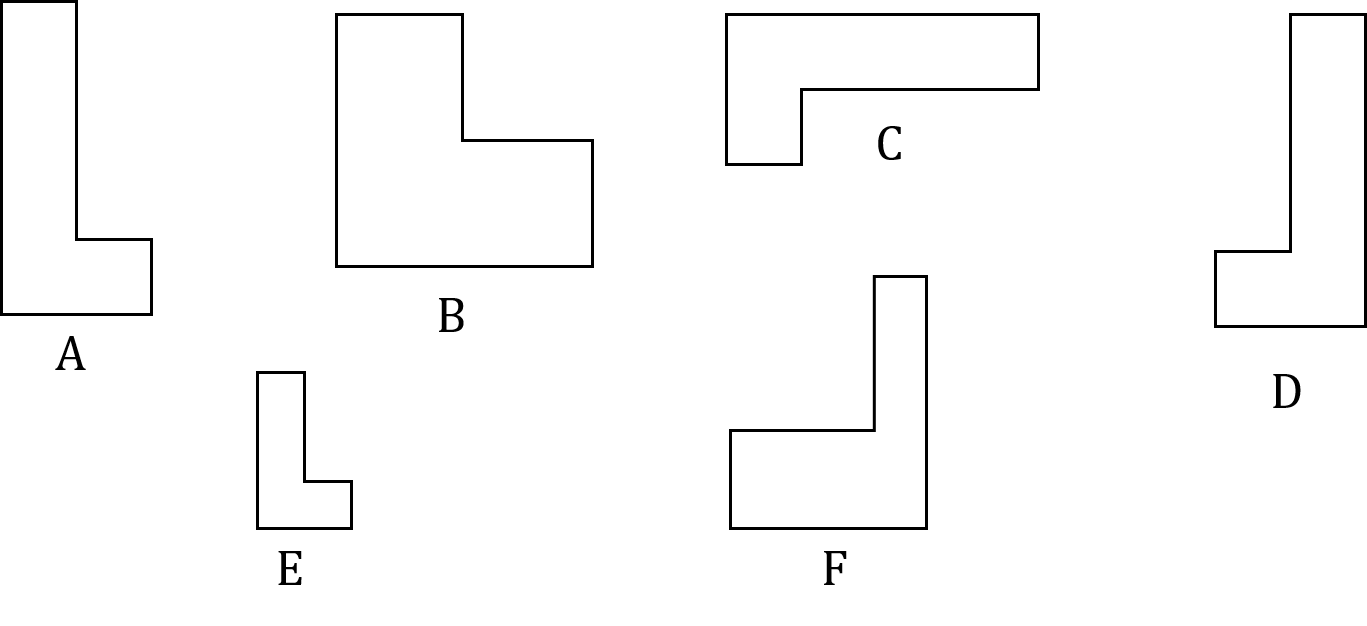
Shapes C and D are congruent to A
Last updated:
You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
