Revision NotesExam QuestionsFlashcardsPast Papers
IGCSEMathsCambridge (CIE)ExtendedRevision NotesCoordinate Geometry & GraphsDifferentiationProblem Solving with Differentiation

Problem Solving with Differentiation (Cambridge (CIE) IGCSE Maths)

Revision Note

Mark Curtis

Written by: Mark Curtis

Reviewed by: Dan Finlay

Cambridge (CIE) Maths: ExtendedEdexcel Maths A (Modular): Higher Unit 2Edexcel Maths A: Higher

Did this video help you?

Problem Solving with Differentiation

What is problem solving using differentiation?

  • You can use the same method of differentiating curves to find turning points to help with problems involving finding the maximum or minimum value of a quantity

    • These are called optimisation problems

  • Questions may use different variables

    • For example, A equals t cubed minus 12 t and fraction numerator straight d A over denominator straight d t end fraction equals 0

How do I apply differentiation to different contexts?

  • This is easiest explained using an example

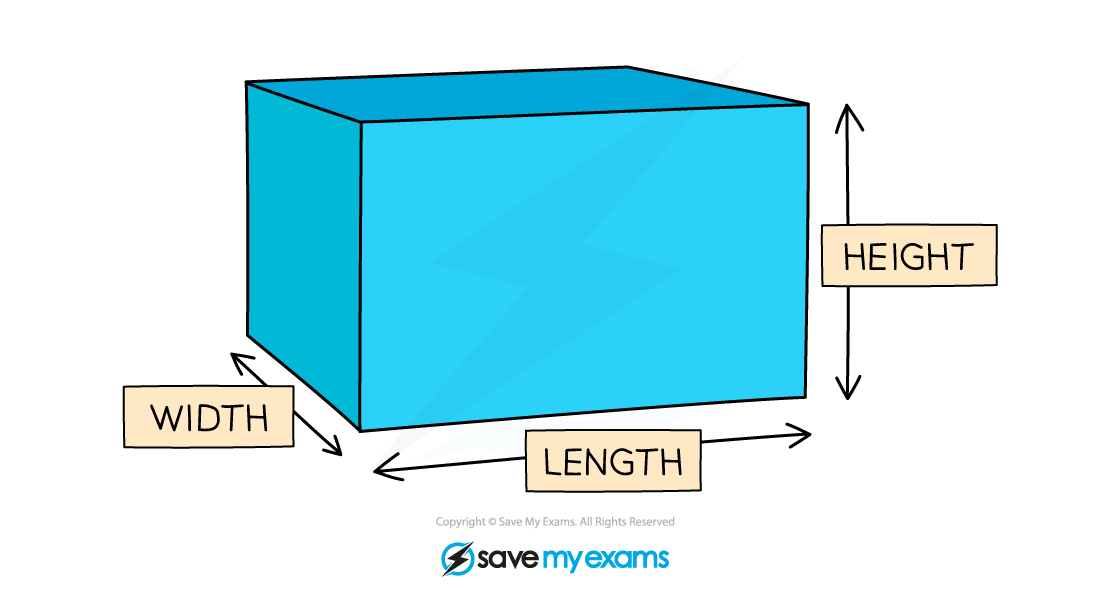
Diagram of a cuboid with the width, length and height labelled.

  • Find the maximum volume, V m3, of the cuboid shown with width 2 m, length x m and height open parentheses 10 minus x close parentheses m

    • Find a formula for its volume in terms of x

    • Volume = width cross times length cross times height

      • V equals 2 x open parentheses 10 minus x close parentheses

    • Expand this into individual terms in x

      • V equals 20 x minus 2 x squared

      • This is a negative quadratic in x (it has an intersection shape)

  • The graph of V against x will have a maximum point when fraction numerator straight d V over denominator straight d x end fraction equals 0

    • Find fraction numerator straight d V over denominator straight d x end fraction by differentiating each term

      • fraction numerator straight d V over denominator straight d x end fraction equals 20 minus 4 x

    • Set this equal to zero and solve

      • table row cell 20 minus 4 x end cell equals 0 end table so 4 x equals 20 giving x equals 5

      • This is the value of x at the maximum point (not the value of V)

    • Substitute this value of x back into the equation for V

      • V equals 20 cross times 5 minus 2 cross times 5 squared equals 50

      • The maximum volume is 50 m3

Examiner Tips and Tricks

A common problem in the exam is to forget to substitute the value of x back into the formula!

How do I know if I have found a maximum value or a minimum value?

  • Sometimes there are two values of x for different turning points and you need one of them

    • either substitute them both back into the formula

      • See which gives the max value and which gives the min value

    • or use any acceptable techniques for classifying turning points

      • For example, using a sketch to see if its a max or min

    • Remember that

      • Positive quadratics have minimum points

      • Negative quadratics have maximum points

How do I use differentiation if there are lots of variables?

  • Sometimes a formula has lots of letters

    • You need to find an extra relationship between these letters

    • then substitute it into the formula

  • If, in the above example, you had width 2 m, length x m and height y m then

    • V equals 2 x y

      • But you need a formula in x only

    • You will be given an extra piece of information, such as the length and height sum to 10 m

      • Therefore x plus y equals 10

      • Make y the subject, y equals 10 minus x

      • Substitute it into V to get V equals 2 x open parentheses 10 minus x close parentheses

Worked Example

A farmer has 60 metres of fencing and wants to fence off the biggest rectangular area possible next to an existing wall.

The area has dimensions x metres by y metres, as shown.

Image of the farmer's fence attached to a wall. There are three sides of fencing forming a rectangular area with the wall. The width of the rectangle is x and the length is y.

(a) Explain why 2 x plus y equals 60.

The wall is not part of the fencing

Find the total length of the three sides of the fence shown

x plus y plus x

This must equal 60 metres

The length of the fence must equal 60 metres so bold 2 bold italic x bold plus bold italic y bold equals bold 60

(b) Show that the area, Am2, is given by A equals 60 x minus 2 x squared.

Find the area of the rectangle shown

A equals x y

You need a right-hand side in terms of x only

Make y the subject of part (a)

y equals 60 minus 2 x

Substitute this into the area formula

A equals x open parentheses 60 minus 2 x close parentheses

This is now all in terms of x

Expand

bold italic A bold equals bold 60 bold italic x bold minus bold 2 bold italic x to the power of bold 2

(c) Find the maximum possible area.

To find a maximum point, set fraction numerator straight d A over denominator straight d x end fraction equals 0

First find fraction numerator straight d A over denominator straight d x end fraction by differentiating each term

fraction numerator straight d A over denominator straight d x end fraction equals 60 minus 4 x

Set this equal to zero and solve

table row cell 60 minus 4 x end cell equals 0 row cell 4 x end cell equals 60 row x equals cell 60 over 4 end cell row x equals 15 end table

This is the value of x at the maximum point (but not the maximum of A)

Substitute this value of x back into A

table row A equals cell 60 cross times 15 minus 2 cross times 15 squared end cell row blank equals 450 end table

The maximum area is 450 m2

(d) Explain how you know that the answer in part (c) is a maximum area, not a minimum area.

See how the area A depends on x

Think about what it would look like as a graph

A equals 60 x minus 2 x squared is a negative quadratic curve

A negative quadratic curve has an intersection shape

There is only one turning point on this graph and it is a maximum point

The curve bold italic A bold equals bold 60 bold italic x bold minus bold 2 bold italic x to the power of bold 2 is a negative quadratic curve

This means it can only have a maximum point, not a minimum point

Last updated:

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:Classifying Stationary PointsNext:Rotational Symmetry
    Author
    Reviewer
    Mark Curtis

    Author: Mark Curtis

    Expertise: Maths

    Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.