Classifying Stationary Points (Cambridge (CIE) IGCSE Maths)

Revision Note

Test yourself Flashcards

Written by: Jamie Wood

Reviewed by: Dan Finlay

Did this video help you?

Classifying Stationary Points

What are the different types of stationary points?

You need to know two different types of stationary points:
- Maximum points (this is where the graph reaches a “peak”)
- Minimum points (this is where the graph reaches a “trough”)
  - These are also called turning points
  - Deciding which is which is called classifying them (or finding the nature of them)

Two graphs, the first has a maximum point labelled and the second has a minimum point labelled.

If a graph has multiple turning points, the one you are interested in can be described as a local maximum or minimum point
- Other parts of the graph may still reach higher/lower values elsewhere

How do I classify turning points using graphs?

You can use the shape of common graphs to classify different turning points
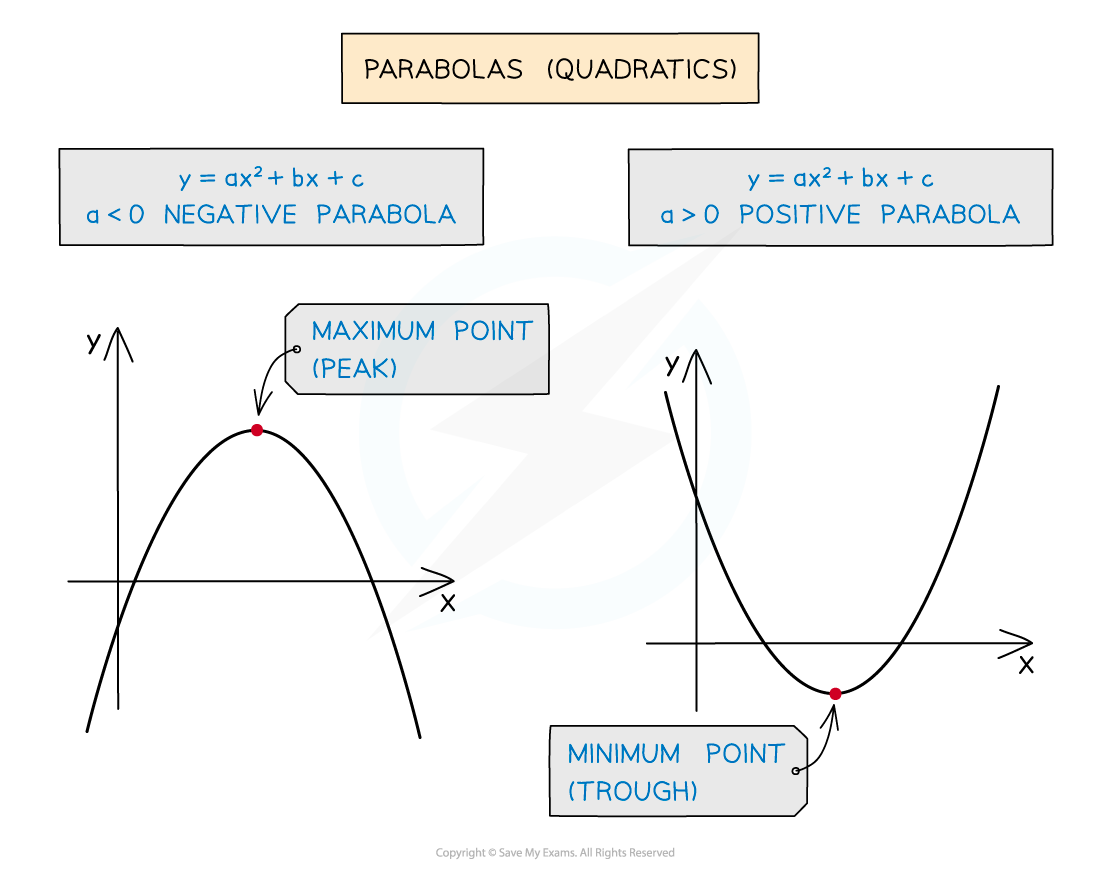
To classify the turning point on a quadratic curve (parabola), remember that:
- A positive quadratic (positive x² term) must have a minimum point
- A negative quadratic (negative x² term) must have a maximum point

Two graphs. The first graph is a negative quadratic where a<0, and has the maximum point labelled. The second graph is a positive quadratic where a>0, and has the minimum point labelled.

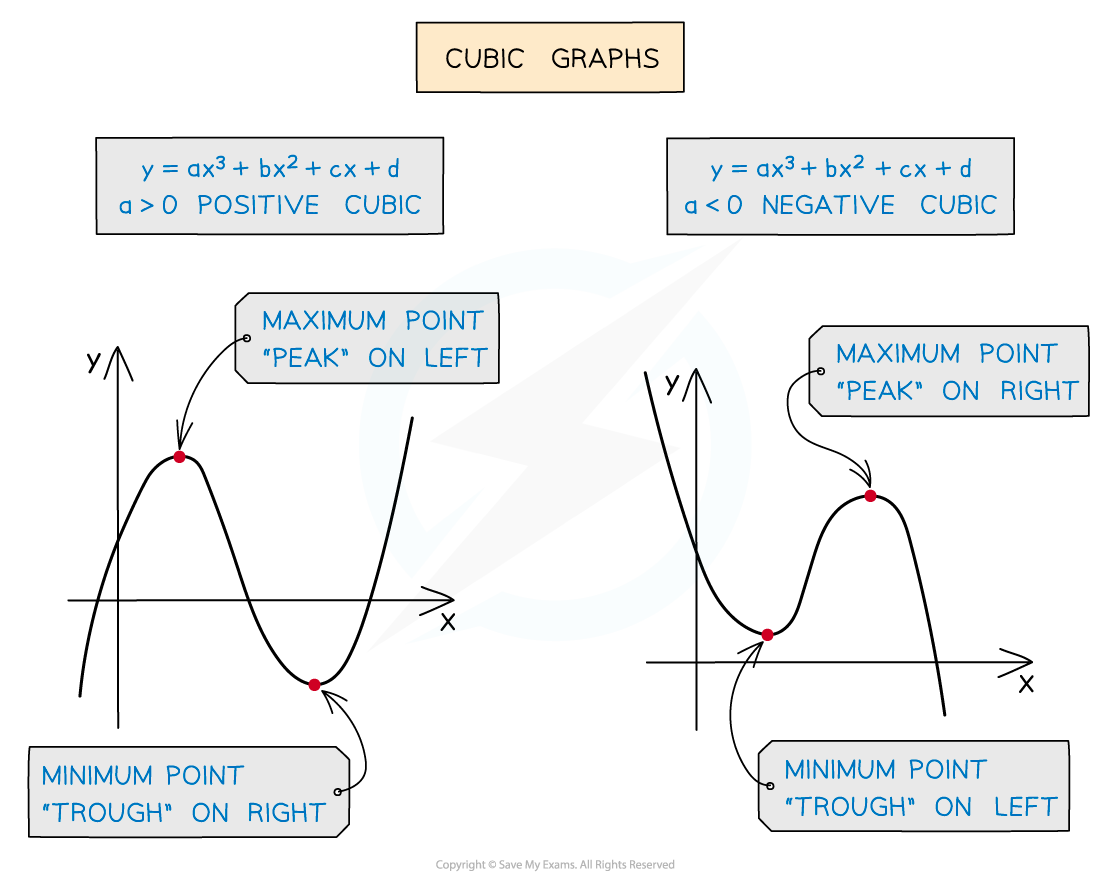
To classify two different turning points on a cubic curve, remember that:
- A positive cubic has a maximum point on the left and a minimum on the right
- A negative cubic has a minimum point on the left and a maximum on the right

Turn Pts Notes fig6, downloadable IGCSE & GCSE Maths revision notes

How do I classify turning points using the gradient function (derivative)?

An alternative method if no graph is available is to use the gradient function (derivative) $\frac{d y}{d x}$
- By looking at the gradient just before and just after a turning point, you can determine if it is a maximum or a minimum
- Find the gradient just before and just after a turning point by substituting values near to the value of x into the gradient function
- It helps to imagine what the tangents to the curve would look like

Gradient before turning point	Gradient at turning point	Gradient after turning point	Type of turning point
Positive /	Zero ⁻	Negative \	Maximum /^—\
Negative \	Zero _	Positive /	Minimum \_/

Gradient before turning point

Gradient at turning point

Gradient after turning point

Type of turning point

Positive

Zero

⁻

Negative

Maximum

/^—\

Negative

Zero

Positive

Minimum

\_/

How do I classify turning points using the second derivative?

Another method is to use the second derivative, $\frac{d^{2} y}{d x^{2}}$ , which is the derivative-of-the-derivative
- $\frac{d^{2} y}{d x^{2}}$ is pronounced "d-two-y by dx-squared"
Differentiate the equation once to get $\frac{d y}{d x}$ then again to get $\frac{d^{2} y}{d x^{2}}$
- This is the same as differentiating the original equation for $y$ twice
If the stationary point is at $x = a$ , substitute $x = a$ into the expression for $\frac{d^{2} y}{d x^{2}}$ to get a numerical value
- If the result is negative, $\frac{d^{2} y}{d x^{2}} < 0$ , then the stationary point is a maximum point
  - This is often the opposite of what people expect!
- If the result is positive, $\frac{d^{2} y}{d x^{2}} > 0$ , then the stationary point is a minimum point
- If the value is zero, $\frac{d^{2} y}{d x^{2}} = 0$ , then the test has failed
  - You will need to try another method to classify the turning point

Worked Example

The turning points on the curve with equation $y = 2 x^{3} + 3 x^{2} - 12 x + 1$ are (-2, 21) and (1, -6).

Determine the nature of these turning points.

Method 1: Using the graph

Make a quick sketch of the curve
It is a positive cubic so you know that it will start at the bottom left, have two turning points and go towards the top right
You know the coordinates of the turning points and the y-intercept: (0, 1)
(the sketch does not have to be perfect!)

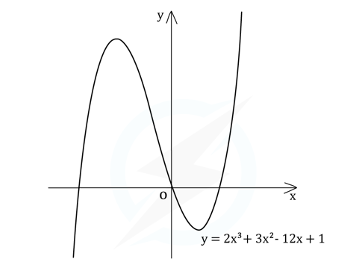
Graph of the curve with equation y=2x³+2x²-12x+1.

From the graph, which is a positive cubic,
(-2, 21) is to the left of (1, -6)

Therefore, (-2, 21) is a maximum point and (1, -6) is a minimum point

Method 2: Differentiation (1^st derivative)

Differentiate the original equation to find the 1^st derivative, the gradient function, $\frac{d y}{d x}$

$\begin{matrix} 2 x^{3} & \to & 6 x^{2} \\ 3 x^{2} & \to & 6 x \\ - 12 x & \to & - 12 \\ 1 & \to & 0 \end{matrix}$

$\frac{d y}{d x} = 6 x^{2} + 6 x - 12$

Find the gradient just before and just after each turning point by substituting a suitable x-value into the gradient function

Turning point

Gradient before

Gradient after

(-2, 21)

sub x = -3

6(-3)² + 6(-3) - 12 = 24

sub x = -1

6(-1)² + 6(-1) - 12 = -12

(1, -6)

sub x = 0

6(0)² + 6(0) - 12 = -12

sub x = 2

6(2)² + 6(2) - 12 = 24

The gradient just before (-2, 21) is positive and the gradient just after is negative, therefore the turning point here is a maximum point

The gradient just before (1, -6) is negative and the gradient just after is positive, therefore the turning point here is a minimum point

Method 3: Differentiation (2^nd derivative)

Differentiate the original equation to find the 1^st derivative

$\begin{matrix} 2 x^{3} & \to & 6 x^{2} \\ 3 x^{2} & \to & 6 x \\ - 12 x & \to & - 12 \\ 1 & \to & 0 \end{matrix}$

$\frac{d y}{d x} = 6 x^{2} + 6 x - 12$

Differentiate again to find the 2^nd derivative

$\begin{matrix} 6 x^{2} & \to & 12 x \\ 6 x & \to & 6 \\ - 12 & \to & 0 \end{matrix}$

$\frac{d y}{d x} = 12 x + 6$

Find the nature of each turning point by substituting the value of its x-coordinate into the 2^nd derivative
A negative result indicates a maximum point (or positive for a minimum point)

For (-2, 21): $\frac{d y}{d x} = 12 (- 2) + 6 = - 18$

The second derivative is negative, therefore the turning point at (-2, 21) is a maximum point

For (1, -6): $\frac{d y}{d x} = 12 (1) + 6 = 18$

The second derivative is positive, therefore the turning point at (1, -6) is a minimum point

Last updated: 17 October 2024

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves: