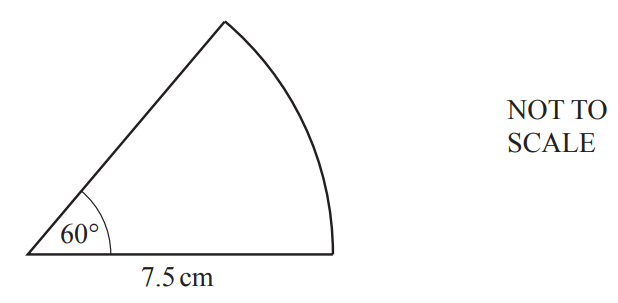
Calculate the area of this sector of a circle.
.......................................... cm2
Did this page help you?
Exam code: 0580 & 0980
Select a download format for Circles, Arcs & Sectors
Select an answer set to view for
Circles, Arcs & Sectors

Calculate the area of this sector of a circle.
.......................................... cm2
How did you do?
Did this page help you?

The diagram shows a sector of a circle with radius 6.2 cm and sector angle 217°.
Calculate the area of this sector.
............................................. cm2
How did you do?
Did this page help you?
Calculate the area of a circle with radius 5.1 cm.
......................................cm2
How did you do?
Did this page help you?
The diagram shows a sector of a circle of radius 4 cm.

Work out the length of the arc .
Give your answer correct to 3 significant figures.
How did you do?
Did this page help you?
The diagram shows sector of a circle, centre

Angle
Calculate the area of sector
Give your answer correct to one decimal place.
How did you do?
Did this page help you?

The diagram shows a sector of a circle with centre , radius 8 cm and sector angle 165°.
Calculate the total perimeter of the sector.
............................................ cm
How did you do?
Did this page help you?

The diagram shows the surface of a garden pond, made from a rectangle and two semicircles.
The rectangle measures 3 m by 1.2 m.
Calculate the area of this surface.
...............................................m2
How did you do?
Did this page help you?

The cross-section of a gate is a sector of a circle with radius 8.5 m and angle 76°.
Calculate the perimeter of the sector.
............................................ m
How did you do?

A solid metal cone has radius 10 cm and height 36 cm.
i) Calculate the volume of this cone. [The volume, , of a cone with radius
and height
is
.]
......................................... cm3[2]
ii) The cone is cut, parallel to its base, to give a smaller cone.

The volume of the smaller cone is half the volume of the original cone.
The smaller cone is melted down to make two different spheres.
The ratio of the radii of these two spheres is 1 : 2.
Calculate the radius of the smaller sphere.
[The volume, , of a sphere with radius
is
.]
.......................................... cm [4]
How did you do?
Did this page help you?
The diagram shows the top of Levi's birthday cake.

The top of the cake is in the shape of a circle.
The diameter of the circle is 7 inches.
A ribbon is going to be put around the side of the cake. Ribbons are sold in 50 cm lengths.
1 inch is 2.54 cm.
Work out if one length of ribbon is long enough to go all the way around the cake.
You must show your working.
How did you do?
Did this page help you?
is a sector of a circle with centre
and radius 7 cm.

The area of the sector is 40 cm2.
Calculate the perimeter of the sector.
Give your answer correct to 3 significant figures.
How did you do?
Did this page help you?
The diagram shows a circle with centre

and
are points on the circle so that the length of the arc
is 5 cm.
Given that angle = 55°
work out the area of the circle.
Give your answer correct to one decimal place.
How did you do?
Did this page help you?
The diagram shows Yuen’s garden.

The garden is in the shape of a semicircle of radius . Yuen is going to cover his garden with grass seed.
Yuen has 12 boxes of grass seed.
Each box of grass seed contains enough seed to cover of the garden.
Has Yuen enough grass seed for his garden?
Show your working clearly.
How did you do?
Did this page help you?
Calculate the area of the sector of a circle with radius 65 mm and sector angle 42°.
Give your answer in square centimetres.
................................................ cm2
How did you do?
Did this page help you?

The arc is a quarter of a circle with centre
and radius 4.8 cm.
is a chord of the circle.
Work out the area of the shaded segment.
Give your answer correct to 3 significant figures.
How did you do?
Did this page help you?

is a sector of a circle, centre
.
is a sector of a circle, centre
.
and
are straight lines.
Angle
Calculate the perimeter of the shaded region.
Give your answer correct to 3 significant figures.
How did you do?
Did this page help you?

is a sector of a circle with centre
and radius 11 cm.
is the point on
and
is the point on
such that
is an equilateral triangle of side 7 cm.
Calculate the area of the shaded region as a percentage of the area of the sector .
Give your answer correct to 1 decimal place.
How did you do?
Did this page help you?
The diagram shows a shaded shape made from a semicircle
and a right-angled triangle
.

is the diameter of the semicircle
.
Work out the perimeter of the shaded shape.
Give your answer correct to 3 significant figures.
....................
How did you do?
Did this page help you?

The diagram shows a square with side length 8 cm and a sector of a circle with radius 9.5 cm and sector angle °. The perimeter of the square is equal to the perimeter of the sector.
Calculate the value of .
................................................
How did you do?
Did this page help you?

In the diagram, A, B, C and D lie on the circle, centre O.
Angle ADC = 128°, angle ACD = 28° and angle BCO = 30°. Angle AOC = 104°.
The radius, OC, of the circle is 9.6 cm.
Calculate the total perimeter of the sector OADC.
.............................................. cm
How did you do?
Did this page help you?

The diagram shows a sector of a circle of radius . The arc length is
.
i) Calculate the value of .
= .............................................. [2]
ii) Calculate the area of the sector.
........................................ cm2 [2]
How did you do?
Did this page help you?

P, Q and R are points on the circumference of the circle, centre O.
PO is parallel to QR and angle POQ = 48°.
Find angle OPR.
Angle OPR = ...............................................
How did you do?
The radius of the circle is 5.4 cm.
Calculate the length of the major arc PQ.
.......................................... cm
How did you do?
Did this page help you?
The diagram shows a plan of Brian's lawn.

The edge of the lawn consists of two semicircles and two straight lines.
Each semicircle has centre .
The diameters of the semicircles are 9 m and 5 m.
Brian is going to put lawn edging around the edge of the lawn.
Lawn edging is sold in 2.4 metre rolls.
Brian has £35
Lawn edging £3.99 per roll or 3 rolls for £10 |
Has Brian got enough money to buy all the rolls of lawn edging he needs?
You must show all your working.
How did you do?
Did this page help you?
Saphia is organising a conference.
People at the conference will sit at circular tables.

Each table has a diameter of 140 cm.
Each person needs 60 cm around the circumference of the table.
There are 12 of these tables in the conference room.
A total of 90 people will be at the conference.
Are there enough tables in the conference room?
How did you do?
Did this page help you?

and
are points on a circle of radius 5 cm, centre
.
and
are tangents to the circle.
Work out the length of arc .
Give your answer correct to 3 significant figures.
How did you do?
Did this page help you?

The diagram shows a sector of a circle of radius 8 cm. The length of the arc is 6.4 cm.
Find the area of the sector.
.......................................... cm2
How did you do?
Did this page help you?
The total perimeter of a semicircle is 19.02 cm.
Calculate the radius of the semicircle.
................................................ cm
How did you do?
Did this page help you?

and
lie on a circle, centre
.
Calculate the length of the arc .
How did you do?
Did this page help you?

The diagram shows a company logo made from a rectangle and a major sector of a circle.
The circle has centre O and radius OA.
OA = OD = 0.5 cm and AB = 1.5 cm.
E is a point on OC such that OE = 0.25 cm and angle OED = 90°.
Calculate the perimeter of the logo.
............................................. cm
How did you do?
Calculate the area of the logo.
............................................ cm2
How did you do?
Did this page help you?

The diagram shows a circle, centre O.
The straight line ABC is a tangent to the circle at B.
OB = 8 cm, AB = 15 cm and BC = 22.4 cm.
AO crosses the circle at X and OC crosses the circle at Y. Calculate angle XOY.
Angle XOY = ...............................................
How did you do?
Calculate the length of the arc XBY.
.......................................... cm
How did you do?
Calculate the total area of the two shaded regions.
........................................ cm2
How did you do?
Did this page help you?

The diagram shows a design made from a triangle AOC joined to a sector OCB.
AC = 8cm, OB = OC = 7 cm and angle ACO = 78°.
Use the cosine rule to show that OA = 9.47 cm, correct to 2 decimal places.
How did you do?
Calculate angle OAC.
Angle OAC = ................................................
How did you do?
The perimeter of the design is 29.5 cm.
Show that angle COB = 41.2°, correct to 1 decimal place.
How did you do?
Calculate the total area of the design.
......................................... cm2
How did you do?
Did this page help you?