Revision NotesExam QuestionsFlashcardsPast Papers
IGCSEMathsCambridge (CIE)ExtendedRevision NotesPythagoras & TrigonometryTrigonometric Graphs & EquationsSolving Trig Equations

Solving Trig Equations (Cambridge (CIE) IGCSE Maths)

Revision Note

Naomi C

Written by: Naomi C

Reviewed by: Dan Finlay

Cambridge (CIE) Maths: ExtendedEdexcel Maths A (Modular): Higher Unit 1Edexcel Maths A: HigherCambridge (CIE) International Maths: Extended

Solving Trig Equations

What are trig equations?

  • Trig equations are equations involving sin space x, cos space x and tan space x

  • They often have multiple solutions

    • A calculator gives the first solution

    • You need to use trig graphs to find the others

    • The solutions must lie in the interval (range) of x given in the question, e.g. 0 degree less or equal than x less or equal than 360 degree

How do I solve sin x = ...?

  • Find the first solution of the equation by taking the inverse sin function on your calculator (or using an exact trig value)

    • E.g. For the first solution of the equation sin space x equals 0.5 for 0 degree less or equal than x less or equal than 360 degree

      • This gives x equals sin to the power of negative 1 end exponent open parentheses 0.5 close parentheses equals 30 degree

  • Then sketch the sine graph for the given interval

    • Identify the first solution on the graph

    • Use the symmetry of the graph to find additional solutions

    • E.g. For the equation sin space x equals 0.5 for 0 degree less or equal than x less or equal than 360 degree

      • Sketch the graph y equals sin space x for 0 degree less or equal than x less or equal than 360 degree

      • Draw on sin open parentheses 30 close parentheses equals 0.5

      • By the symmetry, the new value of x is 180 degree minus 30 degree equals 150 degree

      • The solutions are 30 degree or 150 degree

Graph of y=sin(x) from x=0º to x=360º. The graph shows vertical lines at 30º and 150º that meet the curve at y=0.5.

  • Check the solutions

    • E.g. For the equation sin space x equals 0.5 for 0 degree less or equal than x less or equal than 360 degree

      • Substitute x equals 30 degree and x equals 150 degree in to the calculator

      • sin open parentheses 30 close parentheses and sin open parentheses 150 close parentheses both give a value of 0.5, so are correct

  • In general, if x is an acute solution to sin space x equals...

    • Then 180 minus x is an obtuse solution to the same equation

How do I solve cos x = ...?

  • Find the first solution of the equation by taking the inverse cos function (or using an exact trig value)

    • E.g. For the first solution of the equation cos space x equals 0.5 for 0 degree less or equal than x less or equal than 360 degree

      • This gives x equals cos to the power of negative 1 end exponent open parentheses 0.5 close parentheses equals 60 degree

  • Then sketch the cosine graph for the given interval

    • Identify the first solution on the graph

    • Use the symmetry of the graph to find additional solutions

    • E.g. For the equation cos space x equals 0.5 for 0 degree less or equal than x less or equal than 360 degree

      • Sketch the graph y equals cos space x for 0 degree less or equal than x less or equal than 360 degree

      • By the symmetry, the new value of x is 360 degree minus 60 degree equals 300 degree

      • The solutions are 60 degree or 300 degree

Graph of y=cos(x) from x=0º to x=360º. The graph shows vertical lines at 60º and 300º that meet the curve at y=0.5.

  • Check the solutions

    • E.g. For the equation cos space x equals 0.5 for 0 degree less or equal than x less or equal than 360 degree

      • Substitute x equals 60 degree and x equals 300 degree in to the calculator

      • cos open parentheses 60 close parentheses and cos open parentheses 300 close parentheses both give a value of 0.5 so are correct

  • In general, if x is a solution to cos space x equals...

    • Then 360 minus x is another solution to the same equation

How do I solve tan x = ...?

  • Find the first solution of the equation by taking the inverse tan function (or using an exact trig value)

    • E.g. For the first solution of the equation tan space x equals 1 for 0 degree less or equal than x less or equal than 360 degree

      • This gives x equals tan to the power of negative 1 end exponent open parentheses 1 close parentheses equals 45 degree

  • Then sketch the tangent graph for the given interval

    • Identify the first solution on the graph

    • Use the periodic nature of the graph to find additional solutions

    • E.g. For the equation tan space x equals 1 for 0 degree less or equal than x less or equal than 360 degree

      • Sketch the graph y equals tan space x for 0 degree less or equal than x less or equal than 360 degree

      • By the periodic nature, the new value of x is 45 degree plus 180 degree equals 225 degree

Graph of y=tan(x) from x=0º to x=360º. The graph shows vertical lines at 45º and 225º that meet the curve at y=1.

  • Check the solutions

    • E.g. For the equation tan space x equals 0.5 for 0 degree less or equal than x less or equal than 360 degree

      • Substitute x equals 45 degree and x equals 225 degree in to the calculator

      • tan open parentheses 45 close parentheses and tan open parentheses 225 close parentheses both give a value of 1 so are correct

  • In general, if x is a solution to tan space x equals...

    • Then x plus 180 is another solution to the same equation

How do I rearrange trig equations?

  • Trig equations may be given in a different form

    • Equations may require rearranging first

      • E.g. 2 space sin space x minus 1 equals 0 can be rearranged to sin space x equals 1 half

    • They can then be solved as usual

What do I do if the first solution from my calculator is negative?

  • Sometimes the first solution given by the calculator for xwill be negative

    • Continue sketching the graph to the left of the x-axis to help

    • Then find solutions that lie in the interval given in the question

Examiner Tips and Tricks

  • Know how to use the inverse functions on your calculator

    • It may involve exact trig values which do not need a calculator

  • Check your solutions by substituting them back into the original equation

Worked Example

Use the graph of y equals sin space x to solve the equation sin space x equals 0.25 for 0 degree less or equal than x less or equal than 360 degree.

Give your answers correct to 1 decimal place.

Use a calculator to find the first solution
Take the inverse sin of both sides

x equals sin to the power of negative 1 end exponent open parentheses 0.25 close parentheses equals 14.47751...

Sketch the graph of y equals sin space x

Mark on (roughly) where x equals 14.48 and y equals 0.25 would be

Draw a vertical line up to the curve
Draw another line horizontally across to the next point on the curve
Bring a line vertically back down to the x-axis

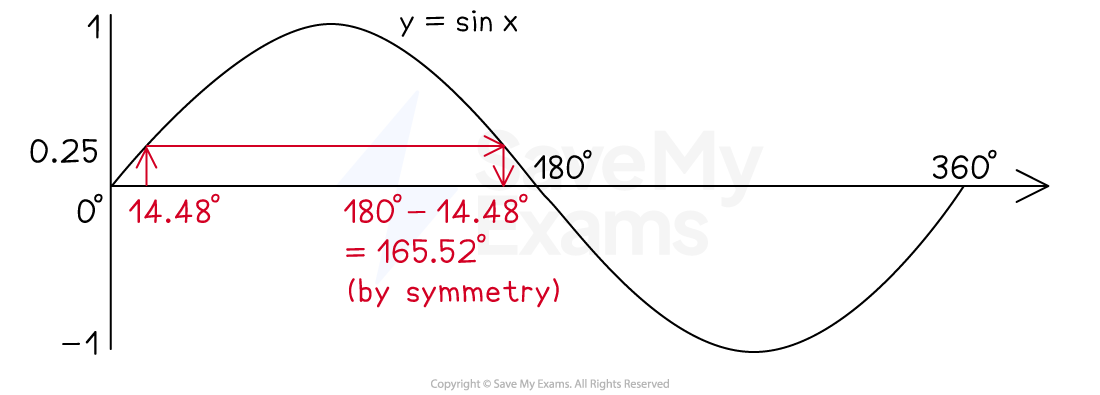
Graph of y = sin(x) from x=0º to x=360º.

Find this value using the symmetry of the curve
Subtract 14.48 from 180

180 minus 14.48 equals 165.52

Give both answers correct to 1 decimal place

bold italic x bold equals bold 14 bold. bold 5 bold degree or bold italic x bold equals bold 165 bold. bold 5 bold degree

Last updated:

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:Trigonometric GraphsNext:Introduction to Column Vectors
    Author
    Reviewer
    Naomi C

    Author: Naomi C

    Expertise: Maths

    Naomi graduated from Durham University in 2007 with a Masters degree in Civil Engineering. She has taught Mathematics in the UK, Malaysia and Switzerland covering GCSE, IGCSE, A-Level and IB. She particularly enjoys applying Mathematics to real life and endeavours to bring creativity to the content she creates.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.