Finding Stationary Points & Turning Points (Cambridge (CIE) IGCSE Maths)

Finding Stationary Points & Turning Points

What is a stationary point?

• A stationary point is a point on the graph at which the gradient is zero (a tangent drawn at this point will be horizontal)

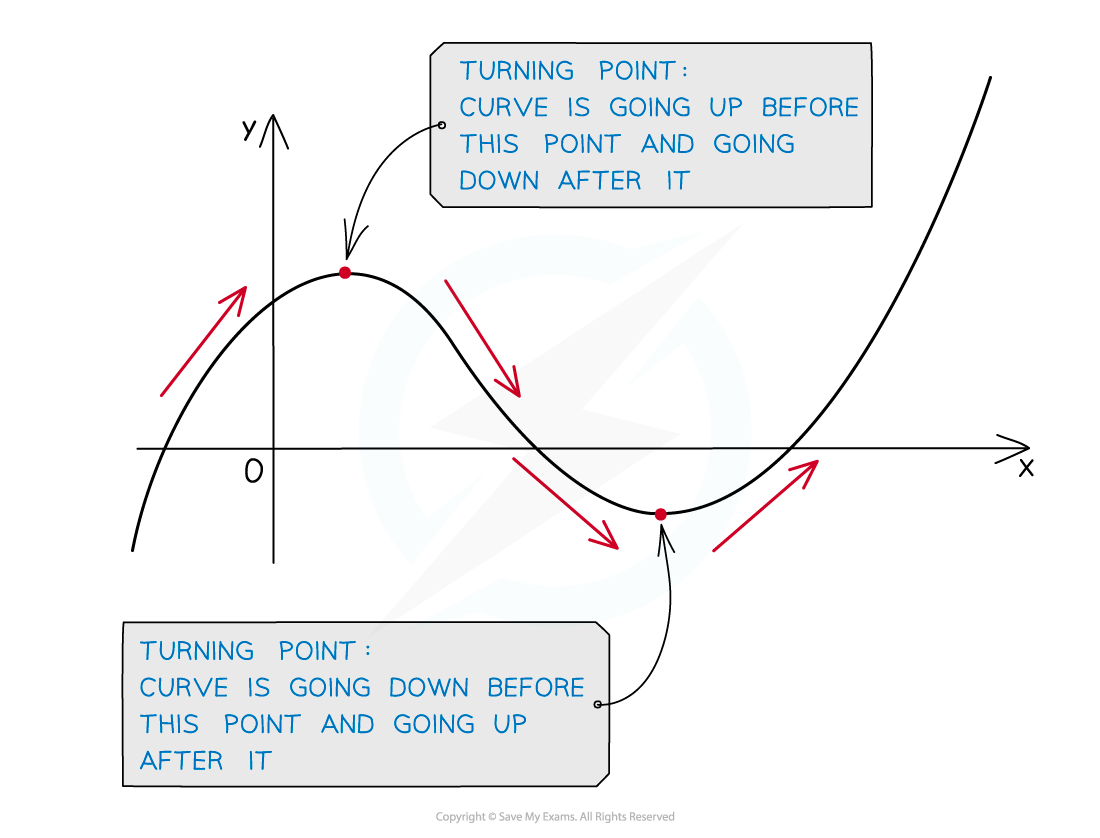
  • These include peaks (maximum points) and troughs (minimum points)

• Maximum points and minimum points are collectively know as turning points

  • At a turning point a curve changes from moving upwards to moving downwards, or vice versa

• At a turning point the gradient of the curve is zero

  • If a tangent is drawn at a turning point it will be a horizontal line

  • Horizontal lines have a gradient of zero

• Because the gradient at a turning point is zero

  • Substituting the x-coordinate of a turning point into the gradient function (the derivative) will give an output of zero 

How do I find the coordinates of a turning point?

• STEP 1
  Find the gradient function (derivative) of the original equation

  • E.g. Find the coordinates of the turning point of the equation

  • 

• STEP 2
  Set the gradient function (derivative) equal to zero and solve for

  • This will find the x-coordinate of the turning point

  • E.g. , so

• STEP 3
  Substitute the x-coordinate into the original equation of the graph

  • This will find the y-coordinate of the turning point

  • E.g.

• STEP 4

  Write out the coordinates of the turning point

  • E.g. The turning point is at