Differentiation (Cambridge (CIE) IGCSE Maths)

Revision Note

Written by: Mark Curtis

Reviewed by: Dan Finlay

Did this video help you?

Differentiation

What is a gradient function?

Recall that the equation of a curve gives the y-coordinate of a point when you substitute in its x-coordinate
- For example, $y = x^{2} + 3 x + 5$
  - Substitute $x = 2$ in to get $y = 2^{2} + 3 \times 2 + 5 = 15$
  - The point $(2, 15)$ lies on the curve
A gradient function gives the gradient of the curve at a point when you substitute in its x-coordinate
- A gradient function is written as $\frac{d y}{d x} = . . .$
  - pronounced "dy by dx"
  - This refers to the change in y over change in x
- For example, the gradient function $\frac{d y}{d x} = 2 x + 3$
  - Substitute $x = 2$ in to get $\frac{d y}{d x} = 2 \times 2 + 3 = 7$
  - The gradient at the point where $x = 2$ is 7
The gradient function $\frac{d y}{d x}$ can also be called the derivative or derived function

What is differentiation and how does it work?

Differentiation is an algebraic method that changes the equation of a curve, $y = . . .$ , into a gradient function, $\frac{d y}{d x} = . . .$
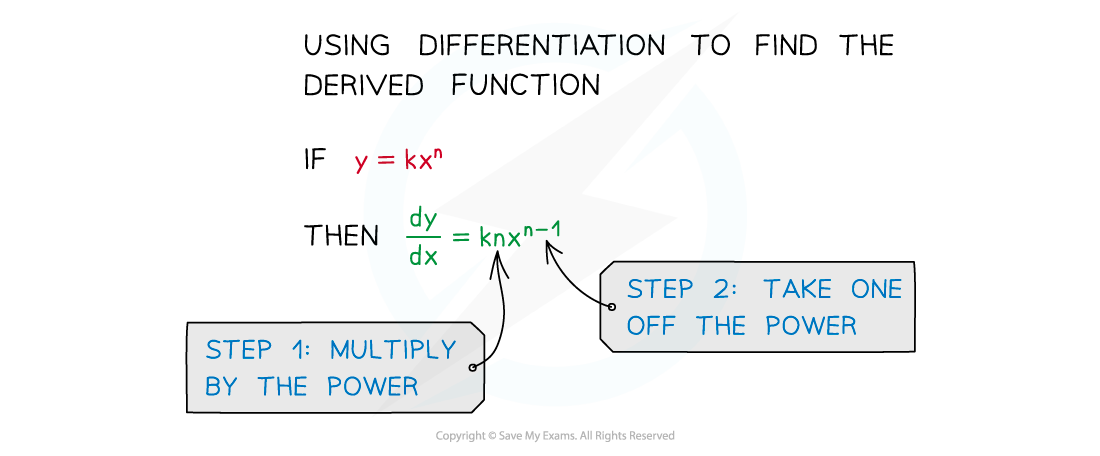
To differentiate a power of $x$ , bring down the power and reduce the power by 1
- Differentiating $y = x^{5}$ gives $\frac{d y}{d x} = 5 x^{4}$
- Differentiating $y = x^{8}$ gives $\frac{d y}{d x} = 8 x^{7}$
- Differentiating $y = x^{n}$ gives $\frac{d y}{d x} = n x^{n - 1}$
Any number that is already in front of $x$ is multiplied by the power that was brought down
- Differentiating $y = 2 x^{5}$ gives $\frac{d y}{d x} = 2 \times 5 x^{4} = 10 x^{4}$
- Differentiating $y = \frac{1}{2} x^{8}$ gives $\frac{d y}{d x} = \frac{1}{2} \times 8 x^{7} = 4 x^{7}$
- Differentiating $y = k x^{n}$ gives $\frac{d y}{d x} = k n x^{n - 1}$
Be careful with two special cases:
- Differentiating $y = k x$ gives $\frac{d y}{d x} = k$
  - The $x$ disappears leaving just a number
  - For example, $y = 2 x$ differentiates to $\frac{d y}{d x} = 2$
  - This makes sense, the gradient of the straight line $y = 2 x$ is 2
- Differentiating just a number (a constant term), $y = c$ , gives $\frac{d y}{d x} = 0$
  - Numbers disappear!
  - For example, $y = 4$ differentiates to $\frac{d y}{d x} = 0$
  - This makes sense, the gradient of the horizontal line $y = 4$ is zero

Image showing how the equation y = kx^n differentiates to dy/dx = knx^(n-1)

How do I differentiate sums and differences of terms?

The equation of a curve may include a number of different terms
- You can differentiate each term individually
  - Differentiating $y = x^{5} + x^{8}$ gives $\frac{d y}{d x} = 5 x^{4} + 8 x^{7}$
  - Differentiating $y = 4 x^{3} - 10 x^{6}$ gives $\frac{d y}{d x} = 12 x^{2} - 60 x^{5}$
Remember the two special cases of:
- $k x$ differentiating to just $k$
- and constant terms, $c$ , differentiating to zero
  - E.g. differentiating $y = 8 x + 1$ gives $\frac{d y}{d x} = 8$

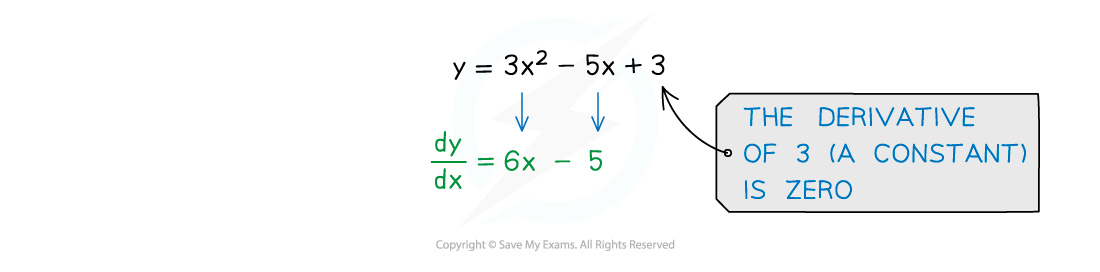
Image showing the equation y = 3x^2 - 5x + 3 differentiates to dy/dx = 6x - 5

How do I find the gradient of a curve using the gradient function?

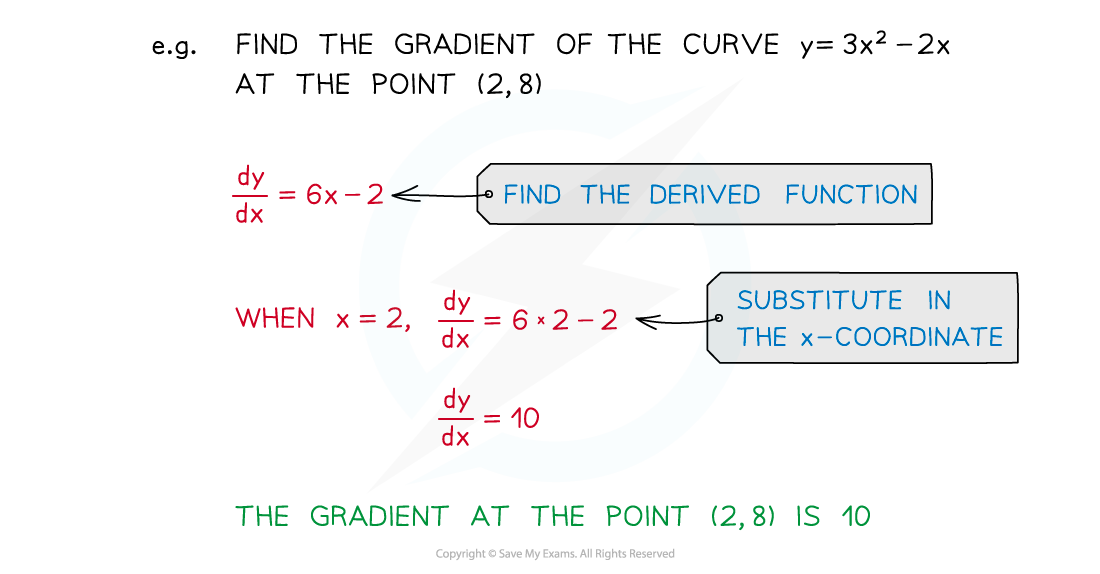
Find the x-coordinate of the point on the curve you're interested in
Use differentiation to turn the equation of the curve, $y = . . .$ , into the gradient function, $\frac{d y}{d x} = . . .$
Substitute the x-coordinate into the gradient function to find the gradient
- The y-coordinate is not needed

Image showing how the gradient of the curve y = 3x^2 - 2x at the point (2, 8), by differentiating the function and then substituting in x = 2. The gradient of the function at this (2, 8) is 10.

If instead you are given a gradient and asked to find the x-coordinate
- set $\frac{d y}{d x}$ equal to that gradient and solve the equation

Examiner Tips and Tricks

Don't forget to write the left-hand sides of $y = . . .$ and $\frac{d y}{d x} = . . .$ to avoid mixing up the curve equation with the gradient function!

The gradient of a curve changes as you move along the curve
- To find the gradient at a particular point you can draw a tangent and find its gradient
- This is a graphical method that is not accurate
  - It depends on how well you draw the tangent
Instead, you can use differentiation to find the gradient function, then substitute the x-coordinate of the point into the gradient function to find the gradient
- This is an algebraic method that is exact
For example, to find the gradient of the curve $y = x^{3} - 2 x^{2} + 6$ at the point P where $x = 2$
- either try to draw a tangent at $x = 2$ and measure its gradient (see below)
- or differentiate the equation to get $\frac{d y}{d x} = 3 x^{2} - 4 x$
  - Substitute in $x = 2$ to get $\frac{d y}{d x} = 3 \times 2^{2} - 4 \times 2 = 4$
  - The gradient is 4

Graph showing the curve with equation y = x^3 - 2x^2 + 6 and a tangent to the curve at a point P.

Worked Example

A curve has the equation $y = x^{3} - 3 x^{2} - 4 x + 1$ .

(a) Find the gradient of the curve at the point $(1, - 5)$ .

Find the gradient function using differentiation

$\begin{array}{rcl} \frac{d y}{d x} & = & 3 x^{2} - 3 \times 2 x - 4 + 0 \\ \frac{d y}{d x} & = & 3 x^{2} - 6 x - 4 \end{array}$

Substitute $x = 1$ into the gradient function

$\begin{array}{rcl} \frac{d y}{d x} & = & 3 \times 1^{2} - 6 \times 1 - 4 \\ = & - 7 \end{array}$

The gradient when $x = 1$ is -7
(The y-coordinate of the point is not needed)

The gradient at $(1, - 5)$ is -7

(b) Find the coordinates of the two points on the curve with a gradient of 5.

This is saying that $\frac{d y}{d x} = 5$
(This is not the same as substituting in $x = 5$ )

Form an equation using $\frac{d y}{d x}$ from above

$3 x^{2} - 6 x - 4 = 5$

This is a quadratic equation
Bring the terms to one side and solve (for example, by factorisation)

$\begin{array}{rcl} 3 x^{2} - 6 x - 9 & = & 0 \\ x^{2} - 2 x - 3 & = & 0 \\ (x - 3) (x + 1) & = & 0 \\ x & = & 3 or x = - 1 \end{array}$

These are the $x$ -coordinates of the two points on the curve with gradient 5
Substitute $x = 3$ into $y = x^{3} - 3 x^{2} - 4 x + 1$ to find the $y$ -coordinate of this point

$\begin{array}{rcl} y & = & 3^{3} - 3 \times 3^{2} - 4 \times 3 + 1 \\ = & - 11 \end{array}$

Similarly, substitute $x = - 1$ into the equation for $y$

$\begin{array}{rcl} y & = & {(- 1)}^{3} - 3 \times {(- 1)}^{2} - 4 \times (- 1) + 1 \\ = & 1 \end{array}$

Write out the two sets of coordinates

The points $(3, - 11)$ and $(- 1, 1)$ have a gradient of 5

Last updated: 17 October 2024

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Flashcards

Did this page help you?

Previous:Rates-of-Change GraphsNext:Finding Stationary Points & Turning Points

Differentiation (Cambridge (CIE) IGCSE Maths)

Revision Note

Differentiation

What is a gradient function?

What is differentiation and how does it work?

How do I differentiate sums and differences of terms?

How do I find the gradient of a curve using the gradient function?

How is the gradient function related to drawing tangents?

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

Number

Number Toolkit

Types of Numbers

Irrational Numbers

Negative Numbers

Mathematical Symbols

Order of Operations (BIDMAS/BODMAS)

Addition & Subtraction

Multiplication & Division

Operations with Decimals

Set Notation & Venn Diagrams

Set Notation & Venn Diagrams

Prime Factors, HCF & LCM

Prime Factor Decomposition

Uses of Prime Factor Decomposition

HCF & LCM

Powers, Roots & Standard Form

Powers & Roots

Laws of Indices

Converting to & from Standard Form

Operations with Standard Form

Fractions Toolkit

Basic Fractions

Mixed Numbers & Improper Fractions

Adding & Subtracting Fractions

Multiplying & Dividing Fractions

Percentages Toolkit

Basic Percentages

Percentage Increases & Decreases

Reverse Percentages

Simple & Compound Interest, Growth & Decay

Simple Interest

Compound Interest

Depreciation

Exponential Growth & Decay

Surds

Simplifying Surds

Rationalising Denominators

Working with FDP

Converting Fractions, Decimals & Percentages

Recurring Decimals

Ordering Fractions, Decimals & Percentages

Working with Ratios

Ratios

Problem Solving with Ratios

Working with Proportion

Compound Measures (Speed, Density, Pressure)

Compound Measures

Speed, Density & Pressure

Time, Currency & Conversions

Time

Money Calculations

Exchange Rates

Rounding, Estimation & Bounds

Rounding & Estimation

Upper & Lower Bounds

Using a Calculator

Using a Calculator

Algebra & Sequences

Algebra Toolkit

Algebraic Notation

Algebraic Vocabulary

Substitution

Collecting Like Terms

Algebraic Roots & Indices

Algebraic Roots & Indices

Expanding & Factorising Brackets

Expanding & Simplifying Single Brackets

Expanding Double Brackets