Quadratic Graphs (Cambridge (CIE) IGCSE Maths): Revision Note
Exam code: 0580 & 0980
Quadratic graphs
What is a quadratic graph?
A quadratic graph has the form
where
is not zero
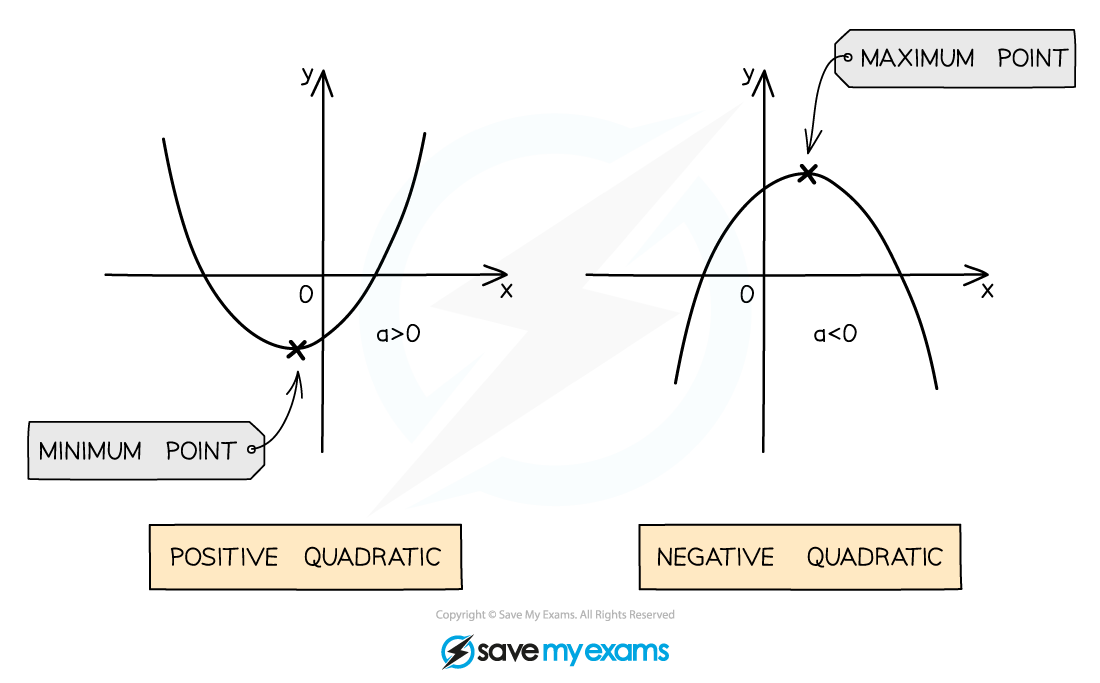
What does a quadratic graph look like?
A quadratic graph is a smooth curve with a vertical line of symmetry
A positive number in front of
gives a u-shaped curve
A negative number in front of
gives an n-shaped curve
The shape made by a quadratic graph is known as a parabola
A quadratic graph will always cross the
-axis
A quadratic graph crosses the
-axis twice, once, or not at all
The points where the graph crosses the
-axis are called the roots
If the graph is a u-shape, it has a minimum point
If the graph is an n-shape, it has a maximum point
Minimum and maximum points are both examples of turning points
A turning point can also be called a vertex
How do I sketch a quadratic graph?
It is important to know how to sketch a quadratic curve
A simple drawing showing the key features is often sufficient
(For a more accurate graph, create a table of values and plot the points)
To sketch a quadratic graph:
First sketch the
and
-axes
Identify the
-intercept and mark it on the
-axis
The
-intercept of
will be
It can also be found by substituting in
Find all root(s) (0, 1 or 2) of the equation and mark them on the
-axis
The roots will be the solutions to
;
You can find the solutions by factorising, completing the square or using the quadratic formula
Identify if the number
in
is positive or negative
A positive value will result in a u-shape
A negative value will result in an n-shape
Sketch a smooth curve through the
and
-intercepts
Mark on any axes intercepts
Mark on the coordinates of the maximum/minimum point if you know it
How do I find the coordinates of the turning point by completing the square?
The coordinates of the turning point (vertex) of a quadratic graph can be found by completing the square
For a quadratic graph written in the form
the minimum or maximum point has coordinates
Beware: there is a sign change for the
-coordinate
A curve with equation
, has a minimum point at
A curve with equation
, has a minimum point at
The value of
does not affect the coordinates of the turning point but it will change the shape of the graph
If it is positive, the graph will be a u-shape
The curve
has a minimum point at
If it is negative, the graph will be an n-shape
The curve
has a maximum point at
How do I find the coordinates of the turning point using differentiation?
The coordinates of the turning point (maximum/minimum) of a quadratic can be found through differentiation
To find the coordinates of the turning point
Differentiate the quadratic equation
This will give you
Set
and solve for
The solution will be the
-coordinate of the turning point
Substitute the
value into
This will give you the
-coordinate of the turning point
Worked Example
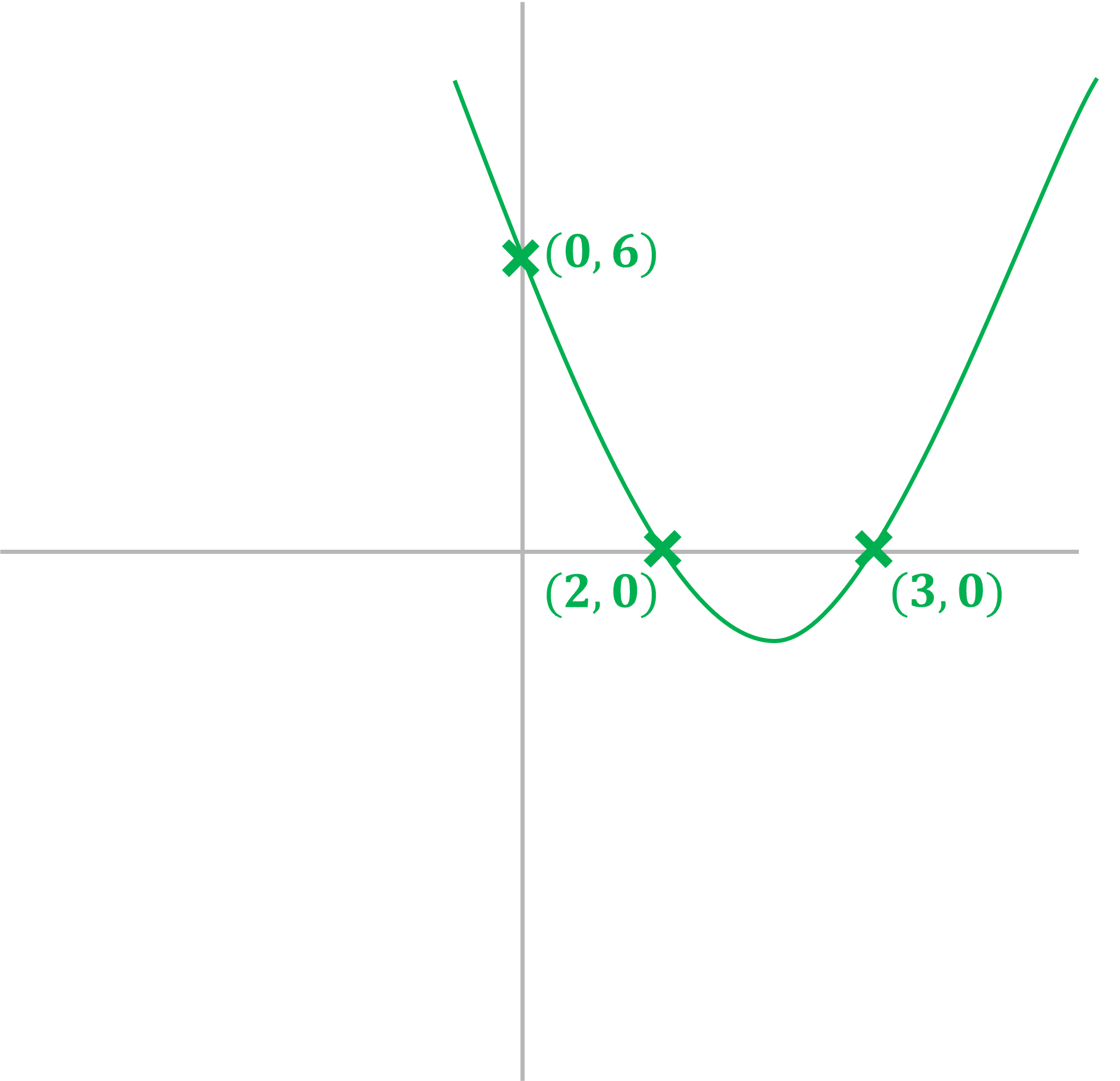
(a) Sketch the graph of showing the
and
intercepts clearly.
Answer:
The at the end is the
-intercept
-intercept: (0, 6)
Factorise the quadratic expression
Solve
So the x-intercepts are given by the coordinates
(2, 0) and (3, 0)
It is a positive quadratic graph, so will be a u-shape
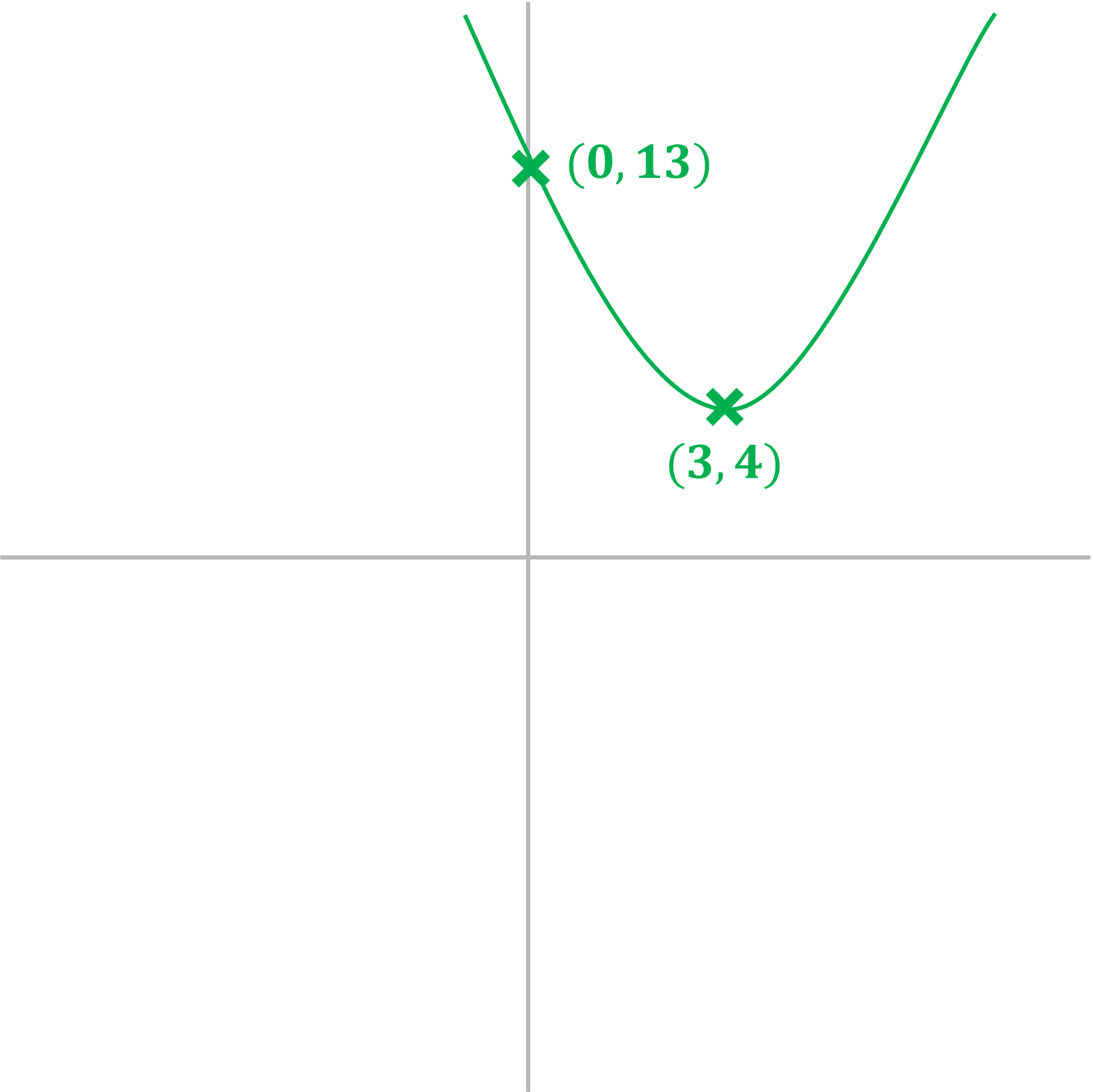
(b) Sketch the graph of showing the
-intercept and the coordinates of the turning point.
Answer:
It is a positive quadratic, so will be a u-shape
The turning point will therefore be a minimum
The at the end is the
-intercept
-intercept: (0, 13)
Find the minimum point by completing the square (or through differentiation)
For example, complete the square by writing the equation in the form (you may need to look this method up)
The turning point of has coordinates
The minimum point is therefore
(3, 4)
As the minimum point is above the -axis, and the curve is a u-shape, this means the graph will not cross the
-axis (it has no roots)
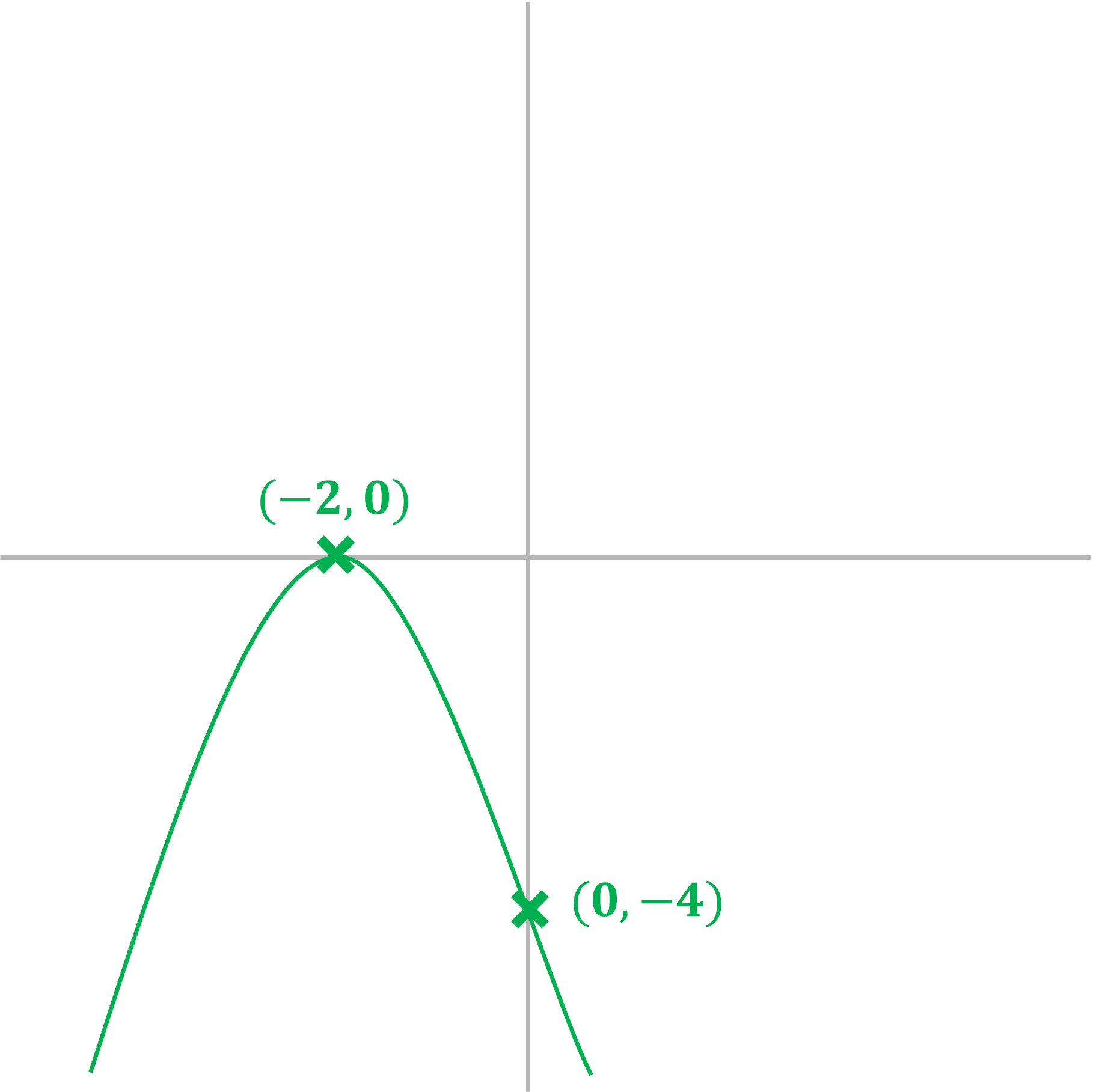
(c) Sketch the graph of showing the root(s),
-intercept, and the coordinates of the turning point.
Answer:
It is a negative quadratic, so will be an n-shape
The turning point will therefore be a maximum
The at the end is the
-intercept
-intercept: (0, -4)
Find the minimum point by completing the square or through differentiation
For example, differentiate the equation
Set the derivative equal to zero and solve for
Substitute this value of back into the original equation for
This shows that the maximum point has coordinates
(-2, 0)
As the maximum is on the -axis, there is only one root
How do I find the equation of a quadratic from its graph?
If the vertex and one other point are known
Use the form
to fill in
and
The vertex is at
Then substitute in the other known point
to find
If the roots (
-intercepts) and one other point are known
Use the form
to fill in
and
The roots are at
and
Then substitute in the other known point
to find
If
then you only need either the vertex or the roots
Worked Example
(a) Find the equation of the graph below.
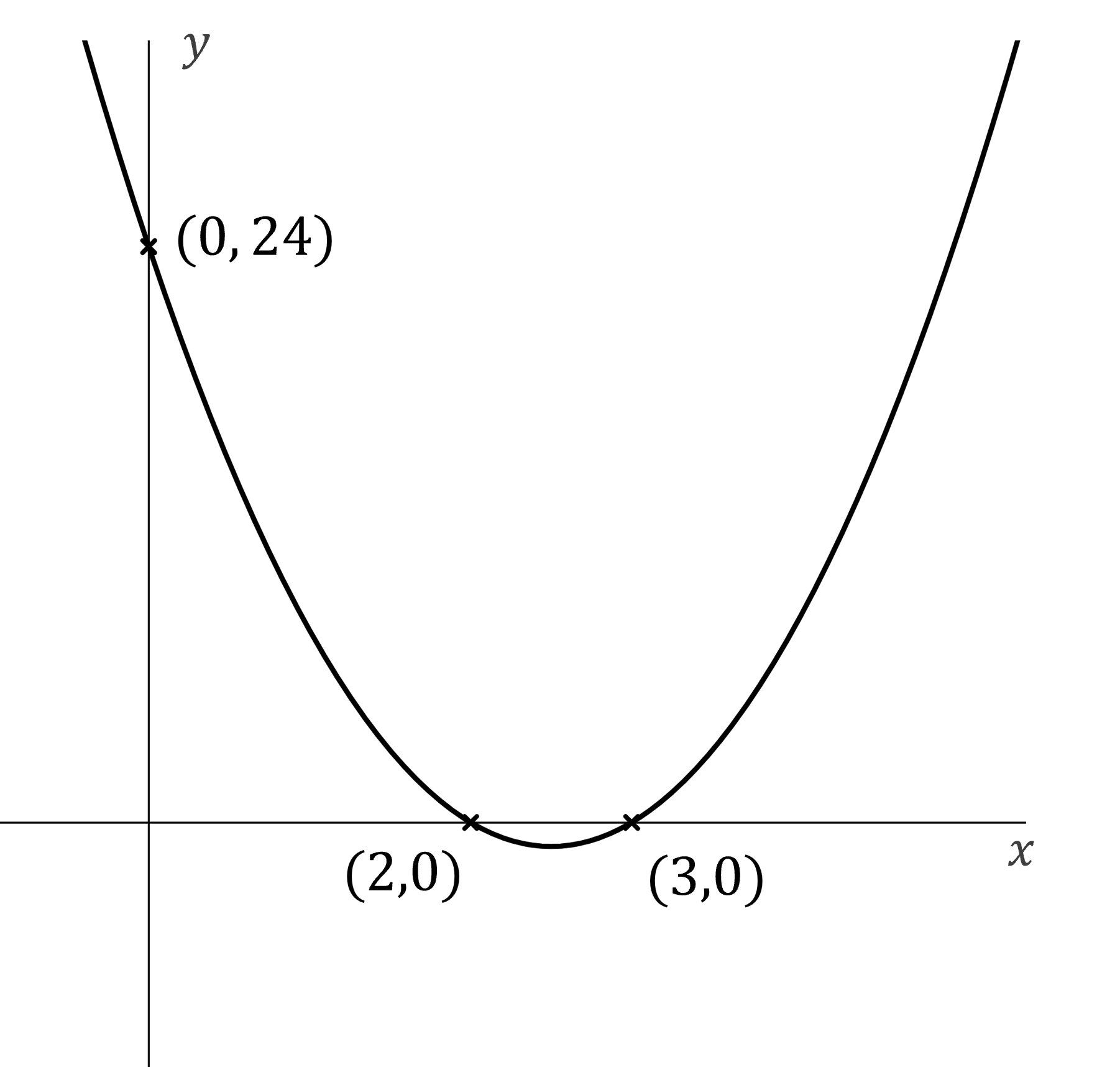
Answer:
The graph shows the roots and a point on the curve (in this case the -intercept)
Use the form to fill in
and
by inspection
The roots are at and
Substitute in the other known point (0, 24) to find
Write the full equation
You could also write this in expanded form:
(b) Find the equation of the graph below.
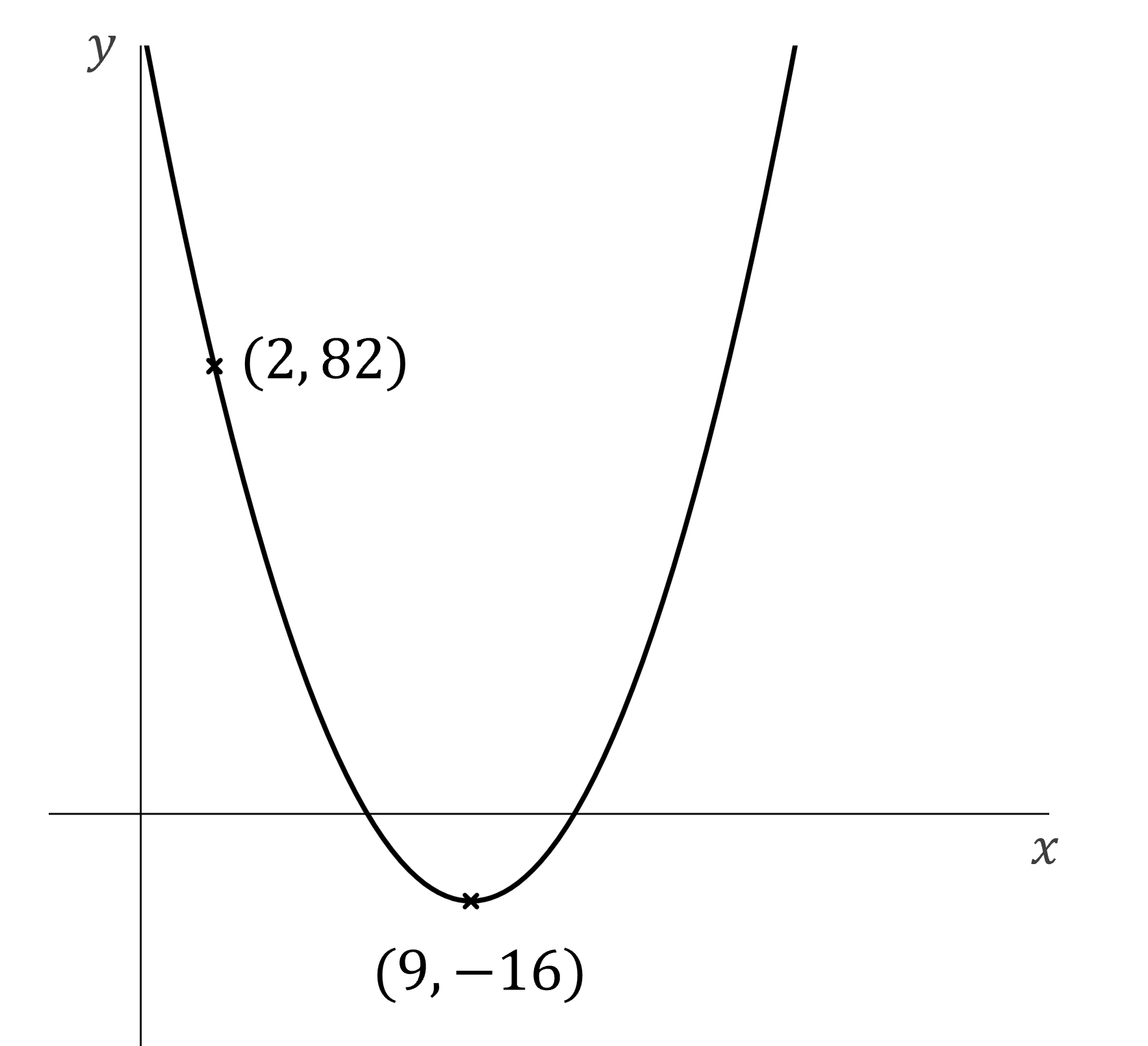
Answer:
The graph shows the vertex and a point on the curve
Use the form to fill in
and
by inspection
The vertex is at
Substitute in the other known point (2, 82) to find
Write the full equation
You could also write this in expanded form:

Unlock more, it's free!
Did this page help you?