Introduction to Functions (Cambridge (CIE) IGCSE Maths)

Introduction to Functions

What is a function?

• A function is a combination of one or more mathematical operations that takes a set of numbers and changes them into another set of numbers

• The numbers being put into the function are often called the inputs

• The numbers coming out of the function are often called the outputs

• A function may be thought of as a mathematical “machine”

  • For example, for the function “double the number and add 1”, the two mathematical operations are "multiply by 2 (×2)" and "add 1 (+1)"  

    • Putting 3 in to the function would give 2 × 3 + 1 = 7

    • Putting -4 in would give 2 × (-4) + 1 = -7 

    • Putting in would give

What is function notation?

• A function, f, with input can be written as

  • Letters other than f can be used

    • The letters g, h and j are common but any letter can be used

    • Typically, a new letter will be used to define a new function in a question

• For example, the function with the rule “triple the number and subtract 4” would be written

  •  

• In such cases, "" is the input and "" is the output

• Sometimes functions don’t have names like f and are just written as y = …

  • E.g. 

How does a function work?

• A function has an input and an output 

  • If the input is 2, then the output is

  • If the input is , then the output is

  • If the input is , then the output is

    • You cannot simplify this output any further

• If the function is known, the output can be calculated

  • For example, given the function 

    • 

    • 

    • 

• If the output is known, an equation can be formed and solved to find the input

  • For example, given the function 

    • If , then form an equation by replacing with

    • 

    • Solving this equation gives an input of 7

• Note that and are very different things:

  • means an input of gives an output of 15

  • means substitute the input 15 into the function

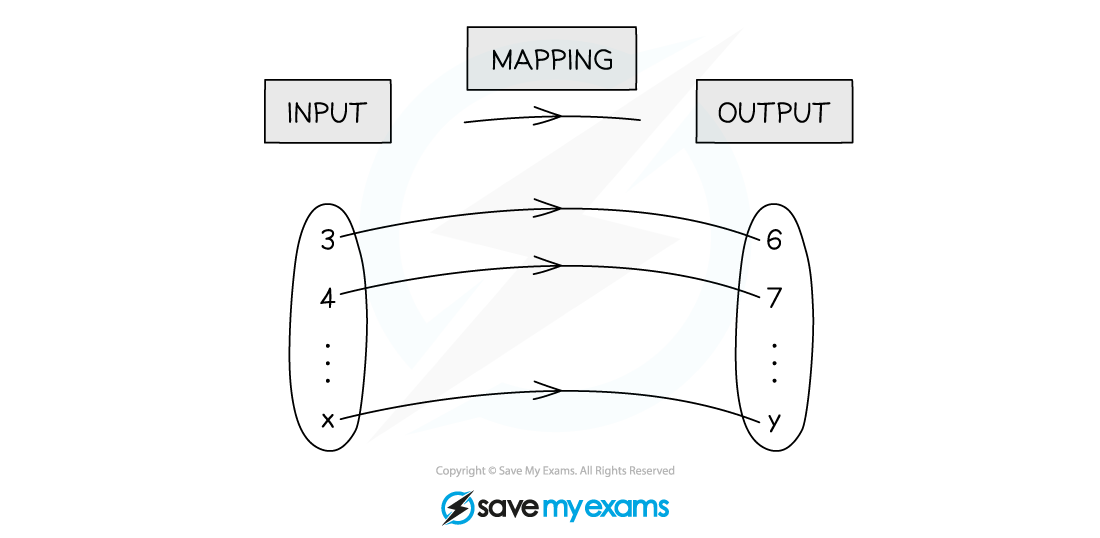
What is a mapping diagram?

• A mapping diagram shows a set of different inputs going into the function to become a set of different outputs

  • Transforming inputs into outputs is called mapping

• For example, a mapping diagram for the function  where could be shown as: