Set Notation & Venn Diagrams | CIE IGCSE Maths: Core Revision Notes 2025

Set Notation

What is a set?

A set is a collection of elements
- Elements could be anything
  - Numbers, letters, coordinates, ...
You could describe a set by writing its elements inside curly brackets {}
- {1, 2, 3, 6} is the set of factors of 6
If the set of elements follow a rule then you can write this using a colon inside the curly brackets {... : ...}
- The bit before the colon is the type of element
- The bit after the colon is the rule
  - {x is a positive integer : x² < 30} is the set of positive integers which, when squared, are less than 30
  - This is equal to {1, 2, 3, 4, 5}
- The colon is often read as 'such that'
- If no type is specified, x can take any value (fractions, decimals, irrationals, ...)
  - {x: x² < 30} means any value whose square is less than 30

What do I need to know about set notation?

$E$ is the universal set (the set of everything)
- For example, if we are only interested in factors of 24 then $E$ = {1, 2, 3, 4, 6, 8, 12, 24}
- You may see alternative notations used for $E$
  - U is a common alternative (different to $\cup$ for union!)
  - S or the Greek letter ξ (xi) may also be seen
We use upper case letters to represent sets (A, B, C, ...) and lower case letters to represent elements (a, b, c, ...)
n(A) is the number of elements in set A
- For example, if $E$ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, A = {1, 4, 9}, B = {1, 2, 3, 4, 5, 6}
  n(A) = 3, n(B) = 6
A B means the intersection of A and B (the overlap of A and B)
- This is the set of elements that are in both set A and set B
  A $\cap$ B = {1, 4}
A B means the union of A and B (everything in A or B or both)
- This is the set of elements that are in at least one of the sets
- This includes elements in both sets (in the intersection)
  A $\cup$ B = {1, 2, 3, 4, 5, 6, 9}
A' means the complement of A
- It is the set of all elements in the universal set $E$ that are not in A
  A' = {2, 3, 5, 6, 7, 8, 10}

Sets & Venn Diagrams

What is a Venn diagram?

A Venn diagram is a way to illustrate all the elements within sets and any intersections
A Venn diagram consists of
- a rectangle representing the universal set ( $E$ )
- a circle for each set
  - Circles may or may not overlap depending on which elements are shared between sets

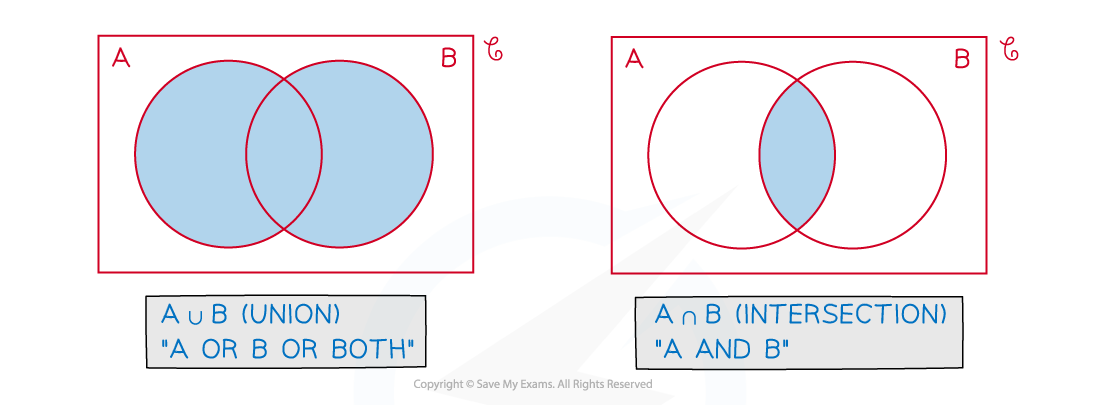
What do the different regions mean on a Venn diagram?

$A \cap B$ is represented by the region where the A and B circles overlap
$A \cup B$ is represented by the regions that are in A or B or both

Venn diagrams showing the union and the intersection of sets A and B

Worked example

Two sets A and B are shown in the Venn diagram.

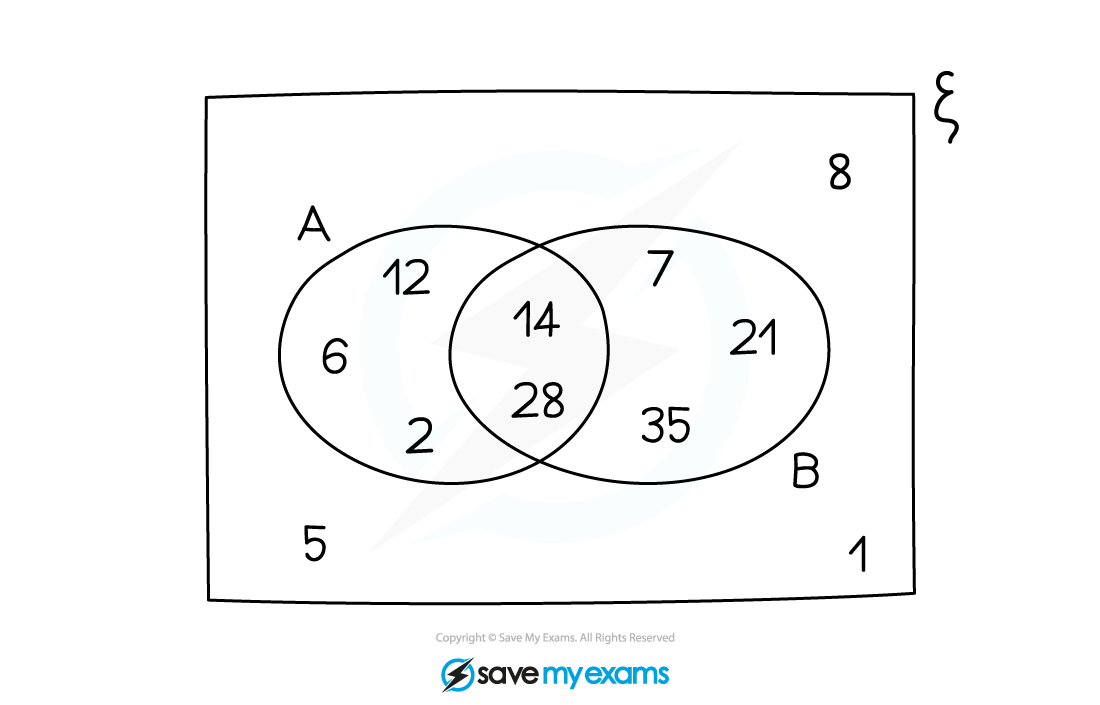
Two sets, A and B, represented on a Venn diagram

(a)

Write down n(A).

The elements of A are anything inside the A circle

A = {2, 6, 12, 14, 28}

n(A) means the number of elements in A
There are 5 elements in A

n(A) = 5

(b)

Use set notation to complete the sentence {14, 28} = ...

14 and 28 are the elements that are both in A and B
This means they are in the intersection of A and B

{14, 28} = A ∩ B

(c)

Write down the elements that are in set A U B.

A = {2, 6, 12, 14, 28} and B = {7, 14, 21, 28, 35}
A U B is the set of elements that are in at least one of the sets
For elements in both, only write them out once

A U B = {2, 6, 7, 12, 14, 21, 28, 35}

Set Notation & Venn Diagrams (CIE IGCSE Maths: Core)

Revision Note

Set Notation

What is a set?

What do I need to know about set notation?

Sets & Venn Diagrams

What is a Venn diagram?

What do the different regions mean on a Venn diagram?

Worked example

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Mark