Compound Measures (CIE IGCSE Maths: Core)

What is a compound measure?

• A compound measure is something that is calculated by using more than one measurement
• Compound measures can be used to measure rates
• This measures how much one quantity changes when the other is increased by 1
• Examples include:
• Speed – how much the distance changes for each unit of time
• Flow rate – how much the volume changes for each unit of time
• Population density – how many people there are for each unit of area
• Fuel consumption - volume of  fuel used for each unit of distance travelled

How do I find the units for a compound measure?

• You can use the formula for a compound measure to derive its units
  • Use the units for the quantities in the formula to derive the units of the compound measure
  • Write a division as a/b or ab^-1 and pronounce it as “a per b”
• Examples include:
  • 
    • If the distance is measured in km and the time is measured in minutes then the speed is measured in km/min or km min^-1
  • 
    • If the volume is measured in m³ and the time is measured in minutes then the flow rate is measured in m³/min or m³min^-1

How do I find the formula for a compound measure?

• You can use the units for a compound measure to help remember its formula
  • You just need to remember what each unit measures
  • If the unit is a/b then the formula will be the quantity that a measures divided by the quantity that b measures
• Examples include:
  • Density can be measured in kg/cm³
  • kg is a measure of mass and cm³ is a measure of volume
  • Therefore 

What is a formula triangle?

• A formula triangle shows the relationship between the different measures in a compound formula 
  • E.g. for Speed, Distance and Time

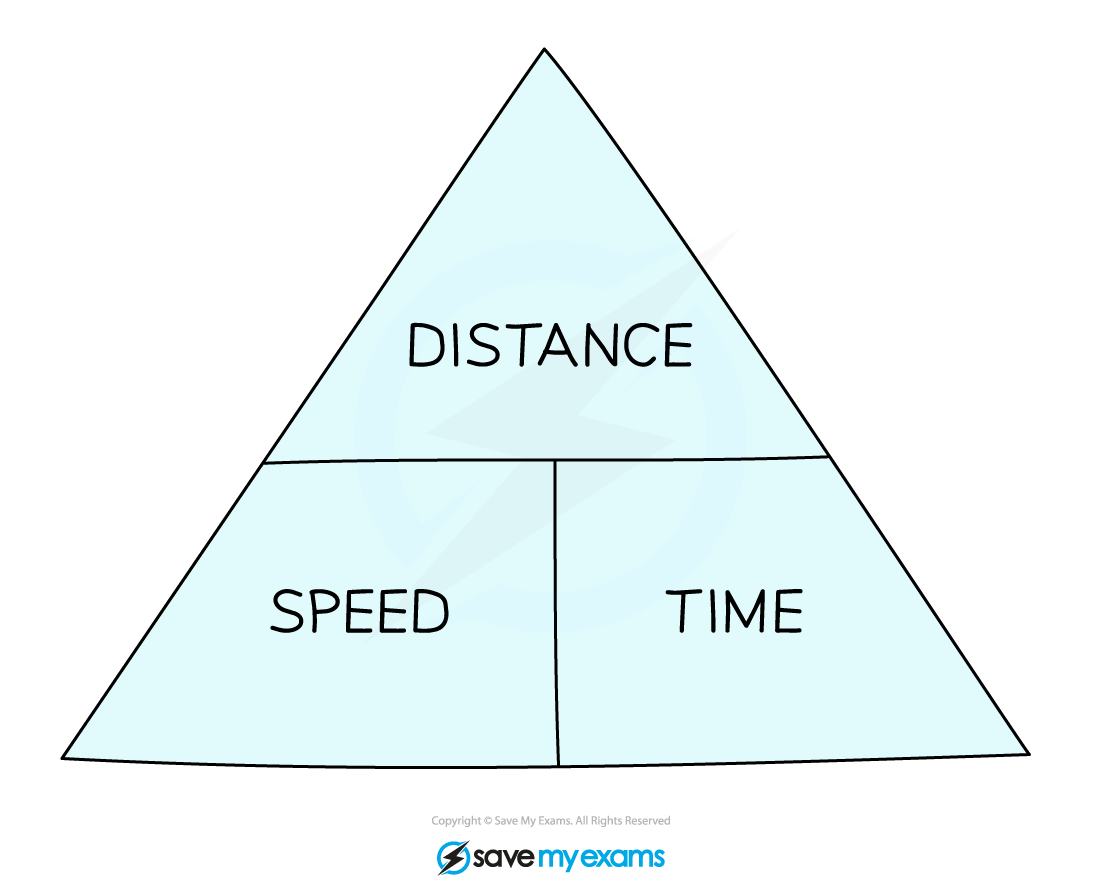
• • If you are calculating a variable on the top of the triangle, multiply the two variables on the bottom
    • For example,   
  • If you are calculating a variable on the bottom of the triangle, divide the top by the other variable on the bottom
    
    • For example,    and 

What are speed, density and pressure?

• Speed, density and pressure are frequently used compound measures
  • Speed is equal to distance divided by time
  • Density is equal to mass divided by volume
  • Pressure is equal to force divided by area

What should I know about speed, distance and time?

• Speed is commonly measured in metres per second (m/s) or kilometres per hour (km/h)
  
  • The units indicate speed is distance per time
    
• 'Speed' (in this formula) means 'average speed'
• In harder problems there are often two journeys or two parts to one longer journey

What should I know about density, mass and volume?

• Density is usually measured in grams per centimetre cubed (g/cm³) or kilograms per metre cubed (kg/m³)
  • The units indicate that density is mass per volume
    

• You may need to use a volume formula to find the volume of an object first

What should I know about pressure, force and area?

• Pressure is usually measured in Newtons per square metre (N/m²)
  • The units of pressure are often called Pascals (Pa) rather than N/m²
  • The units indicate that pressure is force per area
    
• Remember that weight is a force
  • It is different to mass