Arc Lengths & Sector Areas (Cambridge (CIE) IGCSE Maths) : Revision Note
Did this video help you?
Arc Lengths & Sector Areas
What is an arc?
An arc is a part of the circumference of a circle
Two points on a circumference of a circle will create two arcs
The smaller arc is known as the minor arc
The bigger arc is known as the major arc
What is a sector?
A sector is the part of a circle enclosed by two radii (radiuses) and an arc
A sector looks like a slice of a circular pizza
The curved edge of a sector is the arc
Two radii in a circle will create two sectors
The smaller sector is known as the minor sector
The bigger sector is known as the major sector
What formulae do I need to know?
You need to be able to calculate the length of an arc and the area of a sector
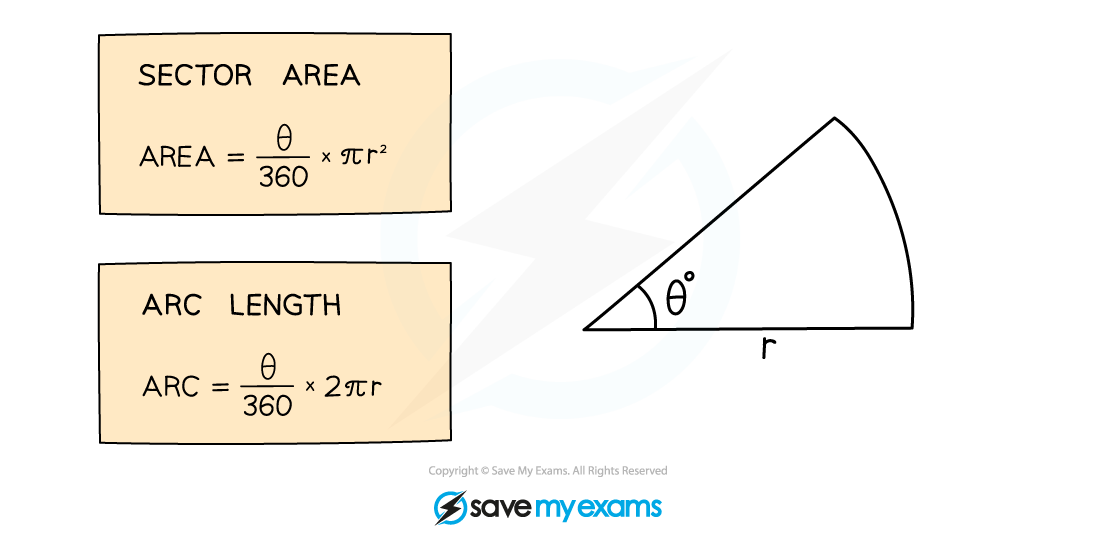
The angle formed in a sector by the two radii is often labelled θ (the Greek letter “theta”)
You can calculate the area of a sector or the length of an arc by adapting the formulae for the area or circumference of a circle
A full circle is equal to 360° so the fraction will be the angle, θ°, out of 360°
Working with sector and arc formulae is just like working with any other formula:
Write down what you know (or what you want to know)
Pick the correct formula
Substitute the values in and solve
How do I find the length of an arc?
STEP 1
Divide the angle by 360 to form a fractionSTEP 2
Calculate the circumference of the full circleSTEP 3
Multiply the fraction by the circumference
How do I find the area of a sector?
STEP 1
Divide the angle by 360 to form a fractionSTEP 2
Calculate the area of the full circleSTEP 3
Multiply the fraction by the area
Examiner Tips and Tricks
The area and circumference of a circle formulae are given to you in the exam.
You just need to remember how to find the correct fraction of the whole circle.
Worked Example
A sector of a circle is shown.
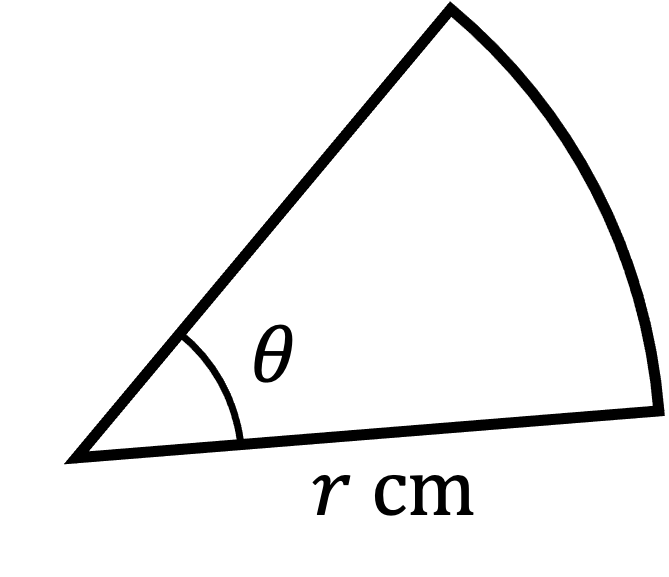
The angle, θ, is 72° and the radius, r, is 5 cm.
(a) Find the area of the sector, giving your answer correct to 3 significant figures.
Substitute θ = 72° and r = 5 into the formula for the area of a sector,
Use a calculator to work out this value
15.70796...
Round your answer to 3 significant figures
15.7 cm2
(b) Find the length of the arc of the sector, giving your answer as a multiple of .
Substitute θ = 72° and r = 5 into the formula for the length of an arc,
Simplify the number part without
Write down the final answer with
2π cm

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?

