Tangent & Radius

What is a tangent?

A tangent to a circle is a straight line outside of the circle that touches its circumference only once

Circle Theorem: A radius and a tangent are perpendicular

This circle theorem states that a radius and a tangent meet at right angles (90°)
- This may also be described as being perpendicular to each other
When using this theorem in an exam you must use the keywords
- A radius and a tangent meet at right angles (or 90°)

Radius and tangent are perpendicular circle theorem

Examiner Tip

If you spot a tangent on a circle diagram, look to see if it meets a radius and label the right angle on the diagram
- In some cases just doing this can earn you a mark!
If you think you have spotted this circle theorem in a question, make sure it is a radius that meets the tangent, and not a chord
- A radius passes through the centre of the circle

Worked example

P and Q are points on the circle, centre O.

APB is a tangent to the circle at P.

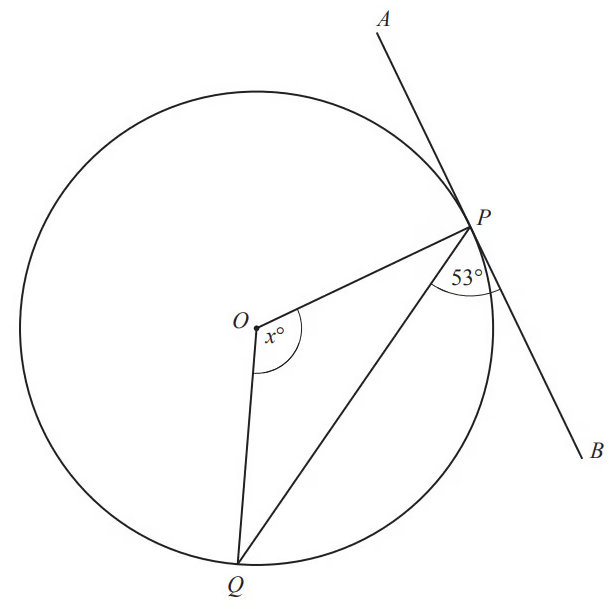
tangent-and-radius-diagram-worked-example

(i)

Explain why angle OPB is 90°.

(ii)

Find the value of

x .

(i)

Angle OPB is 90° because the angle between a tangent and a radius is 90° (and OP is a radius, and APB is a tangent).

(ii)

As angle OPB is 90°, we can find angle OPQ

OPQ = 90 - 53 = 37°

As OP and OQ are both the radius of the circle, they have the same length. This means the triangle OPQ is isosceles, so the base angles (OPQ and OQP) are equal

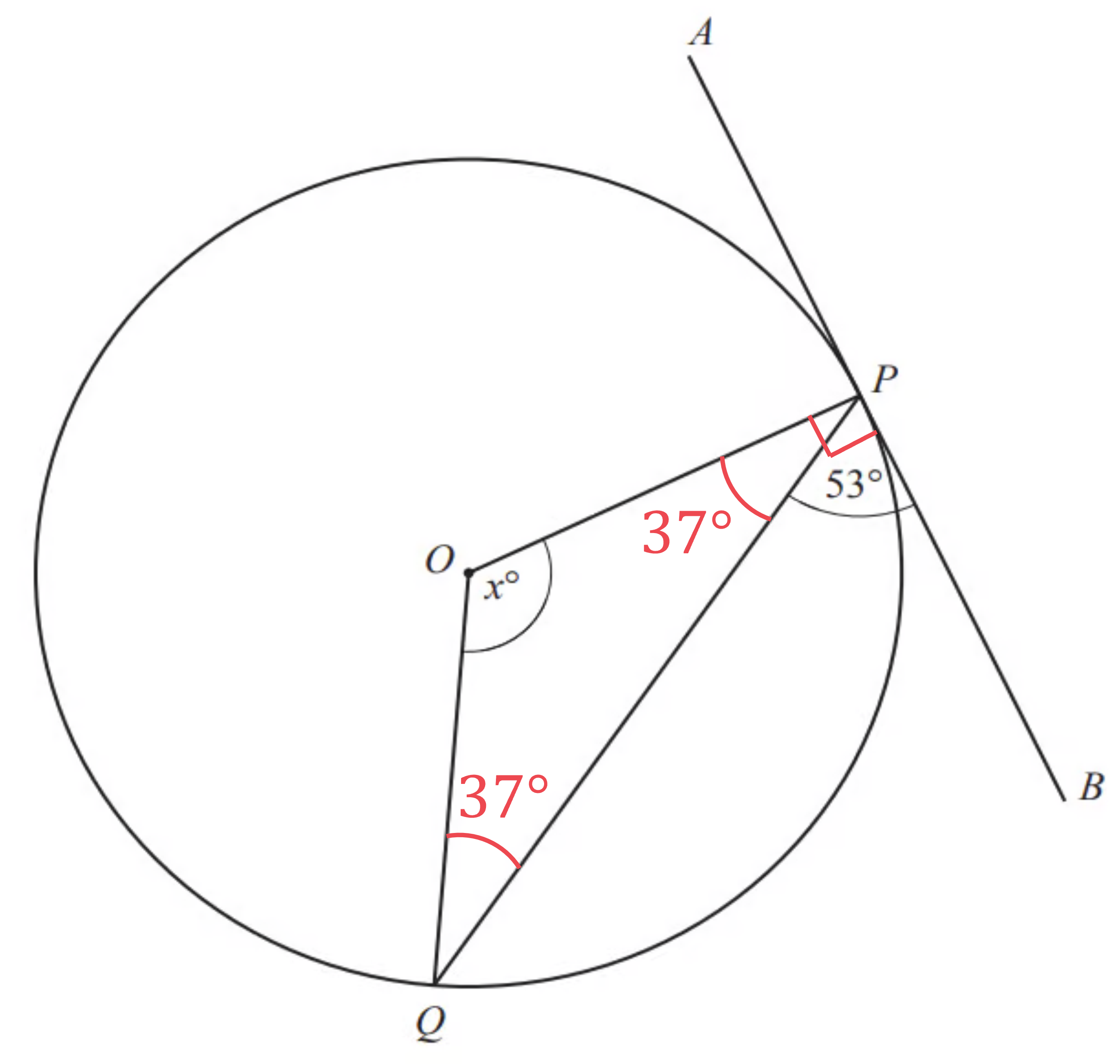
cie-igcse-core-rn-tangent-and-radius-diagram-worked-example-2-working

Using the fact that the internal angles in a triangle sum to 180, we can find angle

x

\begin{array}{rcl} x + 37 + 37 & = & 180 \\ x + 74 & = & 180 \end{array}

x = 106

Tangent & Radius (CIE IGCSE Maths: Core)

Revision Note

Tangent & Radius

What is a tangent?

Circle Theorem: A radius and a tangent are perpendicular

Examiner Tip

Worked example

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Jamie W