Angle in a Semicircle (Cambridge (CIE) IGCSE Maths): Revision Note
Exam code: 0580 & 0980
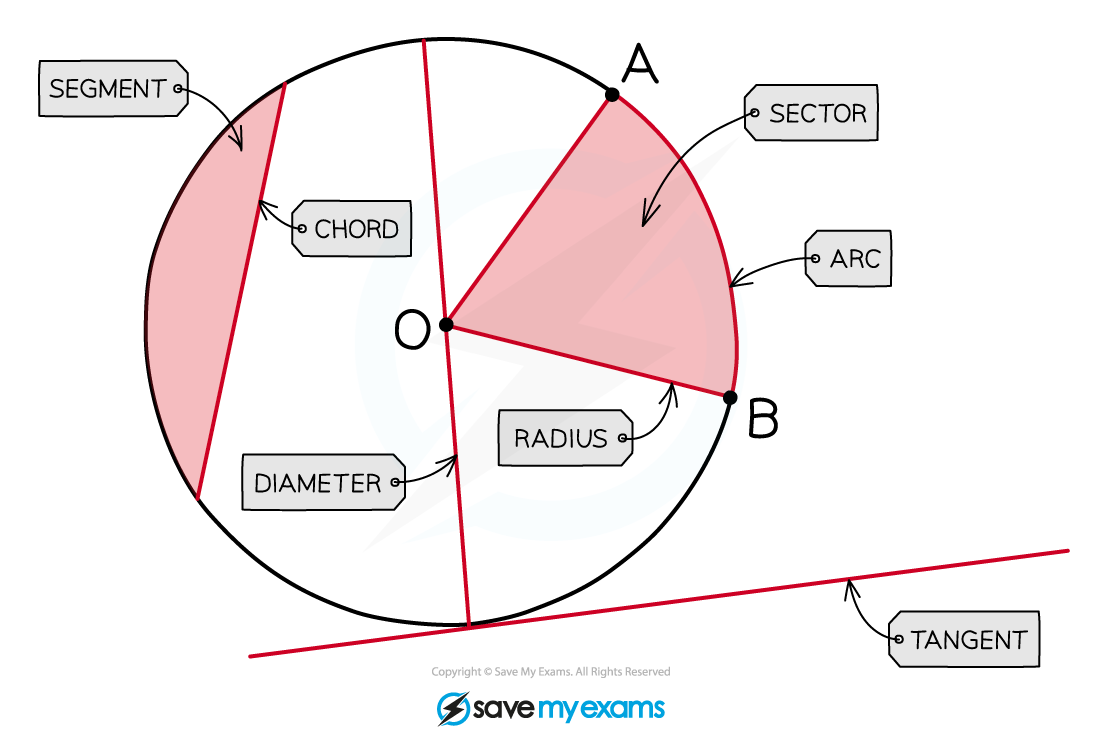
Angle in a Semicircle
What are circle theorems?
Circle Theorems deal with angles that occur when lines are drawn within (and connected to) a circle
You may need to use other facts and rules such as:
basic properties of lines and angles
properties of triangles and quadrilaterals
angles in parallel lines or polygons
Circle Theorem: The angle in a semicircle is 90°
The lines drawn from a point on the circumference to either end of a diameter are perpendicular
The angle at that point on the circumference is 90°
This circle theorem only uses half of the circle
The right-angle is called the angle in a semicircle

To spot this circle theorem on a diagram look for a triangle where
one side is the diameter
Remember that a diameter always goes through the centre
all three vertices are on the circumference
The 90º angle will always be the angle opposite the diameter
When explaining this theorem in an exam you must use the keywords:
The angle in a semicircle is 90°
Questions that use this theorem may
appear in whole circles or in semicircles
require the use of Pythagoras' Theorem to find a missing length
Examiner Tips and Tricks
As soon as you spot this arrangement in a question, mark the angle as 90° degrees on the diagram
Sometimes just doing this will earn you a mark!
Worked Example
A, B, and C are points on a circle. AC is a diameter of the circle. Find the value of a.
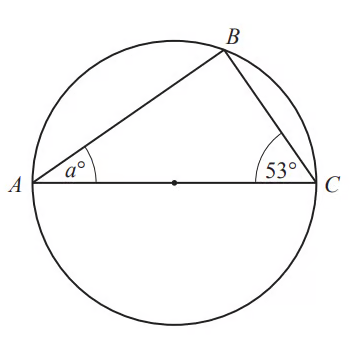
As the line AC is the diameter of the circle, use the circle theorem "the angle in a semicircle is 90°" to state that angle B must be 90°
We can now use the fact that the internal angles of a triangle sum to 180°, to find the unknown angle
a + 53 + 90 = 180
a + 143 = 180
a = 37

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?