Distance-Time & Speed-Time Graphs | CIE IGCSE Maths: Core Revision Notes 2025

Distance-Time Graphs

How do I use a distance-time graph?

Distance-time graphs show the distance travelled at different times
- Distance is on the vertical axis
- Time is on the horizontal axis
The gradient of the graph is the speed
- $speed = \frac{distance}{time} = \frac{rise}{run}$
The steeper the line the faster the object is moving
- Lines with positive gradients represent objects moving away from the start point
- Lines with negative gradients represent objects moving towards the start point
- Lines that are horizontal represent rest
  - The object is stationary (not moving)

How do I work out the overall average speed?

For journeys with multiple parts
- the overall average speed for the whole journey is $\frac{total distance travelled}{total time}$
- The total time includes any rests

Examiner Tip

These questions often have a lot of parts that depend on each other, so always double check each answer before continuing.

Worked example

One afternoon, Mary cycled 8 km from her home to her grandfather's house.
Part of the travel graph for her journey is shown.

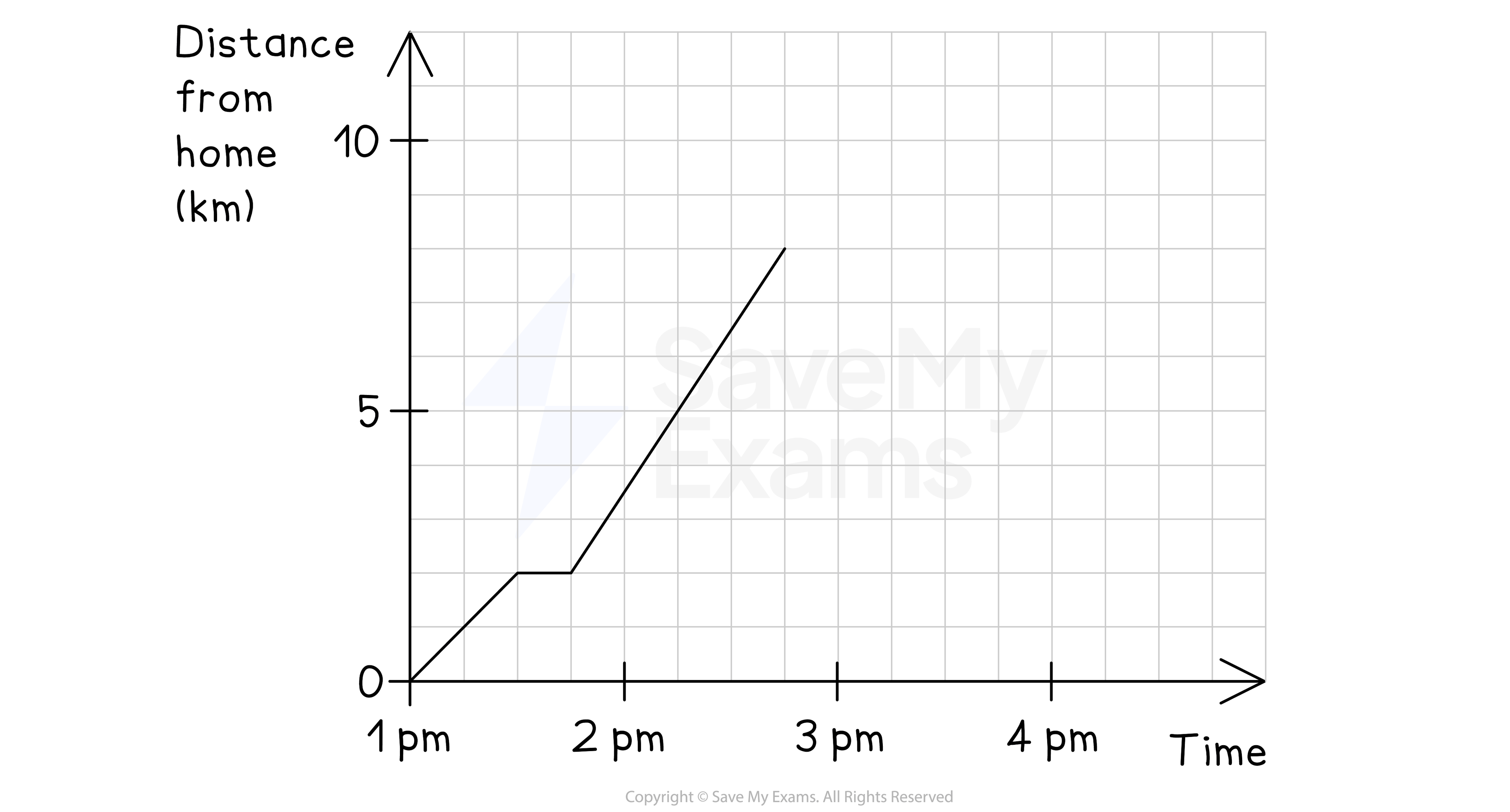
A distance time graph

(a)

Find Mary's speed at 2 pm.

The speed is the gradient of the line at that point
The gradient at 2pm is the same as the gradient for all points between 1:45pm and 2:45pm
It is easiest to use

\frac{rise}{run}

for that bigger section

\frac{rise}{run} = \frac{6}{1}

6 km/h

(b)

Calculate, in minutes, how long Mary stopped on the way to her grandfather's house.

The horizontal line is where Mary stops
The scale is 1 square = 15 minutes

15 minutes

(c)

Calculate Mary's overall average speed from leaving her home to arriving at her grandfather's house, giving your answer correct to 3 significant figures.

Overall average speed is

\frac{total distance travelled}{total time}

Total distance travelled is 8 km

Total time (including rests) is 1.75 hours

$\frac{8}{1.75} = 4.57142 . . .$

Round the answer to 3 significant figures

4.57 km/h (to 3 s.f.)

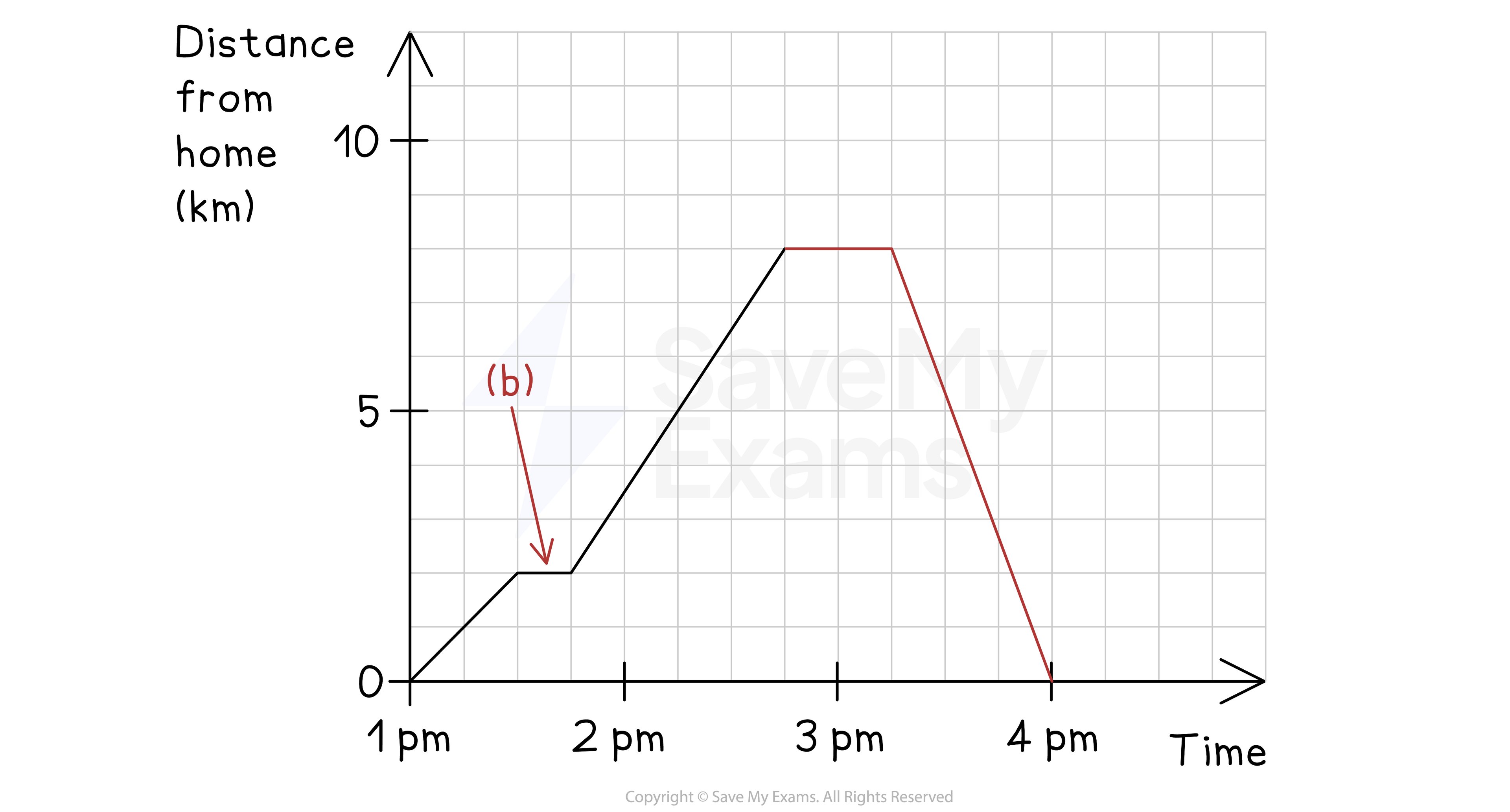
(d)

Mary stayed at her grandfather's house for half an hour, then cycled home at a steady speed without stopping, arriving home at 4pm.

Complete the travel graph for Mary's journey.

Rest is a horizontal line
Returning home is a straight line with a negative gradient

Example-5-3-20-Diagram-2, IGCSE & GCSE Maths revision notes

Speed-Time Graphs

How do I use a speed-time graph?

Speed-time graphs show the speed of an object at different times
- Speed is on the vertical axis
- Time is on the horizontal axis
Straight lines
- with positive gradients represent objects speeding up (accelerating)
- with negative gradients represent objects slowing down (decelerating)
Horizontal lines indicate moving at a constant speed
- The object is neither speeding up or slowing down
- If the constant speed is zero, then it at rest

Examiner Tip

Always check the vertical axis to see if you are given a speed-time graph or a distance-time graph!

Worked example

The speed-time graph for a car travelling between two sets of traffic lights is shown.

A speed-time graph

For how long was the car travelling at a constant speed?

Constant speed is represented by horizontal lines

There is a horizontal line from 6 seconds to 15 seconds

15 - 6 = 9

9 seconds

Distance-Time & Speed-Time Graphs (CIE IGCSE Maths: Core)

Revision Note

Distance-Time Graphs

How do I use a distance-time graph?

How do I work out the overall average speed?

Examiner Tip

Worked example

Speed-Time Graphs

How do I use a speed-time graph?

Examiner Tip

Worked example

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Mark