IGCSEMaths: CoreCIERevision NotesCoordinate Geometry & GraphsLinear GraphsCoordinate Geometry

Syllabus Edition

First teaching 2023

First exams 2025

|

Coordinate Geometry (CIE IGCSE Maths: Core)

Revision Note

Test yourself
Mark

Author

Mark

Last updated

2D Coordinates

What is the Cartesian plane?

  • The Cartesian plane is a two-dimensional grid that has
    • a horizontal scale, called the x-axis
    • a vertical scale, called the y-axis
  • The two axes meet at the origin
    • where x  and y  are both 0

What are coordinates?

  • Coordinates are a pair of numbers, x  and y , that describe the location of a point on the grid
    • They are written in brackets as (x , y )
    • The point is
      • x  units on the horizontal scale
      • y  units on the vertical scale
  • The origin is (0, 0)
    • Positive values of x  are to the right of the origin
      • Negative values are to the left
    • Positive values of y  are above the origin
      • Negative values are below
  • For example, from the origin:
    • (2, 5) is the point 2 units to the right and 5 units up
    • (-1, -4) is the point 1 unit to the left and 4 units down
  • "Along the corridor, up the stairs" helps to remember horizontal then vertical, (x , y )

Examiner Tip

  • Check the scale on the coordinate grid!
    • 1 square might not be 1 unit.

Worked example

(a)
Write down the coordinates of the point A shown on the axes below. 
 

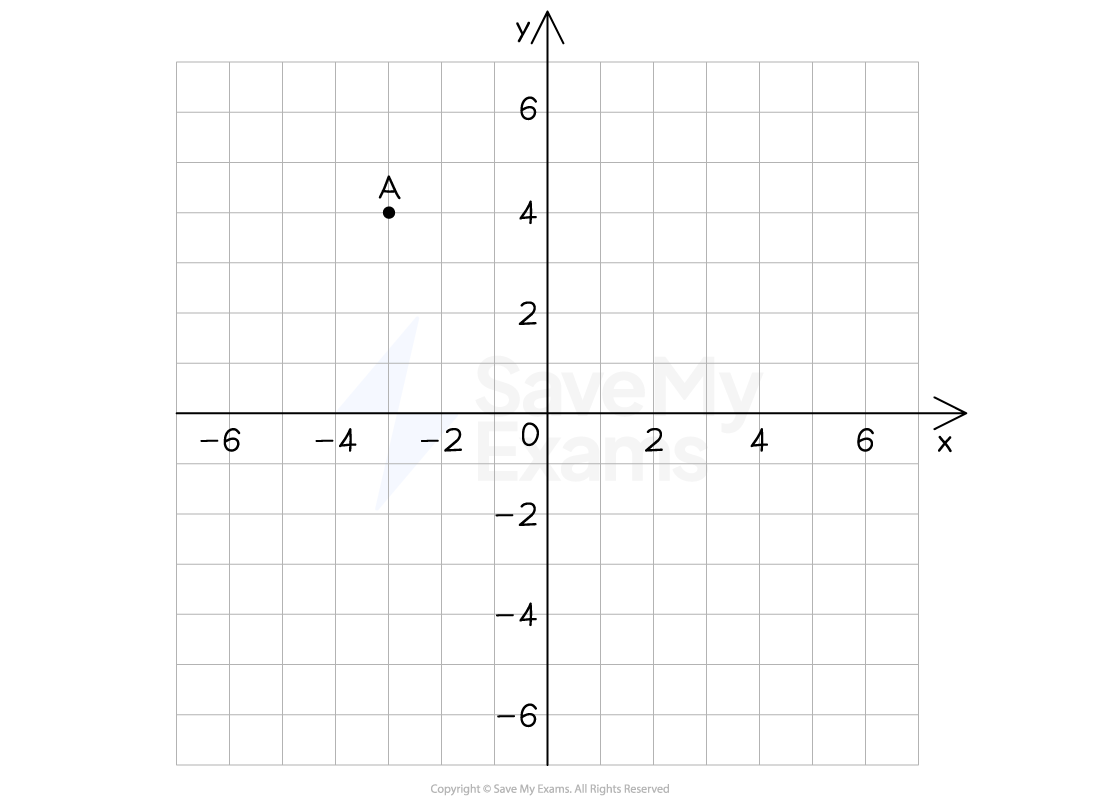
2d-coordinates-we 

A is 3 units to left, so x  is −3
A is 4 units up, so y  is 4
Give your answer in brackets
(−3, 4)

 

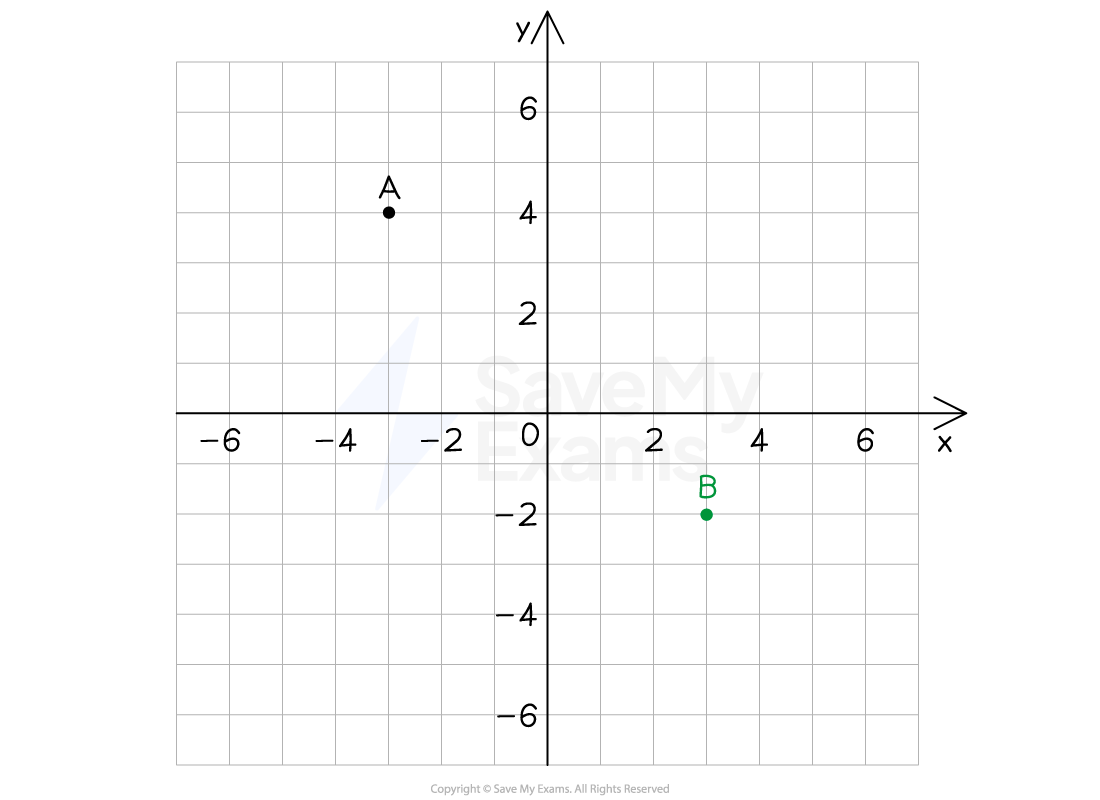
(b)
Mark the point B  with coordinates (-3, 2) on the same set of axes.
 
Start at the origin
Count 3 units right and two units down
Mark the point with a solid circle or cross and label it B
 
6j_PGh2e_2d-coordinates-we-answer

Gradient of a Line

What is the gradient of a line?

  • The gradient is a measure of how steep a straight line is
  • A gradient of 3 means:
    • For every 1 unit to the right, go up by 3
  • A gradient of -4 means:
    • For every 1 unit to the right, go down by 4 
  • A gradient of 3 is steeper than 2
    • A gradient of -5 is steeper than -4
  • A positive gradient means the line goes upwards (uphill)
    • Bottom left to top right 
  • A negative gradient means the line goes downwards (downhill)
    • Top left to bottom right

How do I find the gradient of a line?

  • Find two points on the line and draw a right-angled triangle
    • Then gradient space equals space fraction numerator change space in space y over denominator change space in space x end fraction
    • Or, in short, rise over run 
      • The rise is the vertical length of the triangle
      • The run is the horizontal length of the triangle
    • Put the correct sign on your answer
      • Positive for uphill lines
      • Negative for downhill lines
    • You can also find gradient of a line between two points, open parentheses x subscript 1 comma space y subscript 1 close parentheses and open parentheses x subscript 2 comma space y subscript 2 close parentheses 
      • Use the formula  fraction numerator y subscript 2 minus y subscript 1 over denominator x subscript 2 minus x subscript 1 end fraction

How do I draw a line with a given gradient?

  • To draw the gradient 2 over 3
    • The rise is 2
    • The run is 3
    • It is positive (uphill)
      • Move 3 units to the right and 2 units up
  • To draw the gradient negative 5 make it a fraction, negative 5 over 1
    • The rise is 5
    • The run is 1
    • It is negative (downhill)
      • Move 1 unit to the right and 5 units down

Examiner Tip

  • A lot of students forget to make their gradients negative for downhill lines!

Worked example

(a)

Find the gradient of the line shown in the diagram below.

screenshot-2023-02-12-at-20-42-17 

Find two points that the line passes through

open parentheses 0 comma space 2 close parentheses space and space open parentheses 1 comma space 5 close parentheses

Use the grid to draw a right-angled triangle
Find the 'rise' (vertical length) and 'run' (horizontal length)
 

cie-igcse-core-gradient-of-a-line-rn-we-a



Work out the fraction rise over run

3 over 1 equals 3

Look to see if the line is uphill or downhill

uphill, so the gradient is positive

The gradient is 3

 

(b)

On the grid below, draw the line with a gradient of −2 that passes through (0, 1).
 

Mark on the point (0, 1)
-2 is the fraction negative 2 over 1
The rise is 2, the run is 1, the line goes downhill (so 1 across, 2 down)

cie-igcse-gradients-of-lines-we-1

 

(c)begin mathsize 11px style table row blank row blank row blank end table end style

On the grid below, draw the line with a gradient of 2 over 3 that passes through (0,-1).
 

Mark on the point (0,-1) 
The rise is 2, the run is 3, the line goes uphill (so 3 across, 2 up)

cie-igcse-gradients-of-lines-we-2

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfNext topic

    Did this page help you?

    Mark

    Author: Mark

    Expertise: Maths

    Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.