Syllabus Edition

First teaching 2023

First exams 2025

Using Graphs (CIE IGCSE Maths: Core)

Revision Note

Test yourself

Author

Mark

Last updated

7 May 2024

Drawing Graphs Using a Table

How do I draw a graph using a table of values?

To create a table of values
- substitute different x-values into the equation
- This gives the y-values
To plot the points
- Use the x and y-values to mark crosses on the grid at the coordinates (x , y )
- Each point is expected to be plotted to an accuracy within half of the smallest square on the grid
Draw a single smooth freehand curve
- Go through all the plotted points
- Make it the shape you would expect
  - For example, quadratic curves have a vertical line of symmetry
- Do not use a ruler for curves!

Which numbers should I be careful with?

For quadratic graphs, be careful substituting in negative numbers
Always put brackets around them and use BIDMAS
- For example, x = -3 in y = -x² + 8x
  - becomes y = -(-3)² + 8(-3)
  - which simplifies to -9 - 24
  - so y = - 33
For reciprocal graphs like , do not include x = 0
- You cannot divide by zero
  - You get an error on your calculator
- There is no value at x = 0
  - The L-shaped branches can't cross the y-axis
- An example is given below with $y = \frac{1}{x}$

$x$	-3	-2	-1	0	1	2	3
$y$	$- \frac{1}{3}$	$- \frac{1}{2}$	$- 1$	No value	$1$	$\frac{1}{2}$	$\frac{1}{3}$

How do I use the table function on my calculator?

Calculators can create tables of values for you
Find the table function
- Type in the graph equation (called the function, f(x))
  - Use the alpha button then X or x
  - Press = when finished
- If you are asked for another function, g(x), press = to ignore it
Enter the start value
- The first x-value in the table
- Press =
Enter the end value
- The last x-value in the table
Enter the step size
- How big the steps (gaps) are from one x-value to the next
- Press =
Then scroll up and down to see all the y-values

Examiner Tip

If you find a point that doesn't seem to fit the shape of the curve, check your working!
If any y-values are given in the question, check that your calculations agrees with them.

Worked example

(a)

Complete the table of values for the graph of

y = 10 - 8 x^{2}

$x$	$- 1.5$	$- 1$	$- 0.5$	$0$	$0.5$	$1$	$1.5$
$y$		$2$					$- 8$

Use the table function on your calculator for

f (x) = 10 - 8 x^{2}

Start at -1.5, end at 1.5 and use steps of 0.5
On a non-calculator paper, substitute the x-values into the equation, for example x = -1.5

\begin{array}{rcl} y & = & 10 - 8 {(- 1.5)}^{2} \\ = & 10 - 8 \times 2.25 \\ = & 10 - 18 \\ = & - 8 \end{array}

$x$	$- 1.5$	$- 1$	$- 0.5$	$0$	$0.5$	$1$	$1.5$
$y$	-8	$2$	8	10	8	2	$- 8$

(b)

Plot the graph of

y = 10 - 8 x^{2}

on the axes below, for values of

x

from

- 1.5

1.5

Carefully plot the points from your table on to the grid
Note the different scales on the axes

Join the points with a smooth curve (do not use a ruler)

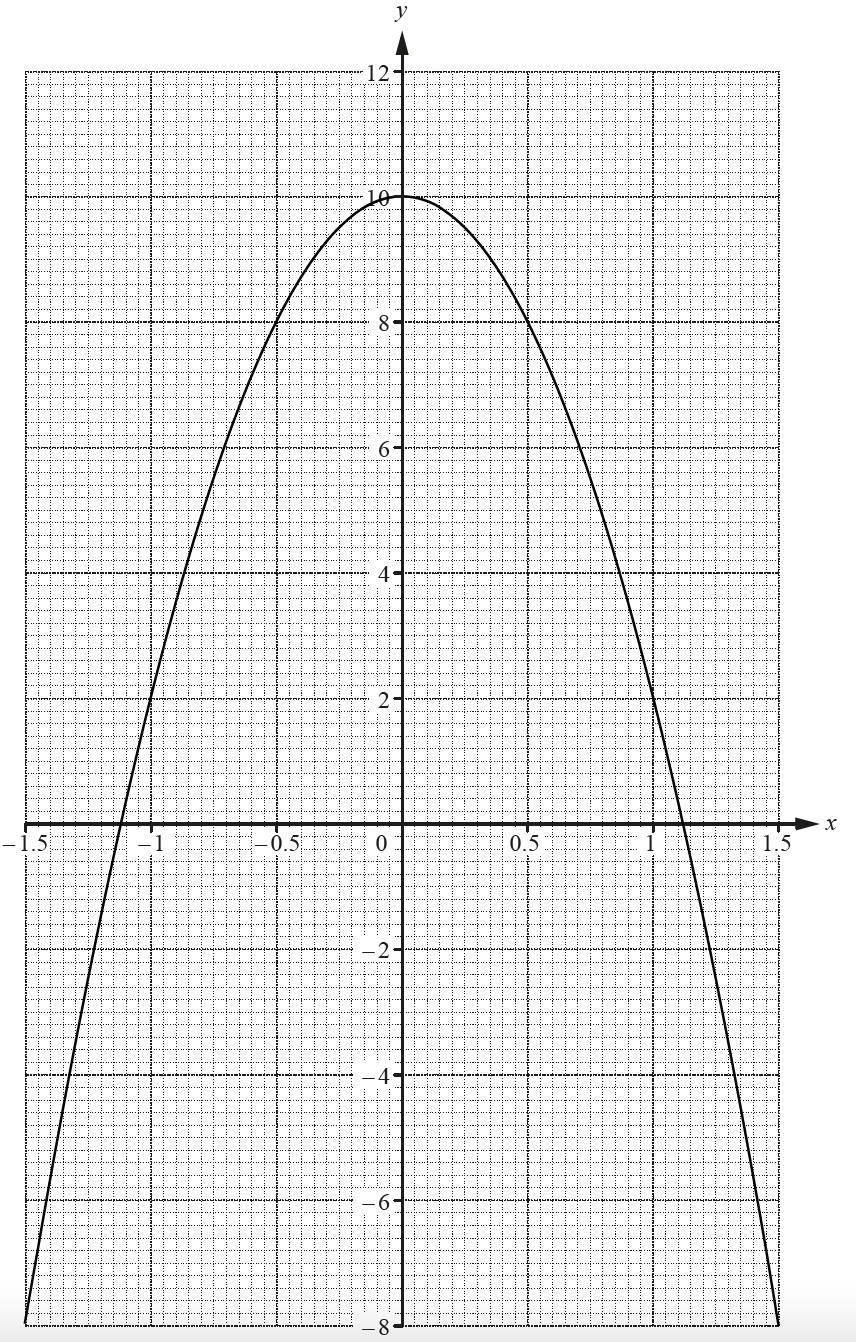
cie-igcse-2018-may-jun-1-7

(c)

Write down the equation of the line of symmetry of the curve.

There is a vertical line of symmetry about the y-axis

The equation of the y-axis is x = 0

x = 0

Solving Equations Using Graphs

How do I find the coordinates of points of intersection?

Plot two graphs on the same set of axes
- The points of intersection are where the two lines meet
For example, plot y = x² + 3x + 1 and y = 2x + 1 on the same axes
- They meet twice, as shown
- The coordinates of intersection are (-1, -1) and (0, 1)

Points of intersection between a curve and a line

How do I solve simultaneous equations graphically?

The x and y solutions to simultaneous equations are the x and y coordinates of the point of intersection
For example, to solve 2x - y = 3 and 3x + y = 7 simultaneously
- Rearrange them into the form y = mx + c
  - y = 2x - 3 and y = -3x + 7
- Use a table of values to plot each line
- Find the point of intersection, (2, 1)
- The solutions are therefore x = 2 and y = 1

Solving simultaneous equations graphically

How do I use graphs to solve equations?

This is easiest explained through an example
You can use the graph of $y = x^{2} - 4 x - 2$ to solve the following equations
- $x^{2} - 4 x - 2 = 0$
  - The solutions are the two x-intercepts
  - Where the curve cuts the x-axis (also called roots)
- - The solutions are the two x-coordinates where the curve intersects the horizontal line $y = 5$
- $x^{2} - 4 x - 2 = x + 1$ ,
  - the solutions are the two x-coordinates where the curve intersects the straight line $y = x + 1$
  - The straight line must be plotted on the same axes first
To solve a different equation like $x^{2} - 4 x + 3 = 1$
- add / subtract terms to both sides to get "graph = ..."
  - For example, subtract 5 from both sides
    - $x^{2} - 4 x - 2 = - 4$
    - This can now be done as above

Examiner Tip

When solving equations in x, only give x-coordinates as final answers
- Include the y-coordinates if solving simultaneous equations

Worked example

Use the graph of $y = 10 - 8 x^{2}$ shown to estimate the solutions of each equation given below.

The graph of y equals ten minus eight x squared

(a)

10 - 8 x^{2} = 0

This equals zero, so the x-intercepts are the solutions
Read off the values where the curve cuts the x-axis
Use a suitable level of accuracy (no more than 2 decimal places from the scale of this graph)

-1.12 and 1.12

These are the two solutions to the equation

x = -1.12 and x = 1.12

A range of solutions are accepted, such as "between 1.1 and 1.2"
Solutions must be ± of each other (due to the symmetry of quadratics)

(b)

10 - 8 x^{2} = 8

This equals 8, so draw the horizontal line y = 8
Find the x-coordinates where this cuts the graph

-0.5 and 0.5

These are the two solutions to the original equation

x = -0.5 and x = 0.5

The solutions here are exact

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves: