Probability Tree Diagrams (Cambridge (CIE) IGCSE Maths): Revision Note
Exam code: 0580 & 0980
Tree diagrams
How do I draw a tree diagram?
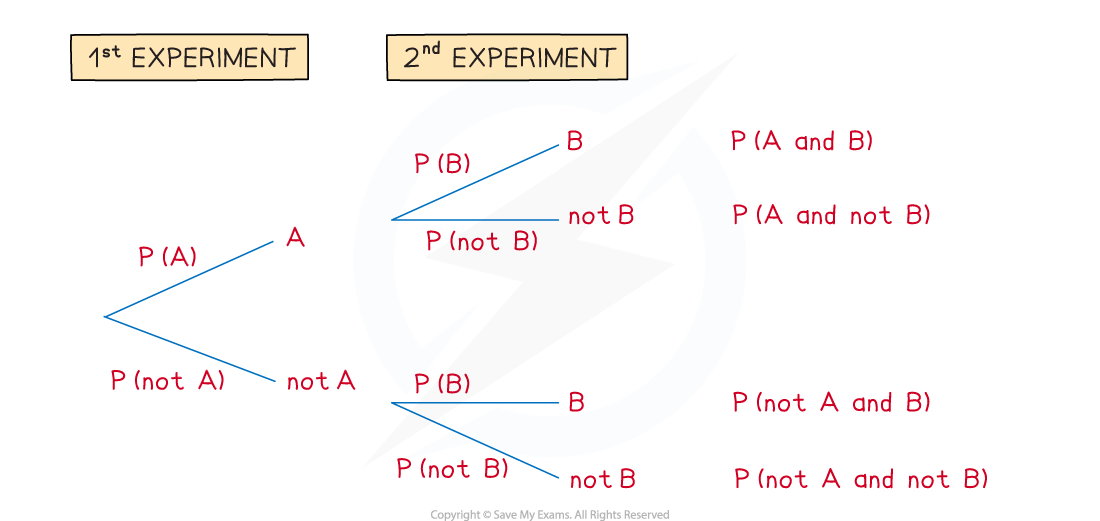
Tree diagrams can be used for repeated experiments with two outcomes
The 1st experiment has outcome A or not A
The 2nd experiment has outcome B or not B
Read the tree diagram from left to right along its branches
For example, the top branches give A followed by B
This is called A and B
How do I find probabilities from tree diagrams?
Write the probabilities on each branch
Remember that P(not A) = 1 - P(A)
Probabilities on each pair of branches add to 1
Multiply along the branches from left to right
This gives P(1st outcome and 2nd outcome)
Add between the separate cases
For example
P(AA or BB) = P(AA) + P(BB)
The probabilities of all possible cases add to 1
If asked to find the probability of at least one outcome, it is quicker to do 1 - P(none)
Examiner Tips and Tricks
When multiplying along branches with fractions, don't cancel fractions in your working - having the same denominator makes them easier to add together!
Worked Example
A worker drives through two sets of traffic lights on their way to work.
Each set of traffic lights has only two options: green or red.
The probability of the first set of traffic lights being on green is .
The probability of the second set of traffic lights being on green is .
(a) Draw and label a tree diagram. Show the probabilities of every possible outcome.
Answer:
Work out the probabilities of each set of traffic lights being on red, R
Use P(red) = 1 - P(green)
Draw the branches (with a label of G or R on the ends)
Write the probabilities above each branch
Calculate probabilities of each outcome by multiplying along the branches from left to right
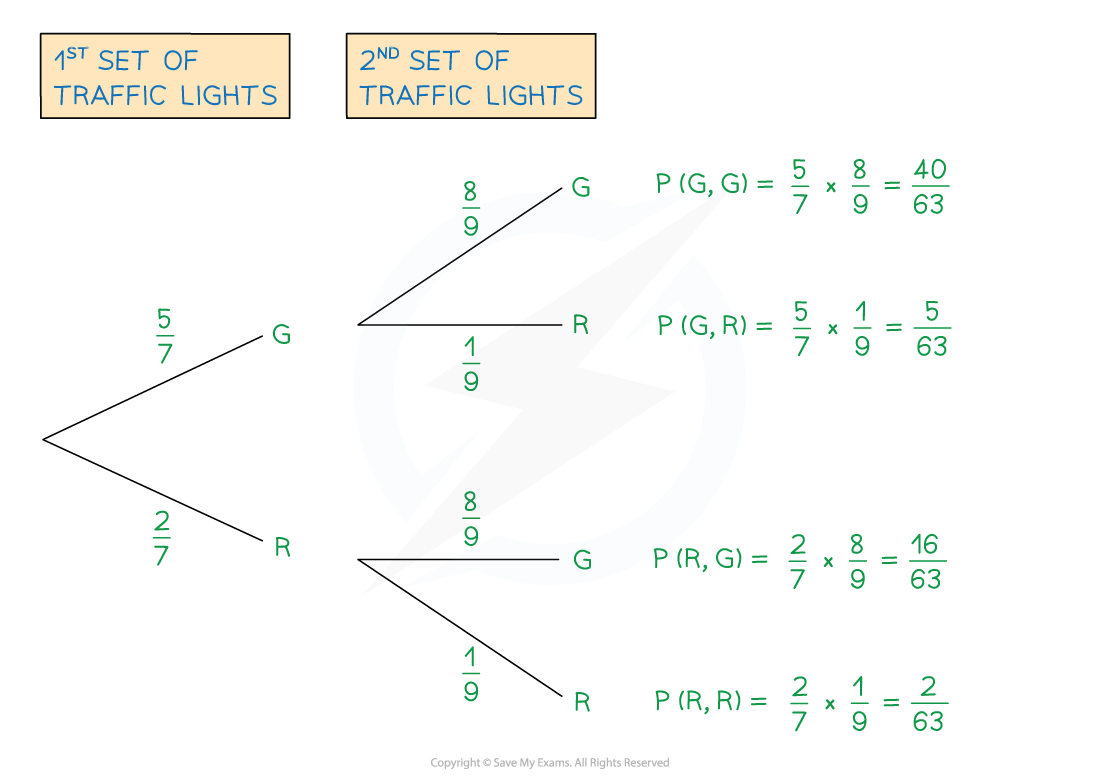
(b) Find the probability that both sets of traffic lights are on red.
Answer:
This is the answer for P(R, R) from the tree diagram
(c) Find the probability that at least one set of traffic lights are on red.
Answer:
This means the 1st is green and the 2nd is red
Or the 1st is red and the 2nd is green
Or the 1st is red and the 2nd is red ('at least one' could mean both)
Add between the separate cases
Alternative Method
At least one red means all the possible cases shown except two greens
So P(at least 1 red) = 1 - P(two greens)

Unlock more, it's free!
Did this page help you?