IGCSEMathsEdexcelMaths AHigherRevision NotesSequences, Functions & GraphsTransformations of GraphsStretches of Graphs

Stretches of Graphs (Edexcel IGCSE Maths A): Revision Note

Mark Curtis

Written by: Mark Curtis

Reviewed by: Dan Finlay

Updated on

Edexcel Maths A: HigherEdexcel Maths A (Modular): Higher Unit 2

Did this video help you?

Stretches of Graphs

What are stretches of graphs?

  • Stretches of graphs are a type of transformation that pushes points away from, or towards, the x-axis or y-axis

    • Graphs look like they have been stretched or squashed

      • either horizontally or vertically

A graph being stretched vertically (on the left) or horizontally (on the right).
A graph being stretched vertically (left) or horizontally (right)

How do I stretch graphs?

  • Let y equals straight f open parentheses x close parentheses be the equation of the original graph

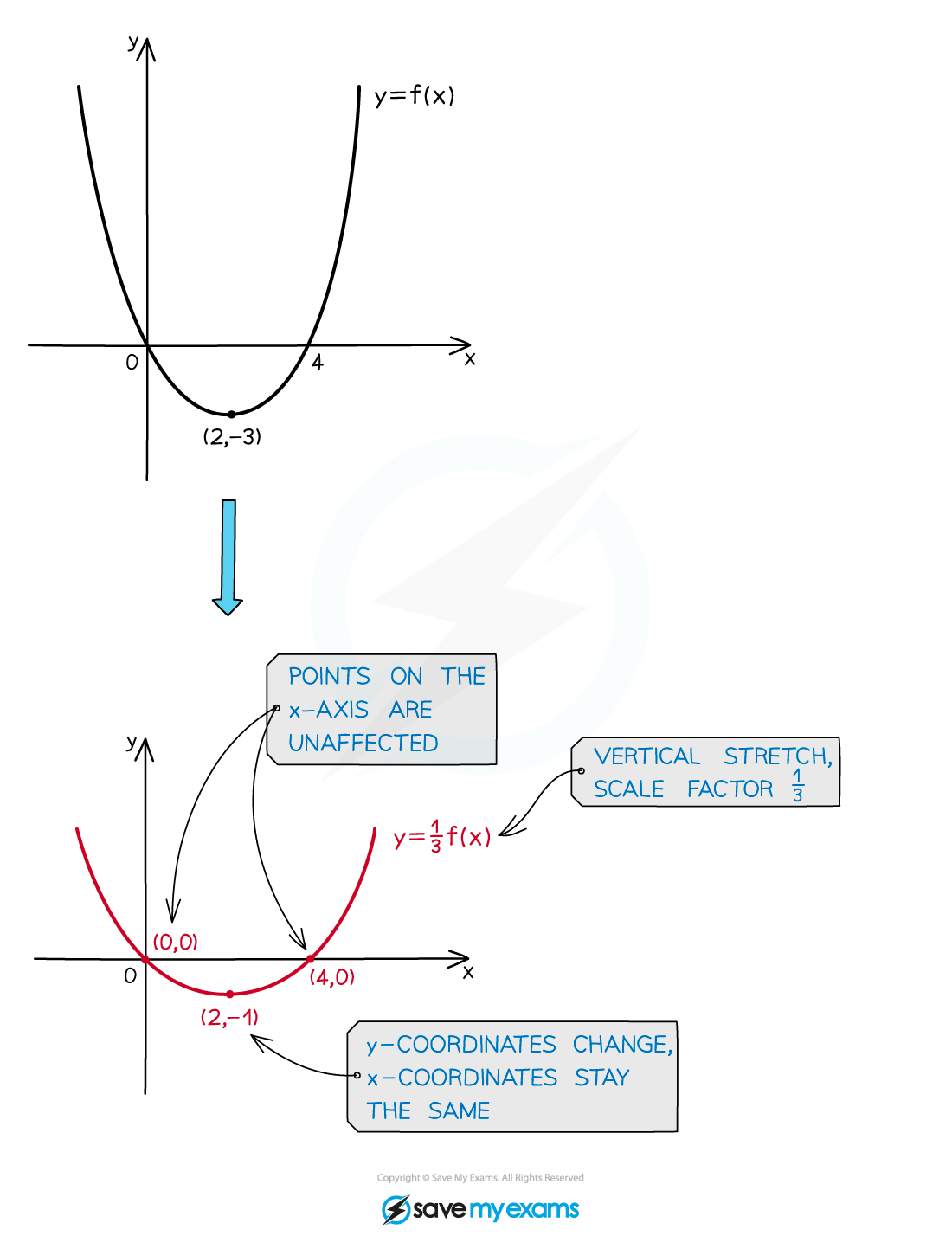
Vertical stretches: y=af(x)

  • y equals a straight f open parentheses x close parentheses is a vertical stretch (in the y-direction) of scale factor a

    • The x-coordinates stay the same but the y coordinates are multiplied by a

    • Points appear to move parallel to the y-axis

      • either stretching vertically away from the x-axis if a greater than 1

      • or squashing vertically towards the x-axis if 0 less than a less than 1

    • Points on the x-axis stay where they are

Graph showing the function y = f(x) and its transformation y = (1/3)f(x), indicating vertical stretch by a factor of 1/3. Points (2, -3) and (2, -1) shown.

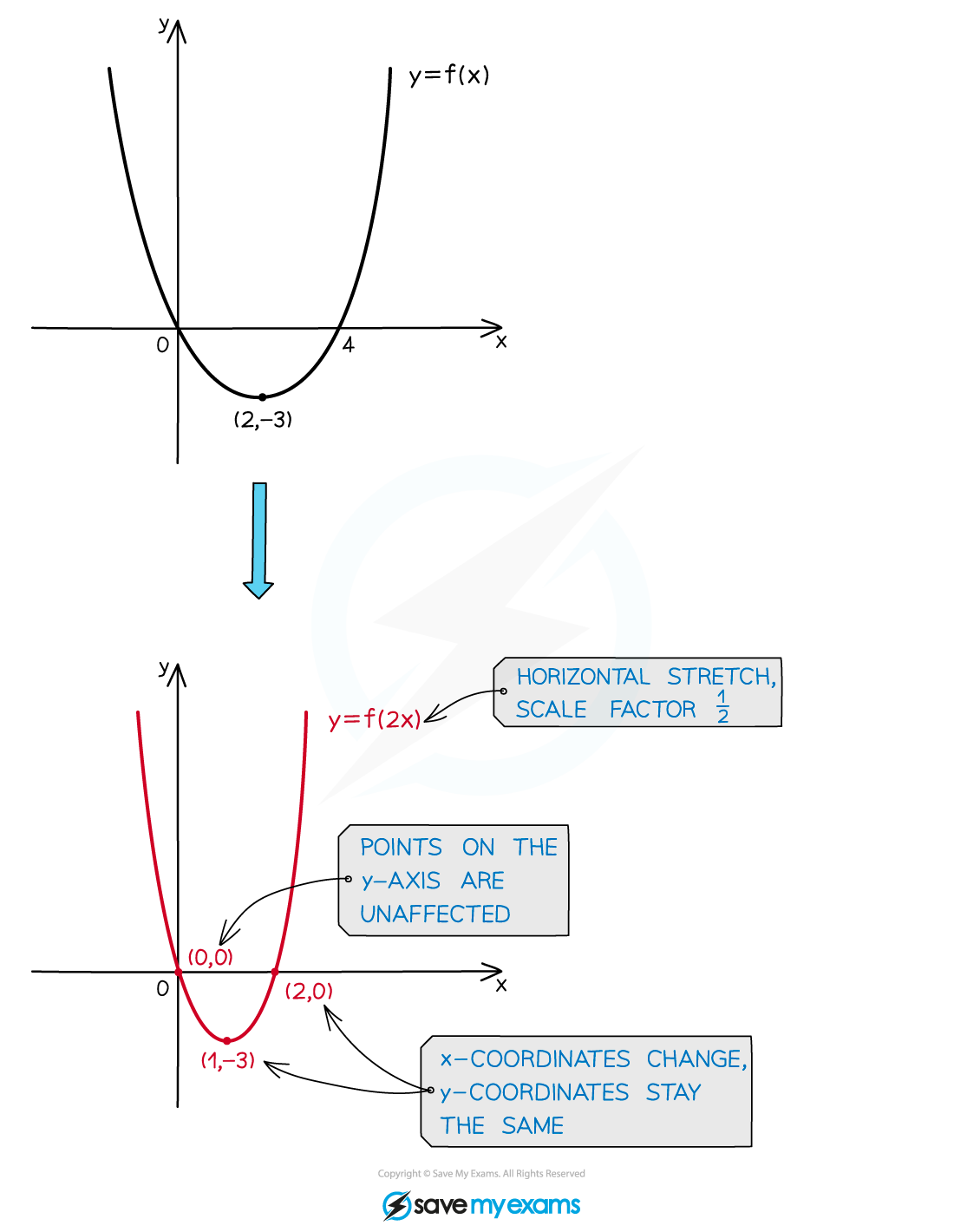
Horizontal stretches: y=fa(x)

  • y equals straight f open parentheses a x close parentheses is a horizontal stretch (in the y-direction) of scale factor 1 over a (not a)

    • The y-coordinates stay the same but the x coordinates are multiplied by 1 over a (divided by a)

    • Points appear to move parallel to the x-axis

      • either squashing horizontally towards the y-axis if a greater than 1

      • or stretching horizontally away from the y-axis if 0 less than a less than 1

    • Points on the y-axis stay where they are

  • This means y equals straight f open parentheses 2 x close parentheses is more like a horizontal squash of scale factor 2

    • though the correct way to say this is a horizontal stretch of scale factor 1 half

      • This also means that straight f open parentheses x over 2 close parentheses is a horizontal stretch of scale factor 2

Stretching a graph horizontally by scale factor one half. y-coordinates stay in same place, x-coordinates change

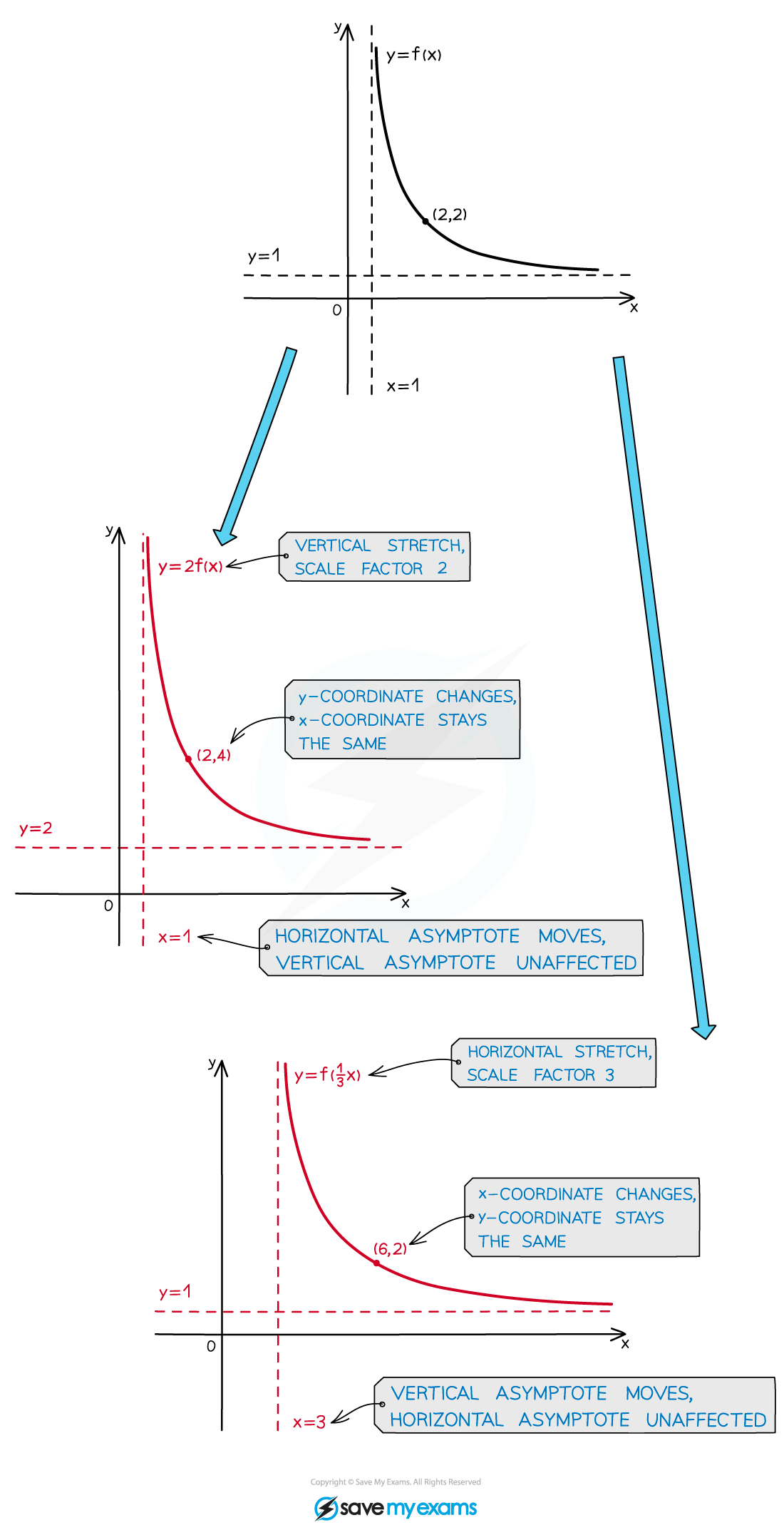
What happens to asymptotes when a graph is stretched?

  • Any asymptotes of straight f open parentheses x close parentheses are also stretched

A diagram shows transformations of the function y = f(x). It illustrates vertical and horizontal stretches, their effects on asymptotes, and coordinate changes.

How does a stretch affect the equation of the graph?

  • When a graph is stretched, you can change its equation algebraically

    • There is no need to sketch the graph

  • Stretching vertically by a scale factor of 3 puts a 3 in front of the whole equation

    • For example, y equals x squared plus 2 x becomes y equals 3 open parentheses x squared plus 2 x close parentheses

      • This simplifies to y equals 3 x squared plus 6 x

  • Stretching horizontally by a scale factor of 1 third ("squashing horizontally" by a scale factor of 3) replaces any x with open parentheses 3 x close parentheses in the equation

    • For example, y equals x squared plus 2 x becomes y equals open parentheses 3 x close parentheses squared plus 2 open parentheses 3 x close parentheses

      • This simplifies to y equals 9 x squared plus 6 x

How do I apply a combined stretch?

  • The graph of y equals b straight f open parentheses a x close parentheses is a combined stretch, both horizontally and vertically

    • It does not matter which order you apply these in

      • For example, a horizontal stretch of scale factor 1 over a followed by a vertical stretch of scale factor b

Worked Example

The diagram below shows the graph of y equals straight f open parentheses x close parentheses.

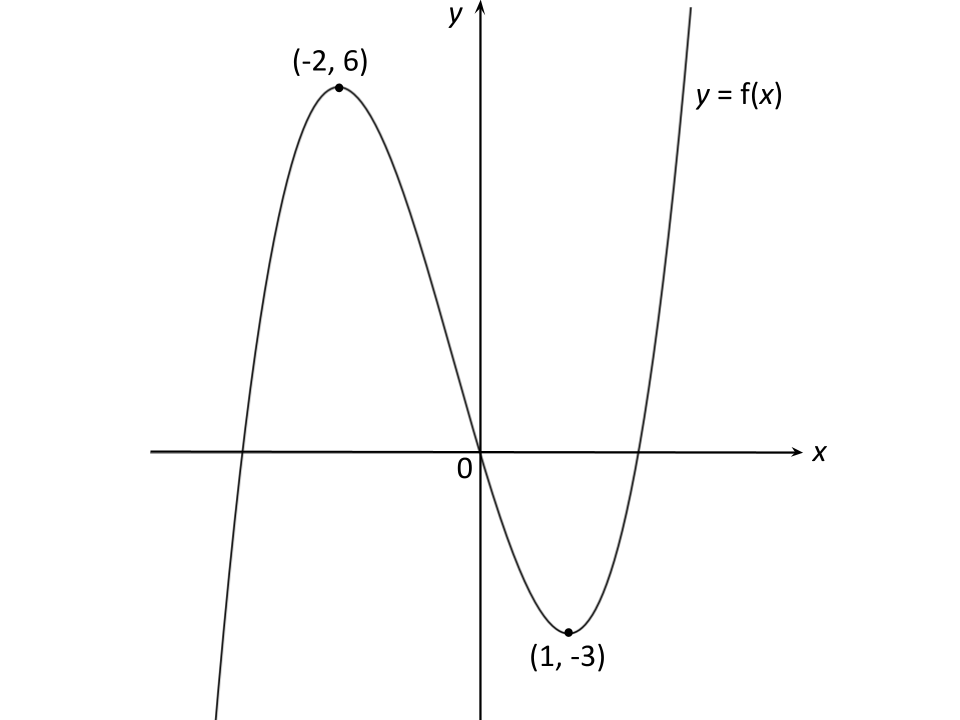
A positive cubic graph f(x)

Sketch the graph of y equals 2 straight f open parentheses x over 3 close parentheses.

straight f open parentheses x over 3 close parentheses represents a horizontal stretch of scale factor fraction numerator 1 over denominator open parentheses 1 third close parentheses end fraction equals 3
And 2 straight f open parentheses... close parentheses represents a vertical stretch of scale factor 2

Apply these in any order, e.g. start with the horizontal stretch, scale factor 3

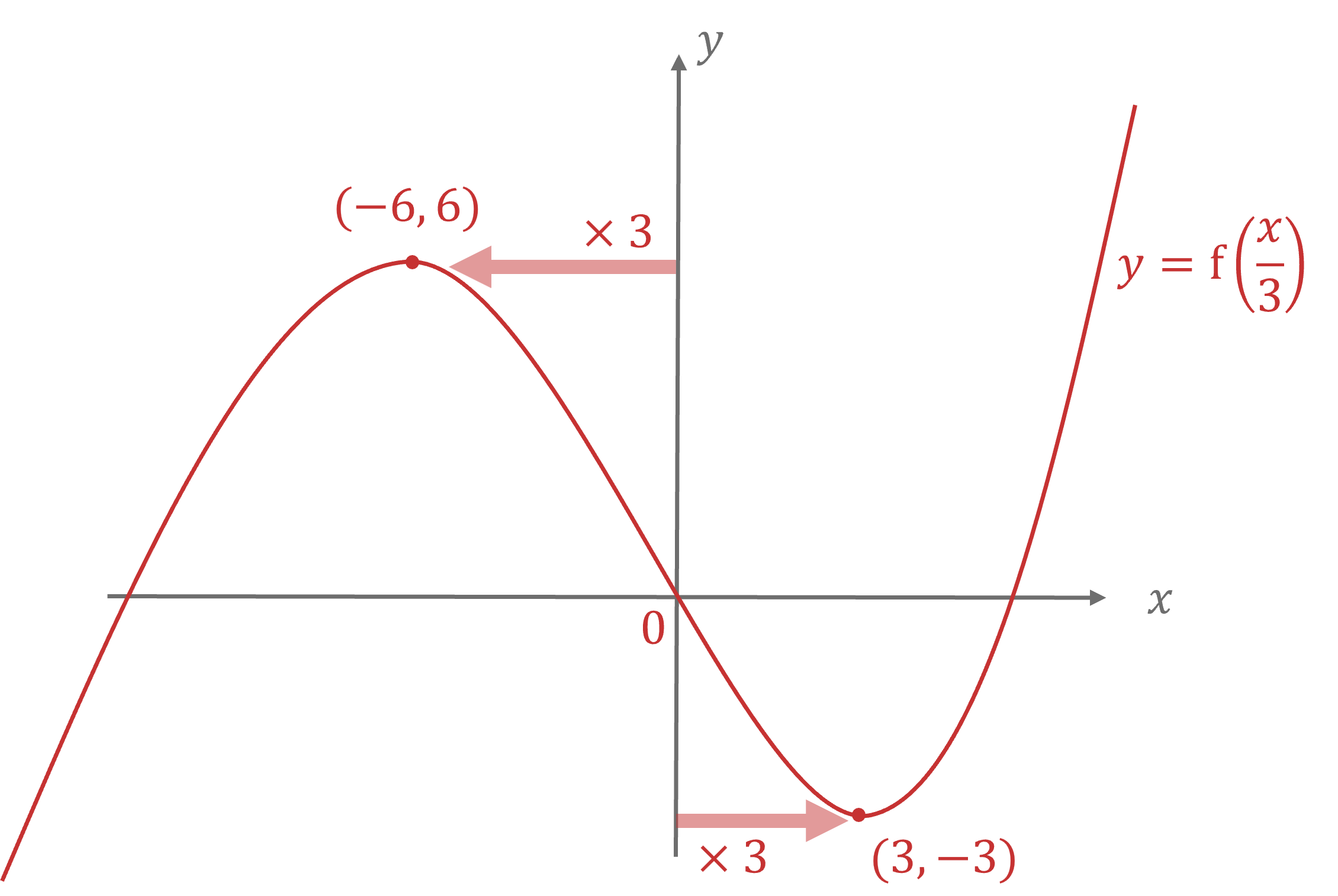
Graph of the function y = f(x/3) with key points labeled (-6, 6) and (3, -3).

Now apply a vertical stretch of scale factor 2

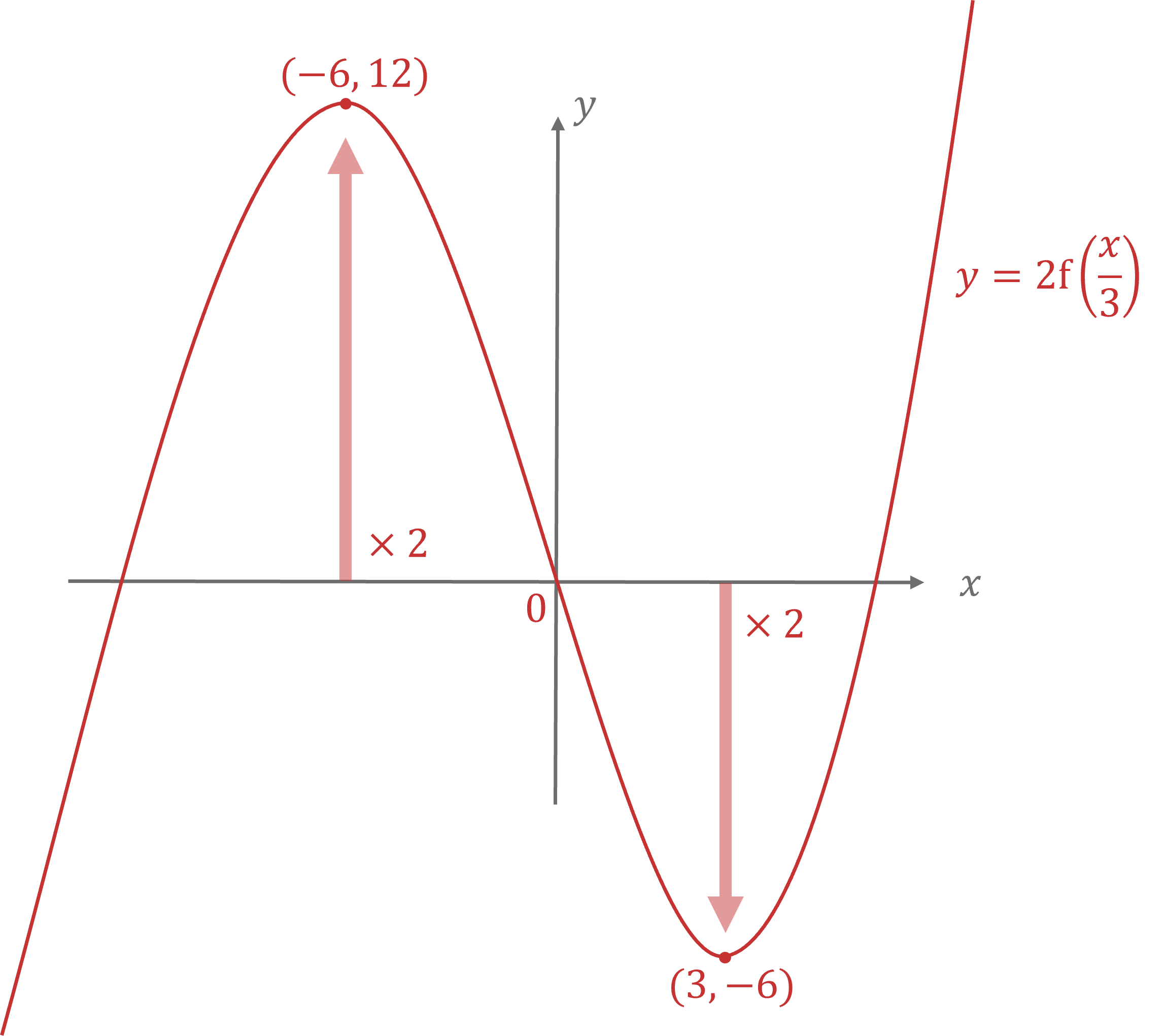
Graph of the function y=2f(x/3) showing a curve with marked points at (-6,12) and (3,-6) and vertical stretches by a factor of 2 along y-axis.

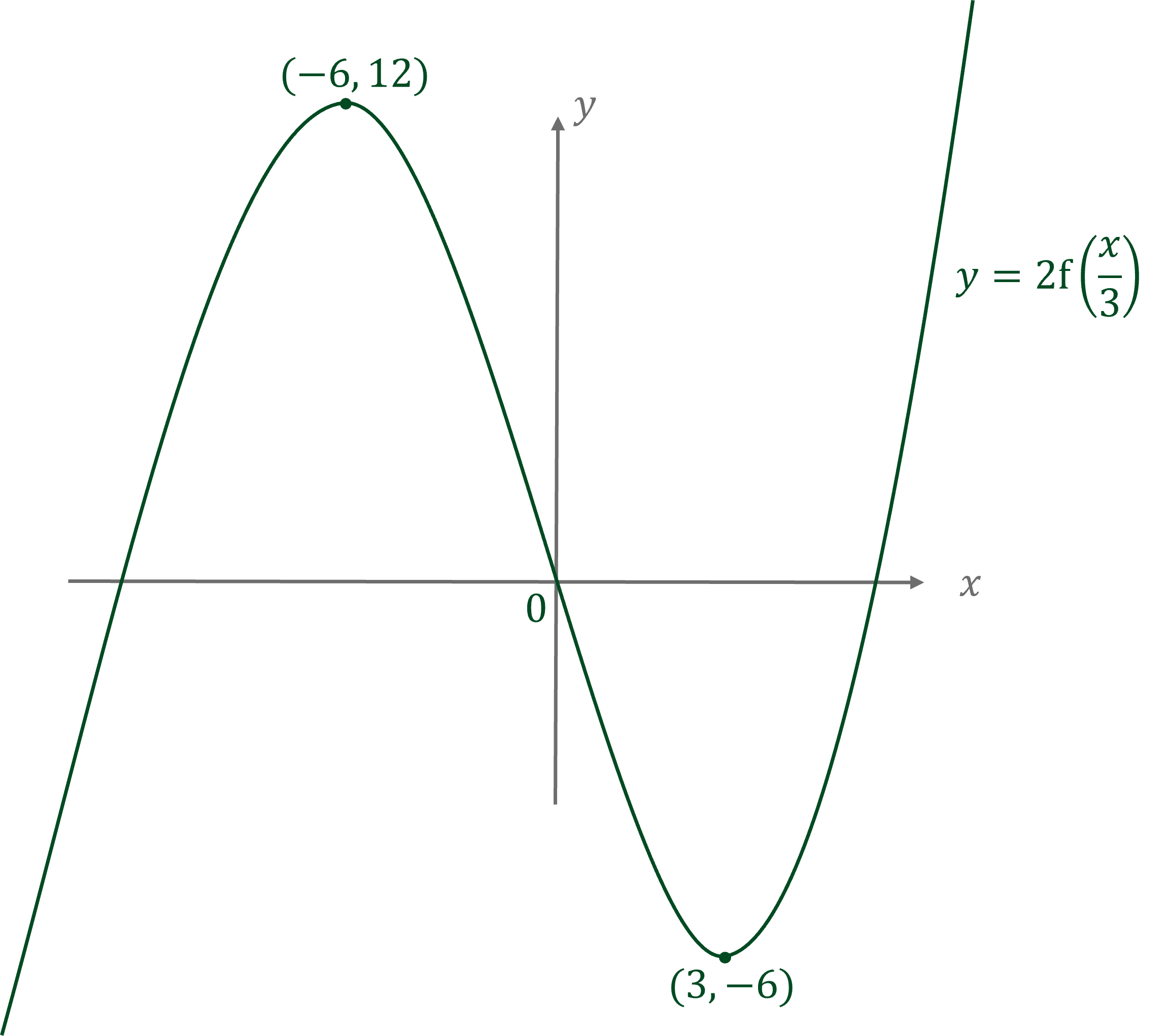
Show the coordinates of the new points clearly

Graph of the function y = 2f(x/3) with a peak at (-6,12) and a trough at (3,-6), crossing the y-axis at 0. Axes labelled x and y.
👀 You've read 1 of your 5 free revision notes this week
An illustration of students holding their exam resultsUnlock more revision notes. It's free!

By signing up you agree to our Terms and Privacy Policy.

Already have an account? Log in

Test yourselfFlashcards

Did this page help you?

Previous:Reflections of GraphsNext:Differentiation
Author
Reviewer
Mark Curtis

Author: Mark Curtis

Expertise: Maths Content Creator

Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.

Dan Finlay

Reviewer: Dan Finlay

Expertise: Maths Subject Lead

Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

Download notes on Stretches of Graphs