HCF & LCM (Edexcel IGCSE Maths A (Modular)) : Revision Note
Did this video help you?
Highest Common Factor (HCF)
What is the highest common factor (HCF) of two numbers?
A common factor of two numbers is a value that both numbers can be divided by, leaving no remainder
1 is always a common factor of any two numbers
Any factor of a common factor will also be a common factor of the original two numbers
6 is a common factor of 24 and 30
Therefore 1, 2 and 3 are also common factors of 24 and 30
The highest common factor is the largest common factor of the two numbers
The highest common factor is useful when simplifying fractions or factorising expressions
How do I find the highest common factor (HCF) of two numbers?
To find common factors:
write out the factors of each number in a list
identify the numbers that appear in both lists
The highest common factor will be the largest factor that appears in both lists
How can I use a Venn diagram to find the highest common factor (HCF) of two numbers?
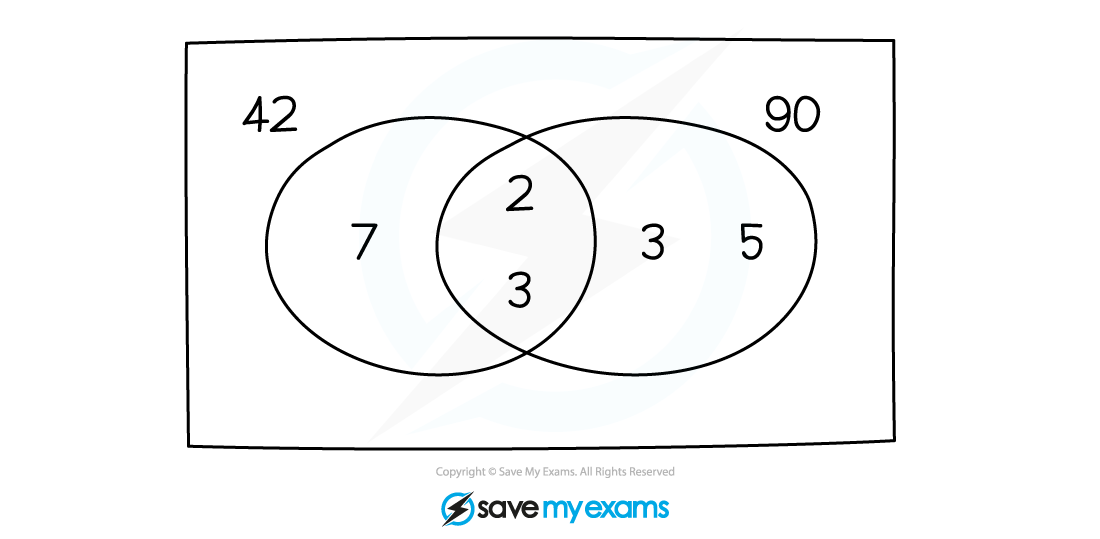
Write each number as a product of its prime factors
42 = 2×3×7 and 90 = 2×3×3×5
Find the prime factors that are common to both numbers and put these in the centre of the Venn diagram
42 and 90 both have a prime factor of 2
Put 2 in the centre of the diagram
Although 3 appears twice in the prime factors of 90, it appears once in the prime factors of 42
Put a single 3 in the centre of the diagram
If there are no common prime factors, put a 1 in the centre of the diagram
Put the remaining prime factors in the respective regions
7 would go in the region for 42
3 and 5 would go in the region for 90
The highest common factor is the product of the numbers in the centre
The HCF of 42 and 90 is 2×3, which is 6
If there are no common prime factors then the HCF is 1
How can I use the powers of prime factors to find the highest common factor (HCF) of two numbers?
Write each number as a product of the powers of its prime factors
24 = 23×3 and 60 = 22×3×5
Find all common prime factors and identify the highest power that appears in both numbers
The highest power of 2 in both is 22
22 is a common factor
The highest power of 3 in both is 31
3 is a common factor
No other prime number appears in both
The highest common factor is the product of the common powers of primes
The HCF of 24 and 60 is 22×3 which is 12
Examiner Tips and Tricks
The highest common factor of two numbers could be one of the numbers!
The highest common factor of 4 and 12 is 4
Worked Example
Find the highest common factor of 36 and 120.
Write both numbers as a product of prime factors
36 = 2×2×3×3 = 22 × 32
120 = 2×2×2×3×5 = 23 × 3 × 5
Write the prime factors in a Venn diagram
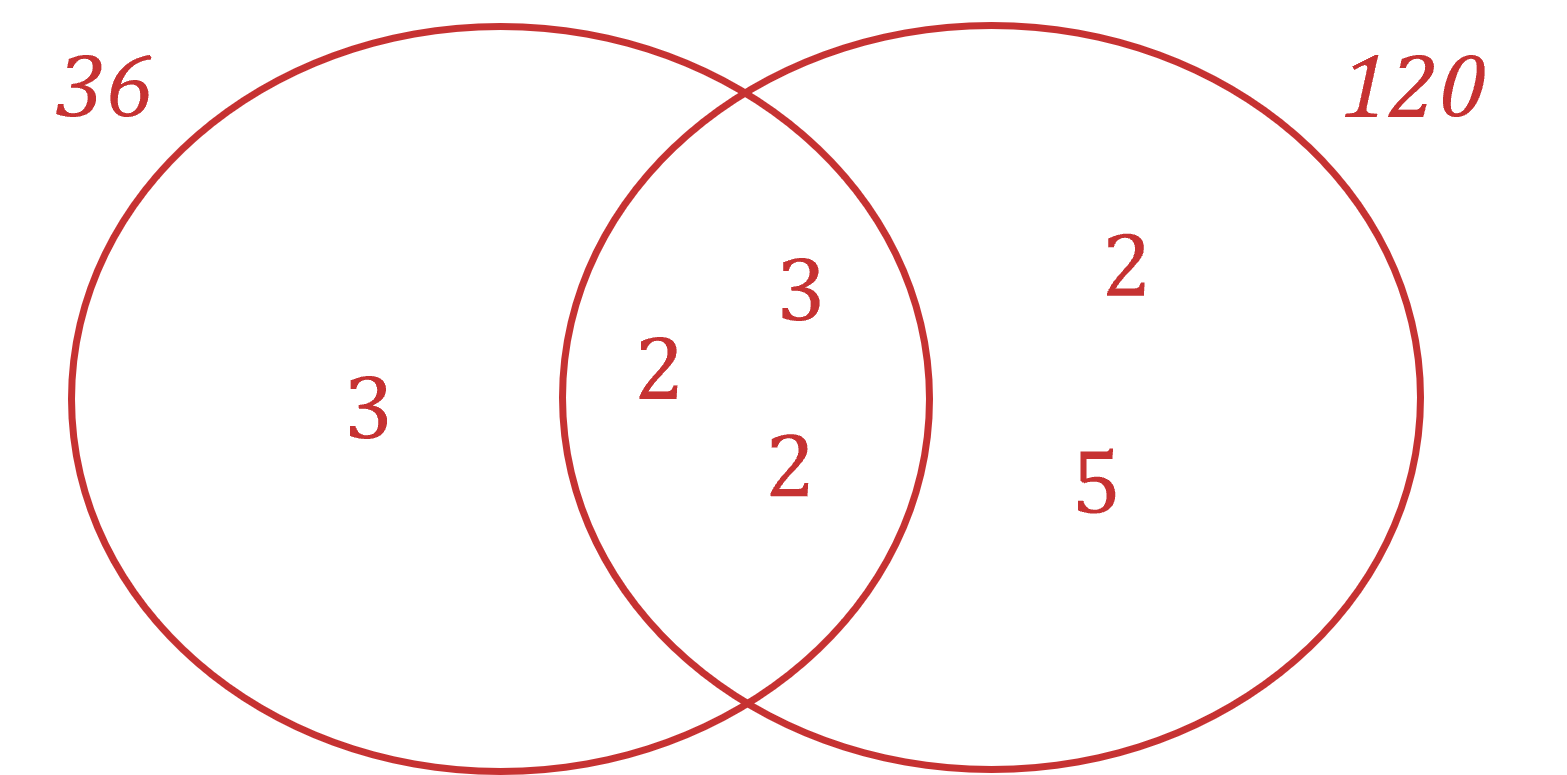
Multiply the common prime factors in the centre
HCF = 2 × 2 × 3
Alternatively, list the factors for each number
36: 1, 2, 3, 4, 6, 9, 12, 18, 36
120: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
Another alternative is to find the highest common powers of primes
22 and 31 are the highest common powers of primes
HCF = 22 × 31
HCF = 12
Lowest Common Multiple (LCM)
What is the lowest common multiple (LCM) of two numbers?
A common multiple of two numbers is a number that appears in both of their times tables
The product of the original two numbers is always a common multiple (but not necessarily the lowest)
Any multiple of a common multiple will also be a common multiple of the original two numbers
30 is a common multiple of 3 and 10
Therefore 60, 90, 120, ... are also common multiples of 3 and 10
The lowest common multiple is the smallest common multiple between two numbers
This is useful when finding a common denominator and when adding or subtracting fractions
How do I find the lowest common multiple (LCM) of two numbers?
To find the lowest common multiple of two numbers:
write out the first few multiples of each number
identify the multiples that appear in both lists
If there are none then write out the next few multiples of each number until you find a common multiple
The lowest common multiple will be the smallest multiple that appears in both lists
How can I use a Venn diagram to find the lowest common multiple (LCM) of two numbers?
Write each number as a product of its prime factors
42 = 2×3×7 and 90 = 2×3×3×5
Find the prime factors that are common to both numbers and put these in the centre of the Venn diagram
42 and 90 both have a prime factor of 2
Put a 2 in the centre of the diagram
Although 3 appears twice in the prime factors of 90, it appears once in the prime factors of 42
Put a single 3 in the centre of the diagram
If there are no common prime factors then put a 1 in the centre of the diagram
Put the remaining prime factors in the respective regions
7 would go in the region for 42
3 and 5 would go in the region for 90
The lowest common multiple is the product of all the numbers in the Venn diagram
The LCM of 42 and 90 is 7×2×3×3×5, which is 630

How can I use the powers of prime factors to find the lowest common multiple (LCM) of two numbers?
Write each number as a product of the powers of its prime factors
and
Find the highest power of each and every prime that appears in either number (they do not have to be common primes)
23 is the highest power of 2 shown (from 72)
33 is the highest power of 3 shown (from 540)
51 is the highest power of 5 shown (from 540)
Note: 5 is not a common prime in 72 and 540, but it is still needed for the LCM
The lowest common multiple is the product of these highest powers
The LCM of 72 and 540 is 23×33×5, which is 1080
Examiner Tips and Tricks
The lowest common multiple of two numbers could be one of the numbers!
The lowest common multiple of 4 and 12 is 12
Worked Example
Find the lowest common multiple of 36 and 120.
Write both numbers as a product of prime factors
36 = 2×2×3×3 = 22 × 32
120 = 2×2×2×3×5 = 23 × 3 × 5
Write the prime factors in a Venn diagram

Multiply all the prime factors in the diagram
LCM = 3 × 2 × 2 × 3 × 2 × 5
An alternative method is to write out the multiples
36: 26, 72, 108, 144, 180, 216, 252, 288, 324, 360, 396, ...
120: 120, 240, 360, 480, ...
Another alternative method is to find the highest powers of each and every prime that appear
Then multiply these together
23 × 32 × 51
LCM = 360

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

