Geometrical Proof (Edexcel IGCSE Maths A (Modular)): Revision Note
Exam code: 4XMAF/4XMAH
Geometrical proof
What is a geometrical proof?
Geometric proof involves using known rules about geometry to prove a new statement about geometry
A proof question might start with “Prove…” or “Show that …”
The rules that you might need to use to complete a proof include;
Properties of 2D shapes
Especially triangles and quadrilaterals
Basic angle properties
Angles in polygons
Angles in parallel lines
Congruence and similarity
Pythagoras theorem
You will need to be familiar with the vocabulary of the topics above, in order to fully answer many geometrical proof questions
How do I write a geometrical proof?
Usually you will need to write down two or three steps to prove the statement
At each step, you should write down a fact and a reason
For example, “AB = CD, opposite sides of a rectangle are equal length”
The proof is complete when you have written down all the steps clearly
Use the diagram!
Add key information such as angles or line lengths to the diagram as you work through the steps
but you must write them down in your written answer too
What geometric notation should I use?
Points or vertices of a shape are labelled with capital letters
A, B, C and D are the vertices of the quadrilateral
O is the centre of the circle
Two letters are used to represent the line between the points
AB is the line between points A and B
Three letters are used to represent the angle formed by the three points
Angle ABC is the angle between lines AB and BC
The letter in the middle is the point where the angle is at
Multiple letters are used to represent the whole shape
ABCD is a quadrilateral
The letters are written down so that they go clockwise around the shape
If you use a variable to represent a length or an angle then write it down
Angle ABC =

How can I prove that the exterior angle of a triangle is equal to the sum of the interior angles at the other two vertices?
Let a, b and c be the three interior angles in a triangle
Let d be the exterior angle next to the interior angle c
Split d into two angles by drawing a parallel line to the other side of the triangle
There will be an angle alternate to angle a
There will be an angle corresponding to angle b
Therefore the exterior angle is the sum of the two opposite interior angles

What are common geometric reasons I can use?
There are common phrases that are sufficient as explanations and should be learnt
These will be what mark schemes look for
For triangles and quadrilaterals
Angles in a triangle add up to 180°
Base angles of an isosceles triangle are equal
Angles in an equilateral triangle are equal
Angles in a quadrilateral add up to 360°
An exterior angle of a triangle is equal to the sum of the interior opposite angles
For straight lines
Vertically opposite angles are equal
Angles on a straight line add up to 180°
Angles at a point add up to 360°
For parallel lines
Alternate angles are equal
Corresponding angles are equal
Allied (or co-interior) angles add up to 180°
For polygons
Exterior angles of a polygon add up to 360°
The interior and exterior angle of any polygon add up to 180°
Examiner Tips and Tricks
DO show all the key steps. If in doubt, include it.
DON'T write in full sentences. For each step, just write down the fact, followed by the key mathematical reason that justifies it.
Worked Example
In the diagram below, AC and DG are parallel lines. B lies on AC, E and F lie on DG and triangle BEF is isosceles.
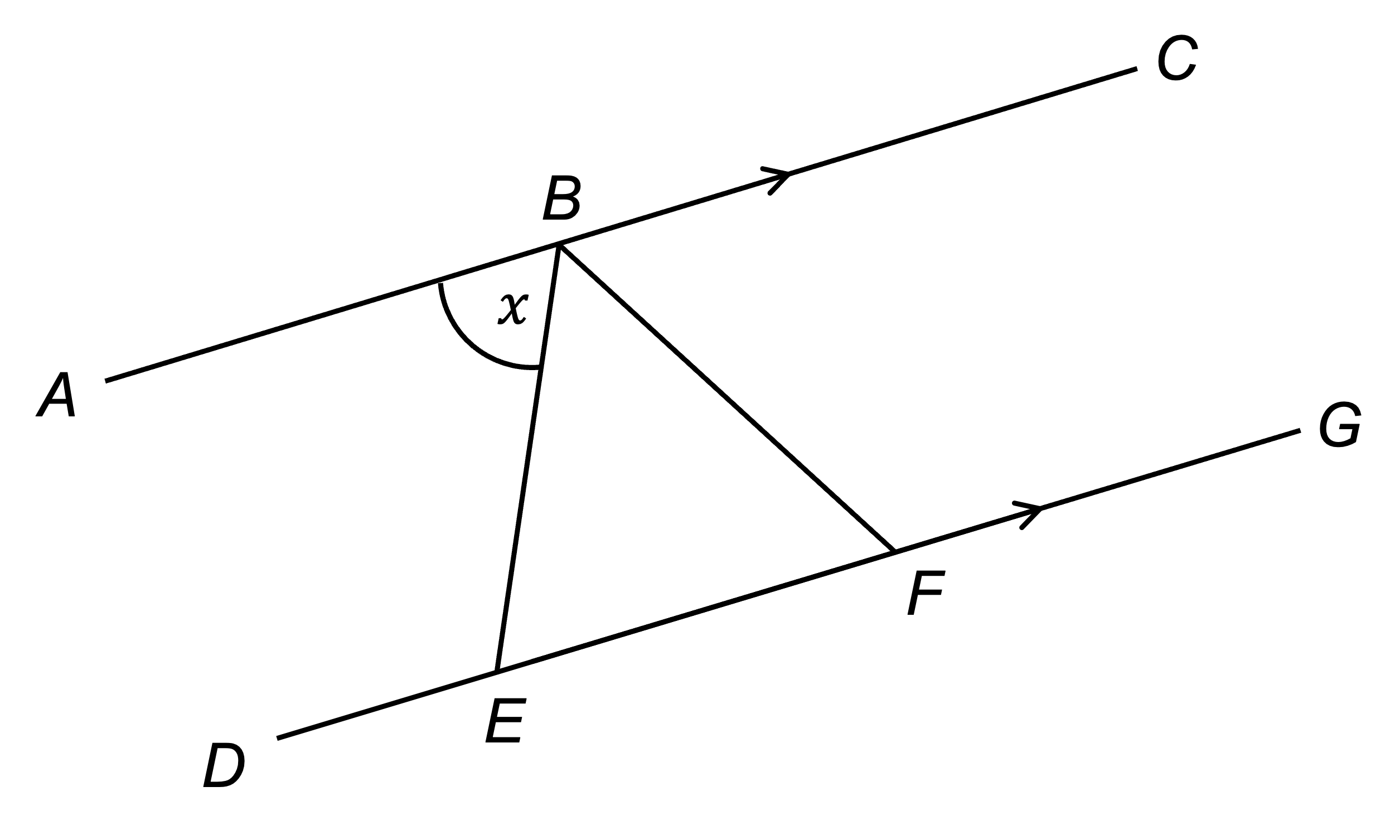
Prove that angle EBF is . Give reasons for each stage of your working.
Answer:
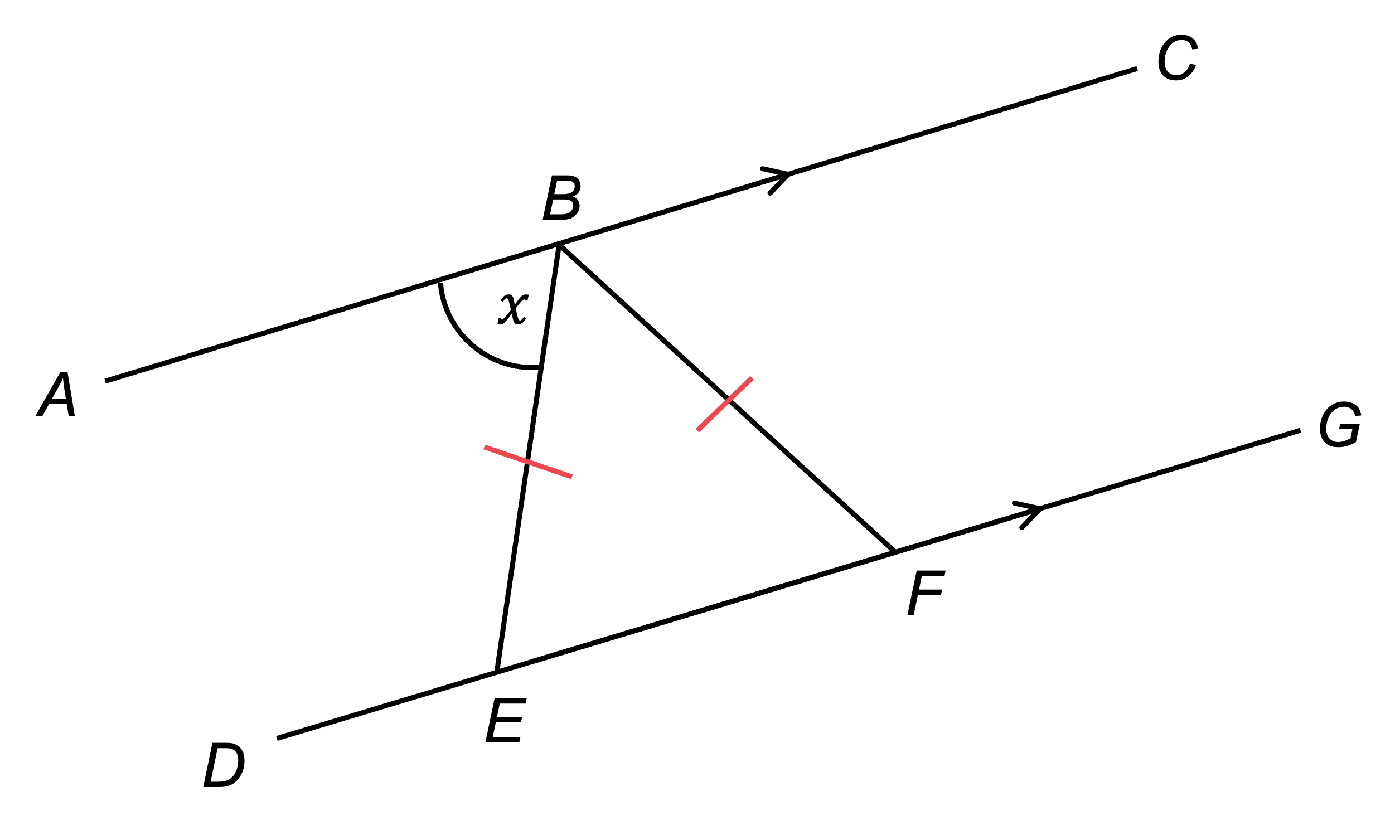
Mark on the diagram that triangle BEF is isosceles
AC and DG are parallel lines, so using alternate angles we know that angle BEF =
Mark this on the diagram
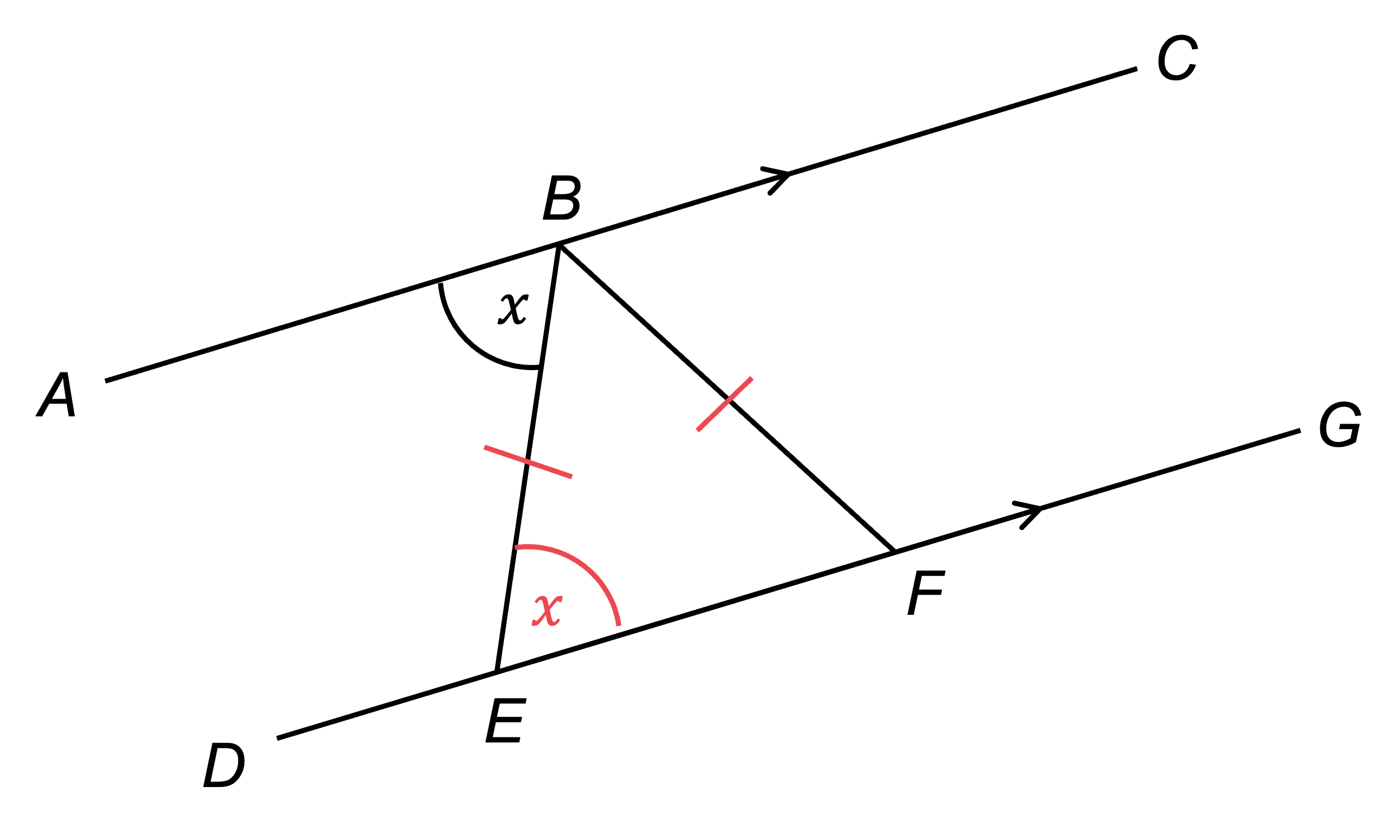
Write the fact, and the reason using the key mathematical vocabulary
angle BEF = , alternate angles are equal
Now using the fact that triangle BEF is isosceles, we can see that angle BFE =
Mark this on the diagram
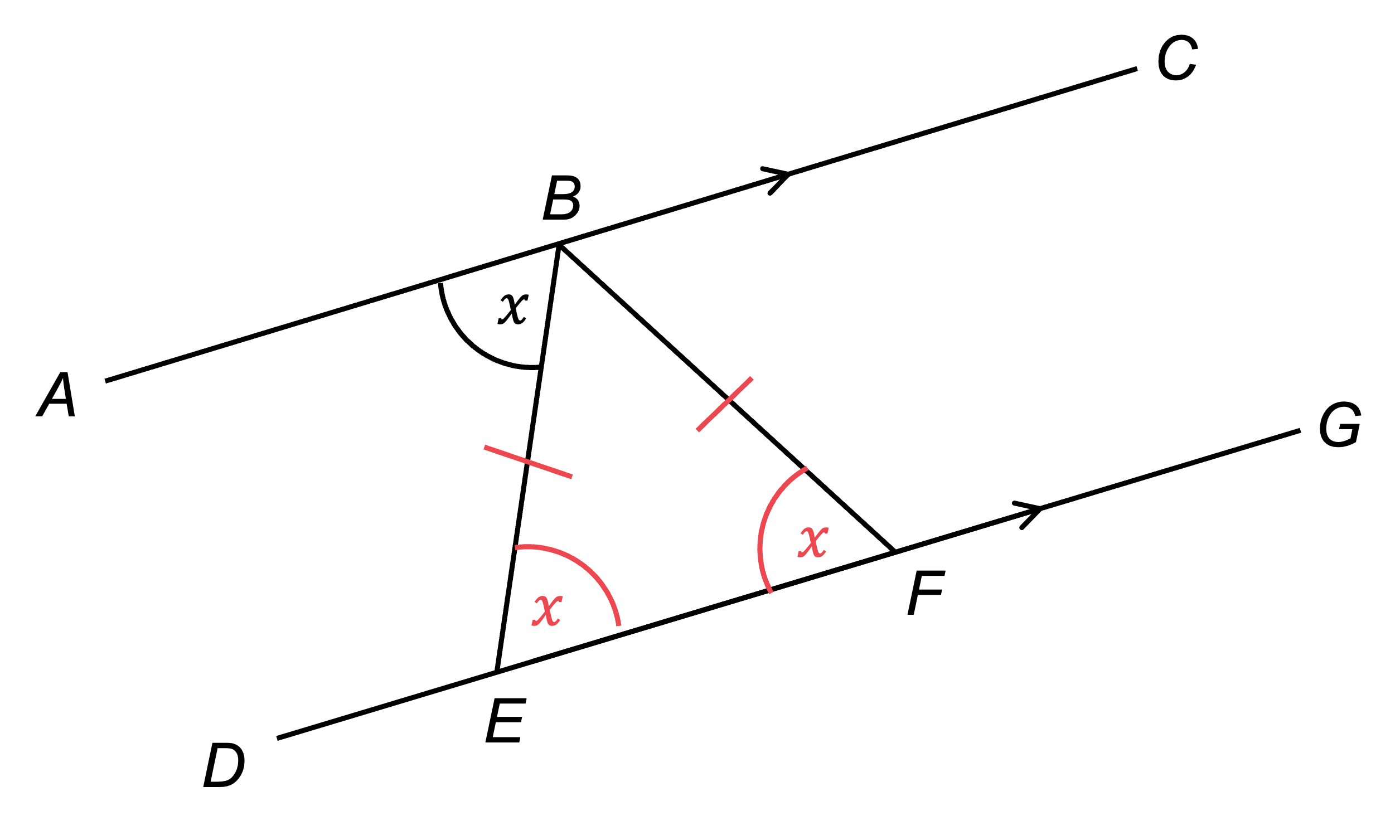
Write the fact, and the reason using the key mathematical vocabulary
angle BFE = , base angles of an isosceles triangle are equal
Now we can see that angle EBF is the last remaining angle in a triangle, and as the angles in a triangle sum to 180, angle EBF =
Write the fact, and the reason using the key mathematical vocabulary
angle EBF = , angles in a triangle sum to 180

Unlock more, it's free!
Did this page help you?