IGCSEMathsEdexcelMaths A (Modular)Higher Unit 2Revision NotesGeometryCircle TheoremsIntersecting Chord Theorem

Intersecting Chord Theorem (Edexcel IGCSE Maths A (Modular))

Revision Note

Flashcards
Amber

Written by: Amber

Reviewed by: Dan Finlay

Did this video help you?

Intersecting Chord Theorem

What is the intersecting chord theorem?

  • For two chords, AB and CD that meet at point P

    • AP : PD ≡ CP : PB

    • Ratio of longer lengths (of chords) ≡ Ratio of shorter lengths (of chords)

    • This can also be written as AP × PB = CP × PD

  • You do not need to know the proof of this theorem

  • This theorem is closely related to similar shapes

Chords AB and CD intersect at point P inside a circle. AP x PB = CP x PD and ab = cd.

How do I use the intersecting chord theorem to solve problems?

  • If two chords intersect, you can find a missing length using the intersecting chord theorem

    • You can usually choose to solve the problem either using multiplication (AP × PB = CP × PD) or using ratio (AP : PD ≡ CP : PB)

  • Carefully keep track of which distance is associated with each part of each chord

Diagram of a circle with intersecting chords AB and CD. Lengths AP = 12, PB = 5, CP = 4, and PD = x. Solution shows x = 15 using ratios and multiplication rules.

What if the lengths are algebraic?

  • If any of the lengths are algebraic expressions, use the fact that AP × PB = CP × PD to form an equation and then solve it

algebraic solution using intersecting chord theorem

Worked Example

The diagram below shows a circle with centre O and two chords, PQ and RS.

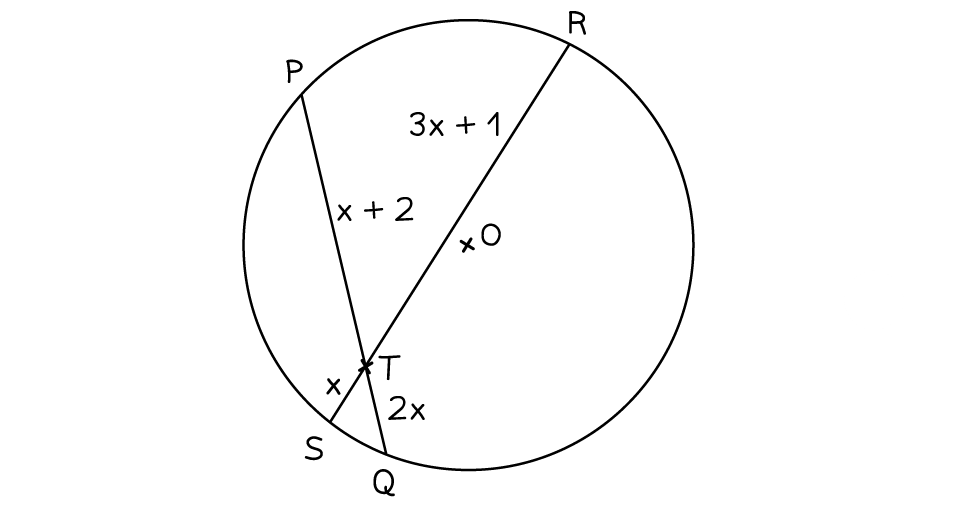
Diagram of intersecting chord theorem for worked example

The chords PQ and RS meet at the point T.

(a) Find the possible value(s) of x.

Using the intersecting chord theorem which states that

P T cross times T Q equals R T cross times T S

Fill in the information from the diagram

open parentheses x plus 2 close parentheses 2 x equals open parentheses 3 x plus 1 close parentheses x

Simplify

table row cell 2 x squared plus 4 x end cell equals cell 3 x squared plus x end cell row 0 equals cell x squared minus 3 x end cell end table

Solve by factorising

0 equals x open parentheses x minus 3 close parentheses x equals 0 space or space x equals 3

Consider if both answers are possible

x refers to a length, so cannot be zero

x equals 3

(b) Hence, or otherwise, write down the simplified ratio of PT:RT.

Method 1

Substitute the found value of x into the expressions on the diagram for PT and RT

P T equals x plus 2 equals 5 R T equals 3 x plus 1 equals 10

Write as a ratio PT:RT

5 colon 10

Simplify

1 colon 2

Method 2

Using the ratio form of the intersecting chord theorem, and the expressions on the diagram

table row cell P T colon R T space end cell equals cell space T S colon T Q end cell row cell open parentheses x plus 2 close parentheses space colon space open parentheses 3 x plus 1 close parentheses space end cell equals cell space open parentheses x close parentheses space colon space open parentheses 2 x close parentheses end cell end table

This shows that the ratio of PT:RT is the same as the ratio of TS:TQ

P T colon R T x space colon space 2 x 1 colon 2

1 colon 2

Intersecting Chord Theorem (External)

What is the external case of the intersecting chord theorem?

  • The intersecting secant theorem is the mathematical name given to the external case of the intersecting chord theorem

    • A secant is a line which extends through a circle cutting the circumference at two points

  • It occurs when two chords intersect outside of the circle

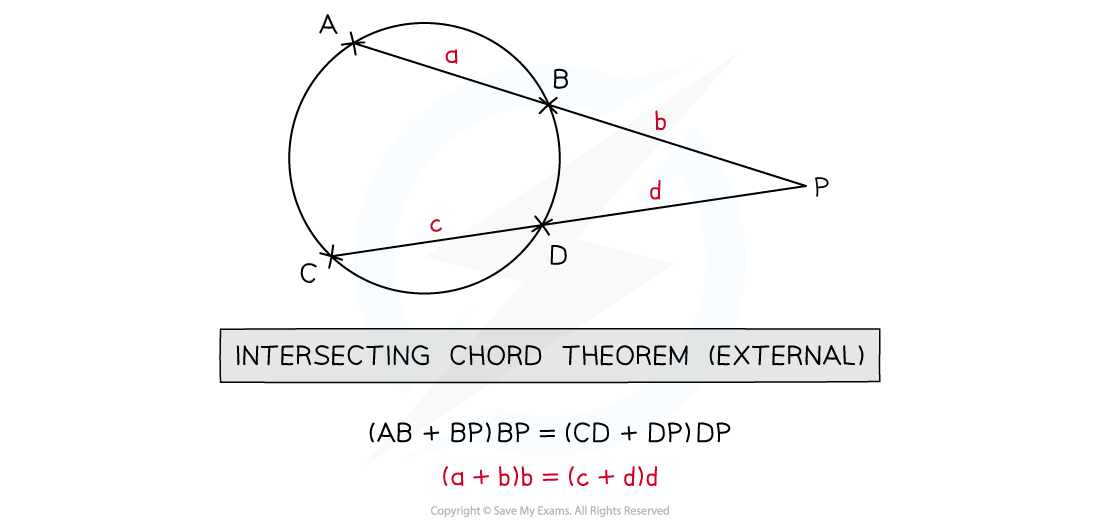
    • For two chords, AB and CD that extend and meet at point P outside of the circle

      • AP : PD ≡ CP : PB where AP = AB + BP and CP = CD + DP

      • Therefore (AB + BP) : PD ≡ (CD + DP) : PB

    • A more practical way to deal with most problems involving the intersecting secant theorem is

      • BP(AB + BP) = DP(CD + DP)

Diagram illustrating the external intersecting chord theorem, showing circle with chords AB, CD intersecting at external point P, and relevant equations.

How do I use the intersecting secant theorem to solve problems?

  • If two chords intersect outside of a circle, you can find a missing length using the intersecting secant theorem

    • Substitute the values into the multiplication formula

    • BP(AB + BP) = DP(CD + DP)

  • If any of the lengths are algebraic expressions, an equation will be formed which can then be solved

Worked Example

In the diagram below, A, B, C and D are points on a circle.

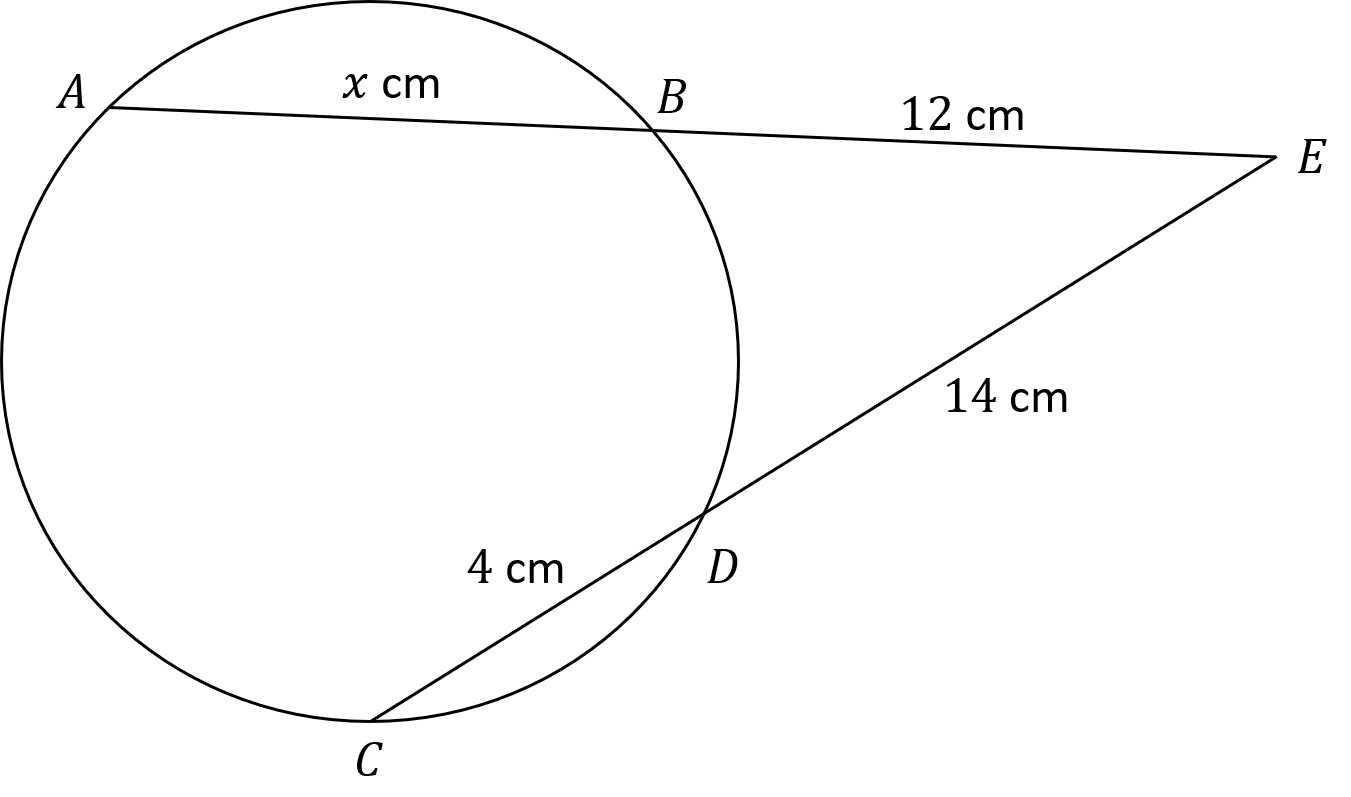
diagram for worked example for intersecting chord theorem

ABE and CDE  are straight lines.
AB = x cm
BE  = 12 cm
CD  = 4 cm
DE  = 14 cm

Work out the value of x.

Using the properties of Intersecting Chords (external intersection)

A B cross times A E equals C D cross times C E space

Or equivalently

B E cross times open parentheses A B plus B E close parentheses equals D E cross times open parentheses C D plus D E close parentheses

Substitute the values from the diagram

12 cross times open parentheses 12 space plus space x close parentheses equals 14 cross times open parentheses space 4 plus space 14 close parentheses

Solve for x

table row cell 12 open parentheses 12 space plus space x close parentheses space end cell equals cell space 252 end cell row cell 12 plus x end cell equals 21 row x equals 9 end table

x equals 9

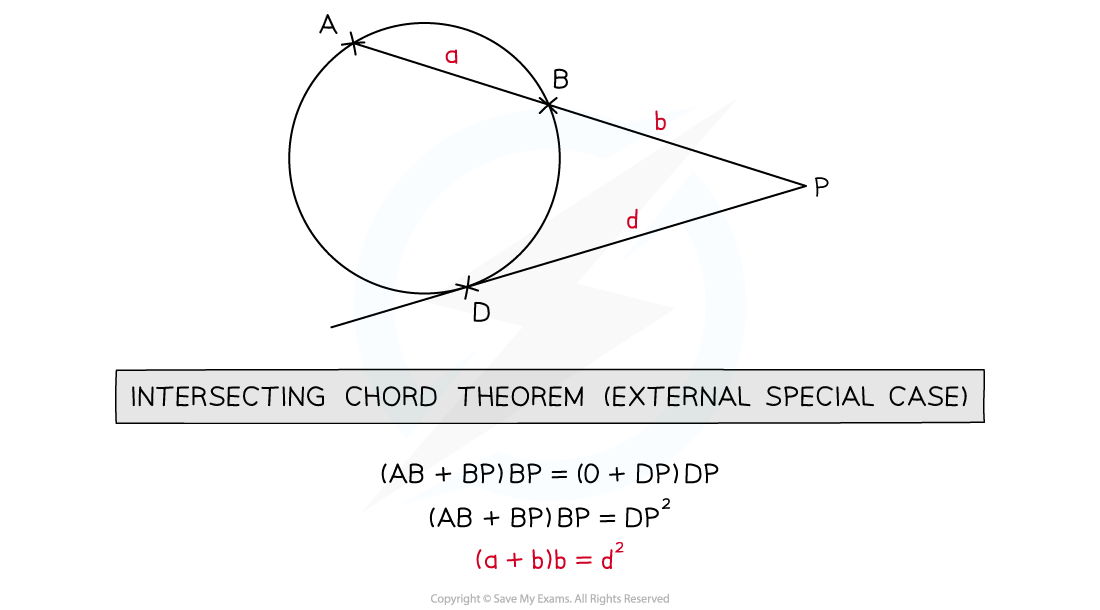
What if one of the lines is a tangent?

  • A special case of the intersecting secant theorem is when one of the lines is a tangent, rather than a secant

    • A tangent touches the circumference of the circle once, rather than intersecting it

    • In this case, one of the lengths becomes zero

      • BP(AB + BP) = DP(0 + DP)

      • BP(AB + BP) = DP2

A diagram illustrating the intersecting chord theorem when one of the chords is a tangent. Equations: (a+b)b = d^2 and (AB+BP)BP = DP^2.

Worked Example

In the diagram below, A, B, and C are points on a circle.

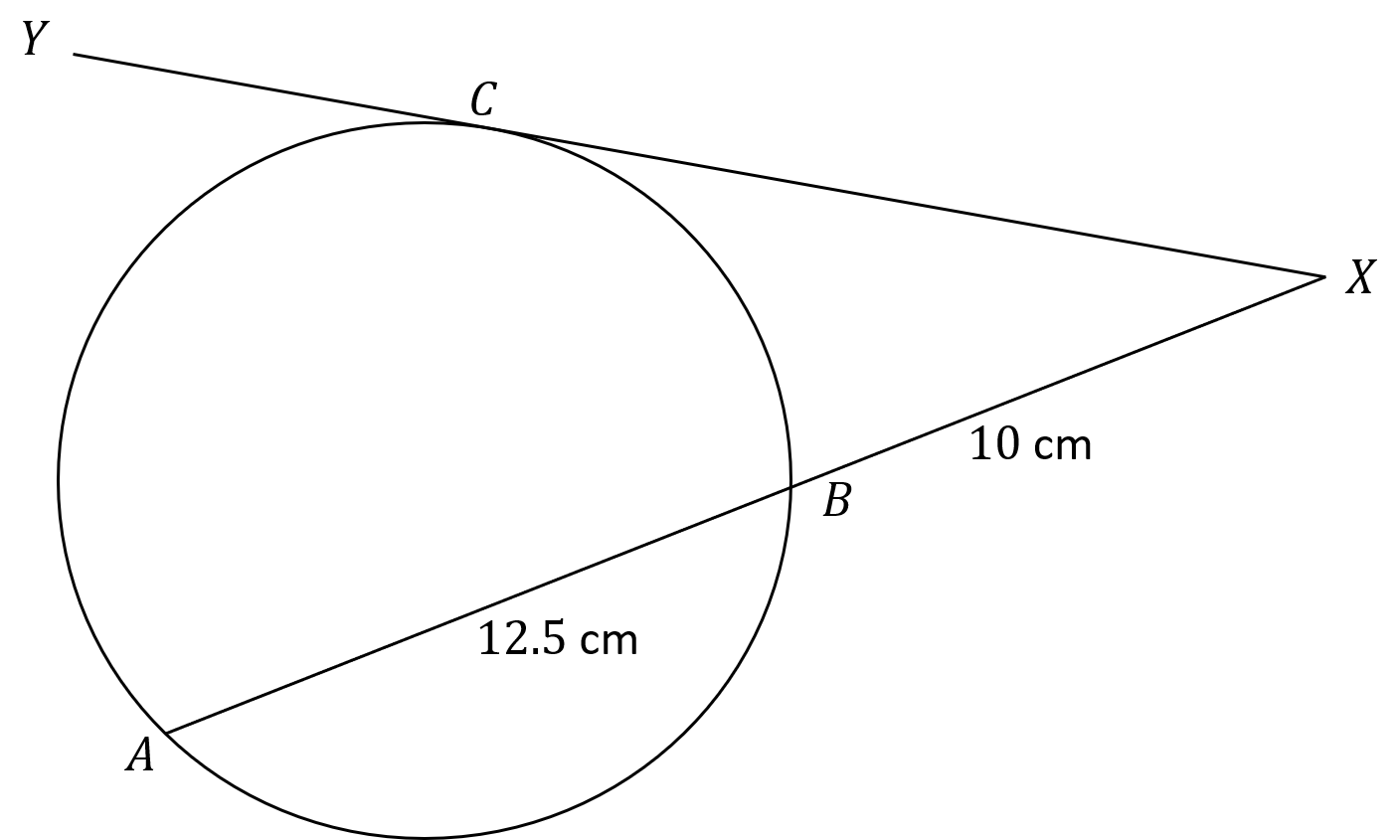
diagram for worked example for special case of intersecting chord theorem where one chord is a tangent

ABX  is a straight line.
YCX  is a tangent to the circle.
AB  = 12.5 cm
BE  = 10 cm

Work out the length of CX.

This is a special case of the properties of Intersecting Chords (external intersection), where one of the lines is a tangent, and therefore one of the line segments has length zero

B X cross times open parentheses A B plus B X close parentheses equals C X cross times open parentheses C X plus 0 close parentheses

Substitute the values from the diagram

10 cross times open parentheses 12.5 plus 10 close parentheses equals C X cross times open parentheses C X plus 0 close parentheses

Simplify and solve for C X

table row cell 10 space open parentheses 22.5 close parentheses space end cell equals cell space open parentheses C X close parentheses squared end cell row cell 225 space end cell equals cell space open parentheses C X close parentheses squared end cell row cell square root of 225 end cell equals cell C X end cell row 15 equals cell C X end cell end table

CX = 15 cm




Last updated:

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Flashcards

    Did this page help you?

    Previous:Theorems with Chords & TangentsNext:Angles in Cyclic Quadrilaterals
    Author
    Reviewer
    Amber

    Author: Amber

    Expertise: Maths

    Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.