Similar Areas & Volumes (Edexcel IGCSE Maths A (Modular))

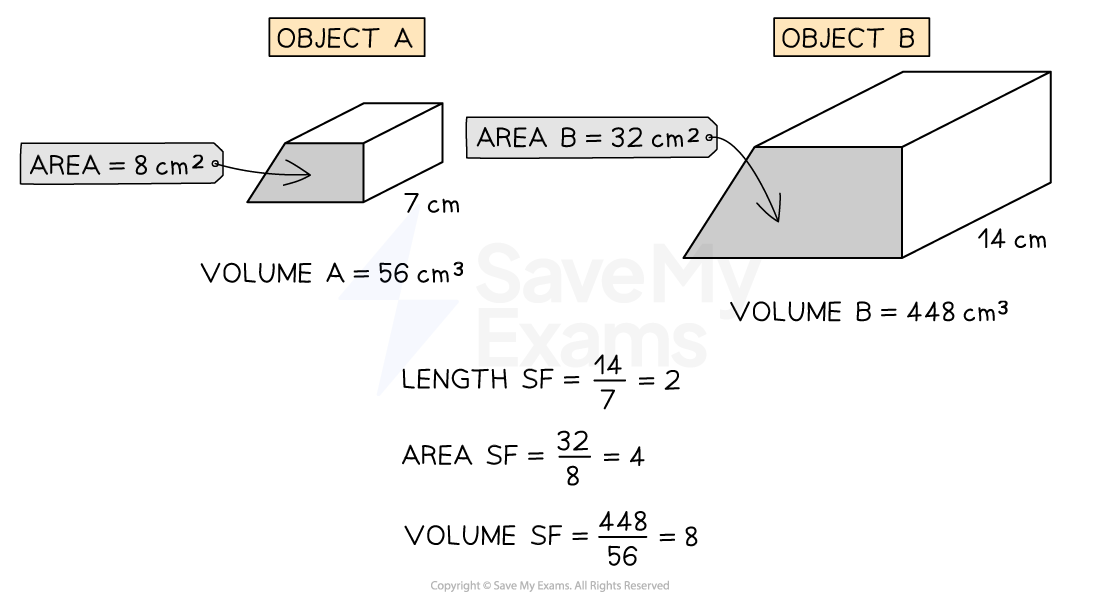
Similar Areas & Volumes

What are similar shapes?

• Two shapes are mathematically similar if one is an enlargement of the other

• If the lengths of two similar shapes are linked by the scale factor, k

  • Equivalent areas are linked by an area factor, k²

  • Equivalent volumes are linked by a volume factor, k³

• The scale factor (SF) for a given quantity (length, area or volume), can be found using the formula:

• An object could be made either bigger or smaller by a scale factor

  • When k > 1, the object is getting bigger

    • This is also true for k² > 1 and k³ > 1

  • When 0 < k < 1, the object is getting smaller

    • This is also true for 0< k² < 1 and 0 < k³ < 1

How do I work with similar shapes involving area or volume?

• STEP 1
  Identify the equivalent known quantities

  • Recognise if the quantities are lengths, areas or volumes

• STEP 2
  Find the scale factor from two known lengths, areas or volumes

  • 

  • For two lengths, k = length SF

  • For two areas, k² = area SF

  • For two volumes, k³ = volume SF

• STEP 3
  Check the scale factor

  • SF > 1 if getting bigger

  • 0 < SF < 1 if getting smaller

• STEP 4
  If necessary, use the scale factor you have found to find other scale factors

  • If you have the length scale factor

    • 

    • 

  • If you have the area scale factor

    • 

    • Find the volume scale factor by finding the length scale factor first

  • If you have the volume scale factor

    • 

    • Find the area scale factor by finding the length scale factor first

• STEP 5
  Multiply or divide by relevant scale factor to find a new quantity