IGCSEMathsEdexcelMaths A (Modular)Higher Unit 2Revision NotesGeometryAngles in Polygons & Parallel LinesBasic Angle Properties

Basic Angle Properties (Edexcel IGCSE Maths A (Modular))

Revision Note

Flashcards
Jamie Wood

Written by: Jamie Wood

Reviewed by: Dan Finlay

Edexcel Maths A (Modular): Higher Unit 2Cambridge (CIE) International Maths: ExtendedCambridge (CIE) International Maths: Core

Basic Angle Properties

What are the basic angle properties?

  • Angles around a point add up to 360°

  • Angles that form a straight line add up to 180°

  • Vertically opposite angles are equal

    • Vertically opposite angles occur when two lines intersect, as in the diagram below

Vertically opposite angles

Worked Example

The diagram below shows three straight lines intersecting at a point.

Basic angle properties worked example question

Find the values of x and y.

Vertically opposite angles between two intersecting lines are equal

x equals 25

Angles that meet on a straight line add up to 180°

table row cell x plus y plus 98 end cell equals cell 180 space end cell row cell 25 plus y plus 98 end cell equals 180 row cell 123 plus y end cell equals 180 end table

Solve to find y

y equals 180 minus 123 y equals 57

bold italic x bold equals bold 25 bold comma bold space bold italic y bold equals bold 57

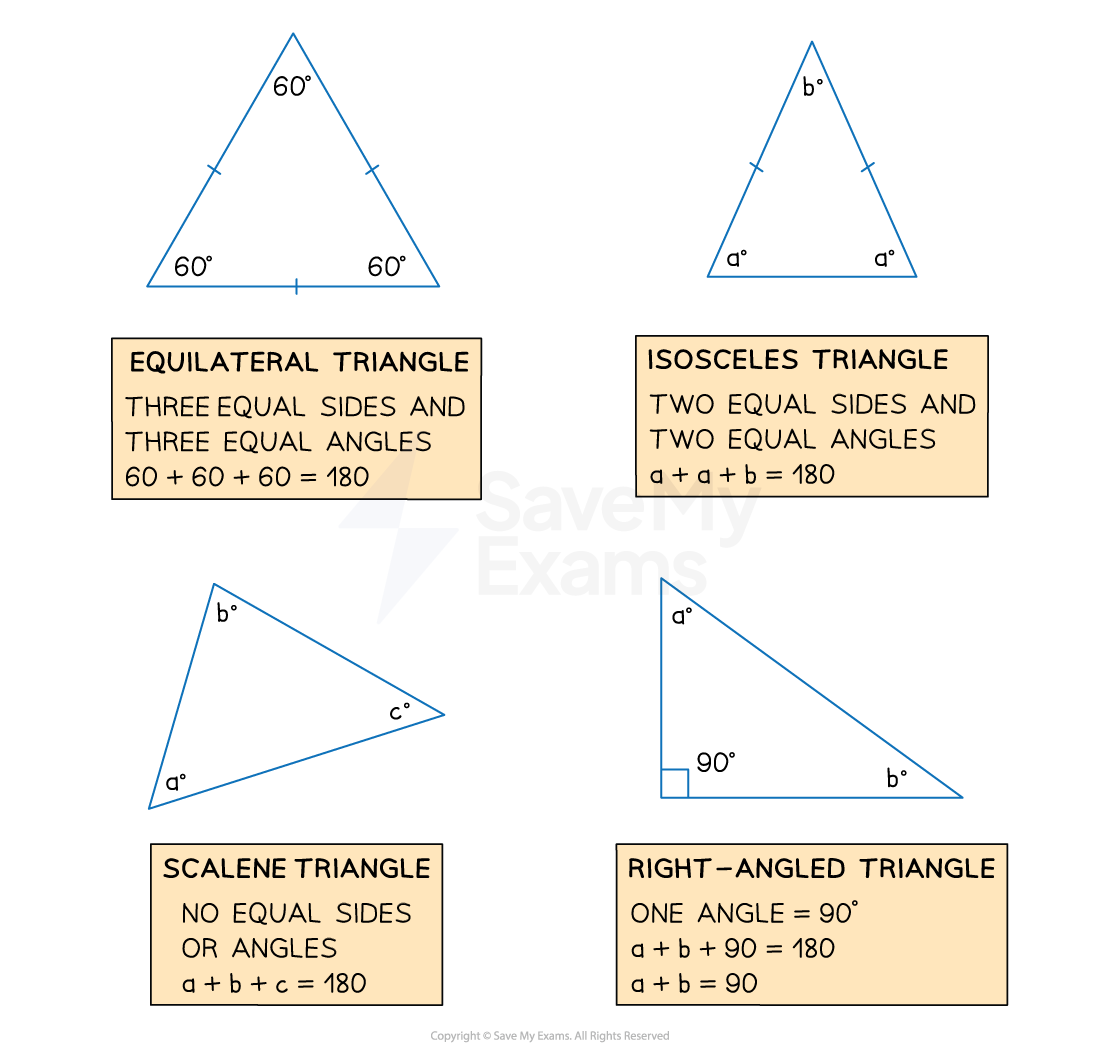
What are the angle properties of triangles?

  • The three interior angles inside any triangle add up to 180°

  • If the triangle is isosceles then two angles will be equal

    • These will be the two angles opposite the two sides of equal length

  • If the triangle is equilateral then all three angles will be equal

    • Each angle will equal 60°

  • A right-angled triangle has one 90° angle

angle properties of triangles

Examiner Tips and Tricks

  • Find all the missing angles that you can using the angles that are given to you in a question

    • They might not seem to help you straight away but having more angles will lead you to find the angle you need

Worked Example

The diagram below is formed using three straight lines.

Find the value of x.

Triangle angle properties worked example question

Label the other missing angles inside the triangle
 

Triangle angle properties worked example working

Vertically opposite angles between two intersecting lines are equal

y equals 60

Angles that meet on a straight line add up to 180°

table row cell z plus 130 end cell equals cell 180 space end cell row z equals 50 end table

Interior angles in a triangle add up to 180°

table row cell x plus 60 plus 50 end cell equals 180 row cell x plus 110 end cell equals 180 end table

bold italic x bold equals bold 70

What are the angle properties of quadrilaterals?

  • The four interior angles inside any quadrilateral add up to 360°

  • If the quadrilateral is a square or a rectangle then all the angles are equal to 90°

  • You can use any symmetries of the quadrilateral to identify other equal angles

    • For a parallelogram or rhombus, opposite angles are equal

    • For a kite, one pair of opposite angles are equal

Quadrilateral angle properties worked example question

Worked Example

The diagram below shows an irregular quadrilateral.

Find the value of y.

Quadrilateral angle properties worked example question

Find the missing angle inside the quadrilateral using the rule 'angles in a quadrilateral add up to 360°'

First, add together the three given angles

97 plus 115 plus 85 equals 297

Subtract the answer from 360°

table row cell 360 minus 297 end cell equals 63 end table

Add this to the diagram

Quadrilateral angle properties worked example working

Angles on a straight line add up to 180°, so subtract the answer from 180°

table row cell y plus 63 end cell equals 180 row y equals cell 180 minus 63 end cell row y equals 117 end table

bold italic y bold equals bold 117

Last updated:

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Flashcards

    Did this page help you?

    Previous:Using Differentiation for KinematicsNext:Angles in Polygons
    Author
    Reviewer
    Jamie Wood

    Author: Jamie Wood

    Expertise: Maths

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.