Revision NotesFlashcardsPast Papers
IGCSEMathsEdexcelMaths A (Modular)Higher Unit 2Revision NotesGeometryAngles in Polygons & Parallel LinesAngles in Polygons

Angles in Polygons (Edexcel IGCSE Maths A (Modular))

Revision Note

Jamie Wood

Written by: Jamie Wood

Reviewed by: Dan Finlay

Edexcel Maths A (Modular): Higher Unit 2Cambridge (CIE) International Maths: ExtendedCambridge (CIE) International Maths: CoreCambridge (CIE) Maths: CoreCambridge (CIE) Maths: ExtendedEdexcel Maths A: Higher

Did this video help you?

Angles in Polygons

What is a polygon?

  • A polygon is a 2D shape with n straight sides

    • A triangle is a polygon with 3 sides

    • A quadrilateral polygon with 4 sides

    • A pentagon is a polygon with 5 sides

  • In a regular polygon all the sides are the same length and all the angles are the same size

    • A regular polygon with 3 sides is an equilateral triangle

    • A regular polygon with 4 sides is a square

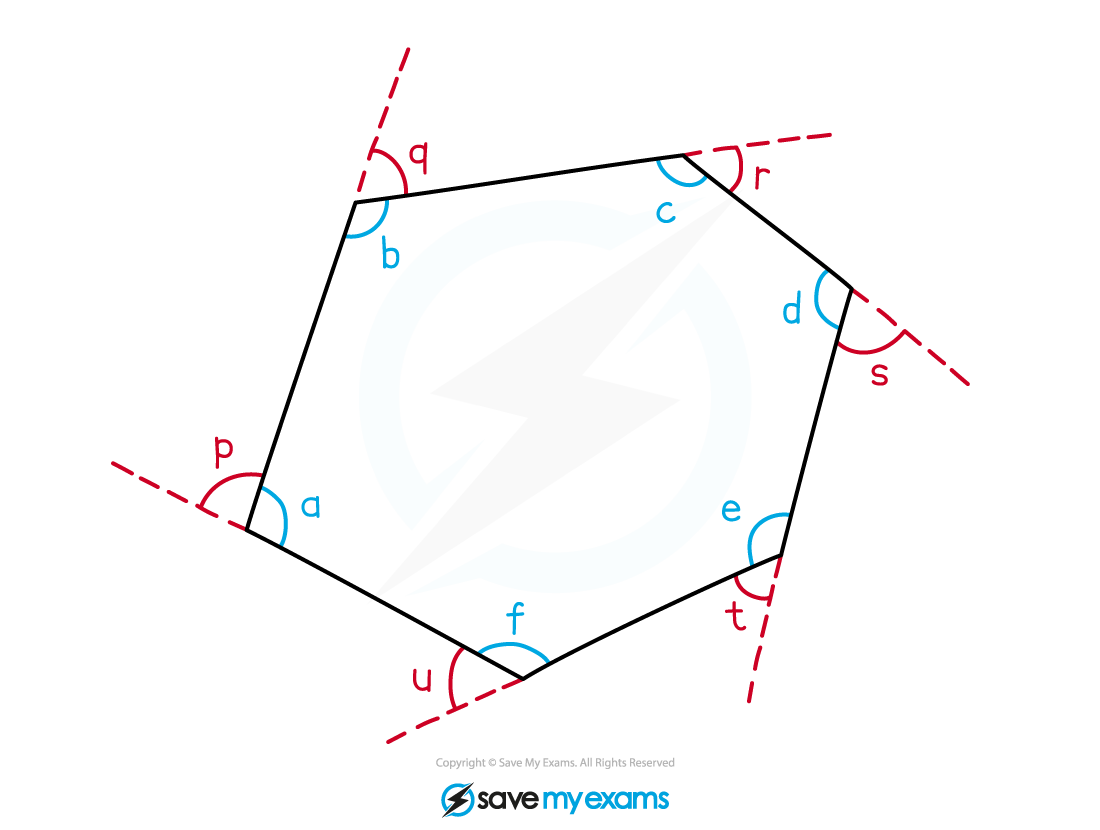
What are the interior angles and the exterior angles of a polygon?

  • Interior angles are the angles inside a polygon at the corners

  • The exterior angle at a corner is the angle needed to make a straight line with the interior angles

    • It is not the angle that forms a full turn at the corner

  • The interior angle and exterior angle add up to 180° at each corner

interior and exterior angles summing to 180 degrees
Interior and exterior angles in a hexagon

What is the sum of the interior angles in a polygon?

  • To find the sum of the interior angles in a polygon of n sides, use the rule

    • Sum of interior angles = 180 degree space cross times space left parenthesis n space – space 2 right parenthesis

      • This formula comes from the fact that n-sided polygons can be split into n minus 2 triangles

  • Remember the sums for these polygons

    • The interior angles of a triangle add up to 180°

    • The interior angles of a quadrilateral add up to 360°

    • The interior angles of a pentagon add up to 540°

What is the sum of the exterior angles in a polygon?

  • The exterior angles in any polygon always sum to 360°

How do I find the size of an interior or exterior angle in a regular polygon?

  • To find the size of an interior angle in a regular polygon:

    • Find the sum of the interior angles

      • For a pentagon: 180 degree cross times open parentheses 5 minus 2 close parentheses space equals space 540 degree

    • Divide by the number of sides (n)

      • For a pentagon: 540 degree divided by 5 equals 108 degree

  • To find the size of an exterior angle in a regular polygon:

    • Divide 360° by the number of sides (n)

      • For a pentagon: 360 degree divided by 5 equals 72 degree

  • The interior angle and exterior angle add to 180°

    • Subtract the exterior angle from 180° to find the interior angle

    • Subtract the interior angle from 180° to find the exterior angle

Regular Polygon

Number of Sides

Sum of Interior Angles

Size of Interior Angle

Size of Exterior Angle

Equilateral Triangle

3

180°

60°

120°

Square

4

360°

90°

90°

Regular Pentagon

5

540°

108°

72°

Regular Hexagon

6

720°

120°

60°

Regular Octagon

8

1080°

135°

45°

Regular Decagon

10

1440°

144°

36°

How do I find a missing angle in a polygon?

  • STEP 1
    Calculate the sum of the interior angles for the polygon

    • Use the formula 180 degree cross times open parentheses n minus 2 close parentheses

  • STEP 2
    Subtract the other interior angles in the polygon

Examiner Tips and Tricks

  • Make sure you identify whether you are dealing with a regular or irregular polygon before you start a question

  • Finding the sum of the interior angles using 180 cross times open parentheses n minus 2 close parentheses can often be a good starting point for finding missing angles

Worked Example

The exterior angle of a regular polygon is 45°.

Write down the name of the polygon.

The formula for the exterior angle of a regular polygon is Exterior space Angle equals fraction numerator 360 degree over denominator n end fraction 

Substitute the 45 for the exterior angle

45 degree equals fraction numerator 360 degree over denominator n end fraction

Solve by rearranging

table row n equals cell 360 over 45 end cell row n equals 8 end table

Write down the name of a shape with 8 sides

Regular Octagon

Last updated:

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Flashcards

    Did this page help you?

    Previous:Basic Angle PropertiesNext:Angles in Parallel Lines
    Author
    Reviewer
    Jamie Wood

    Author: Jamie Wood

    Expertise: Maths

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.