Translations of Graphs (Edexcel IGCSE Maths A (Modular)): Revision Note

Written by: Naomi C

Reviewed by: Dan Finlay

Updated on 18 October 2024

Did this video help you?

Translations of Graphs

What are translations of graphs?

The equation of a graph can be changed in certain ways
- This has an effect on the graph
  - How a graph changes is called a graph transformation
A translation is a type of graph transformation that shifts (moves) a graph (up or down, left or right) in the xy plane
- The shape, size, and orientation of the graph remain unchanged

A particular translation is specified by a translation vector

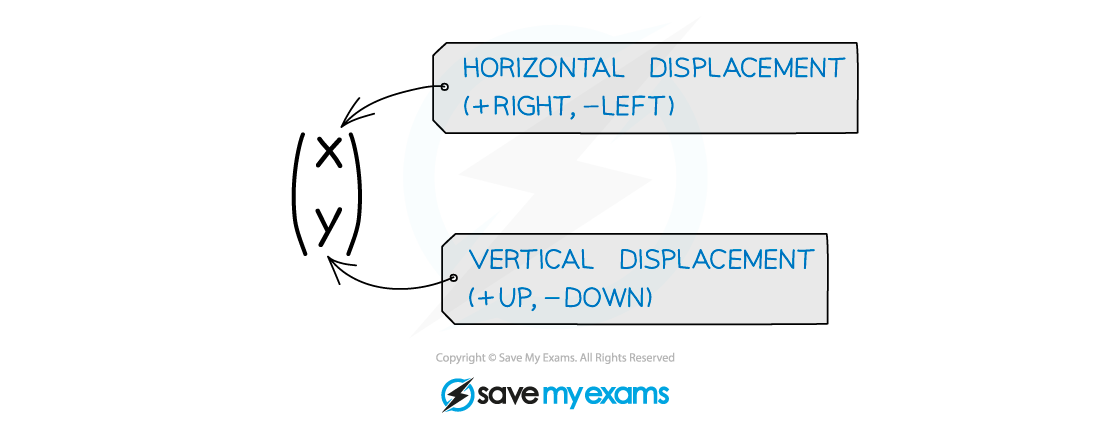
How do I translate graphs?

Let $y = f (x)$ be the equation of the original graph

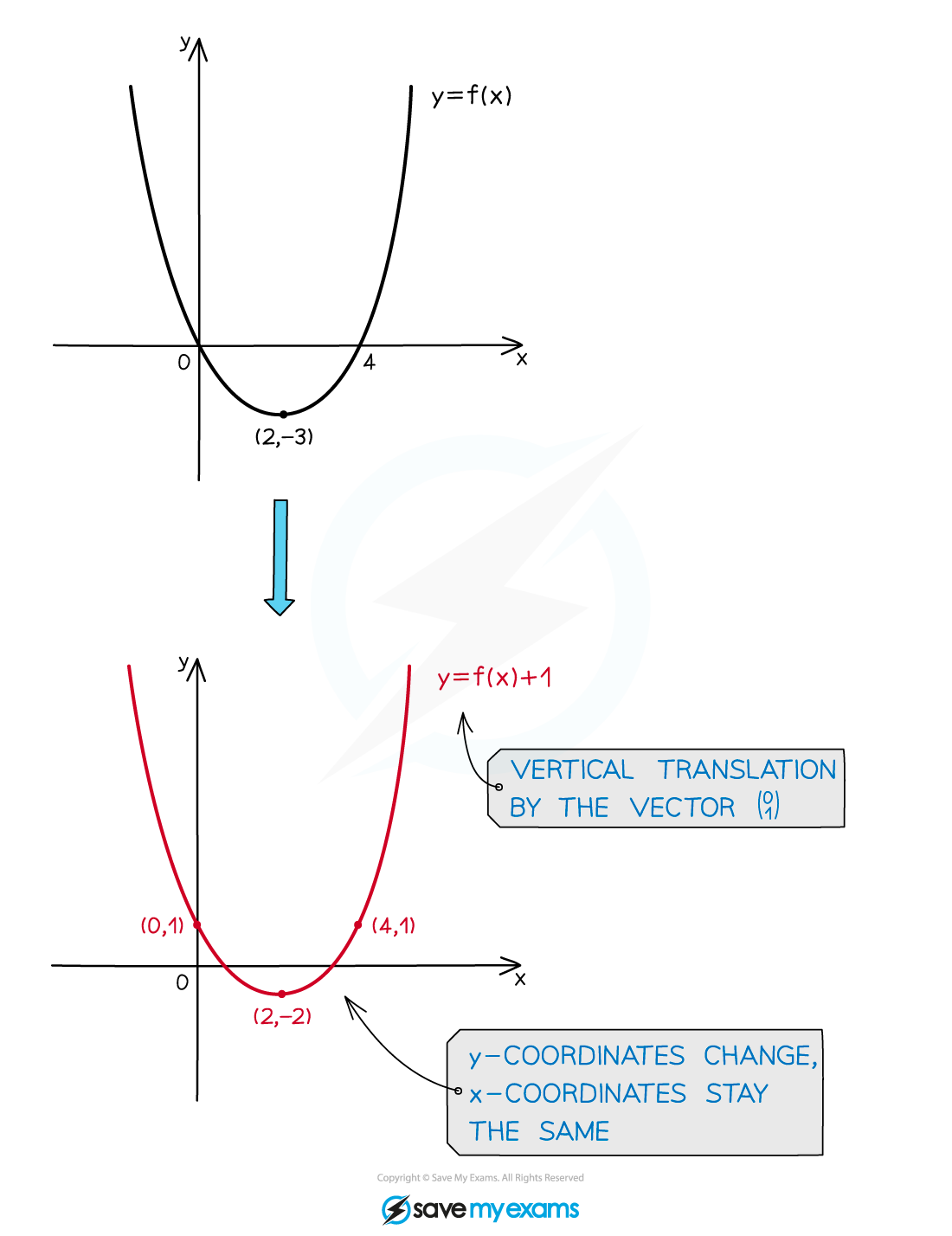
Vertical translations: y=f(x) + a

$y = f (x) + a$ is a vertical translation by the vector $(\begin{matrix} 0 \\ a \end{matrix})$
- The graph moves up for positive values of $a$
- The graph moves down for negative values of $a$
- The x-coordinates stay the same

Vertical translation of a graph by the vector (0, 1)

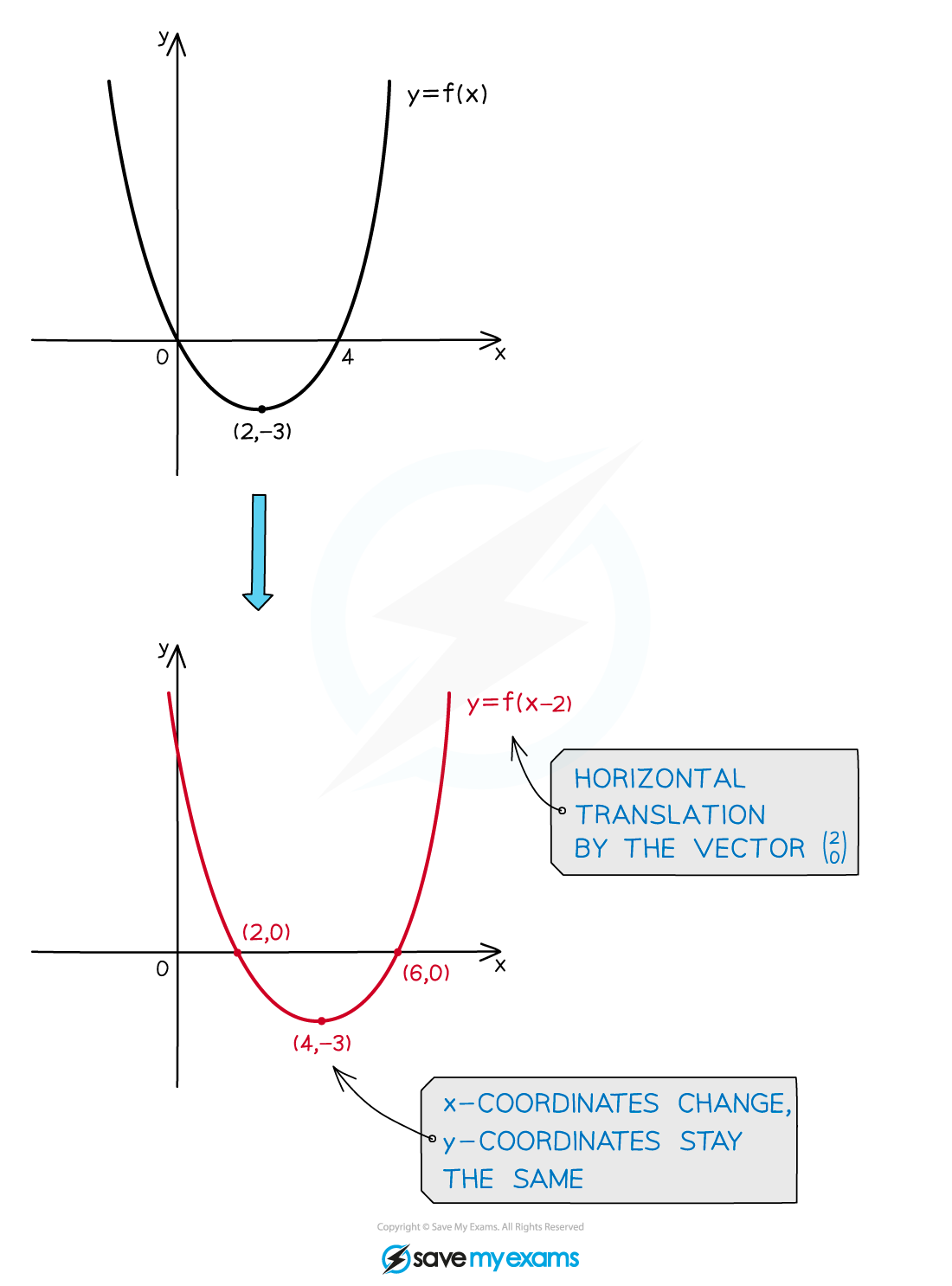
Horizontal translations: y=f(x + a)

$y = f (x + a)$ is a horizontal translation by the vector $(\begin{matrix} - a \\ 0 \end{matrix})$
- The graph moves left for positive values of $a$
  - This is often the opposite direction to which people expect
- The graph moves right for negative values of $a$
- The y-coordinates stay the same

Horizontal translation of a graph by the vector (2, 0)

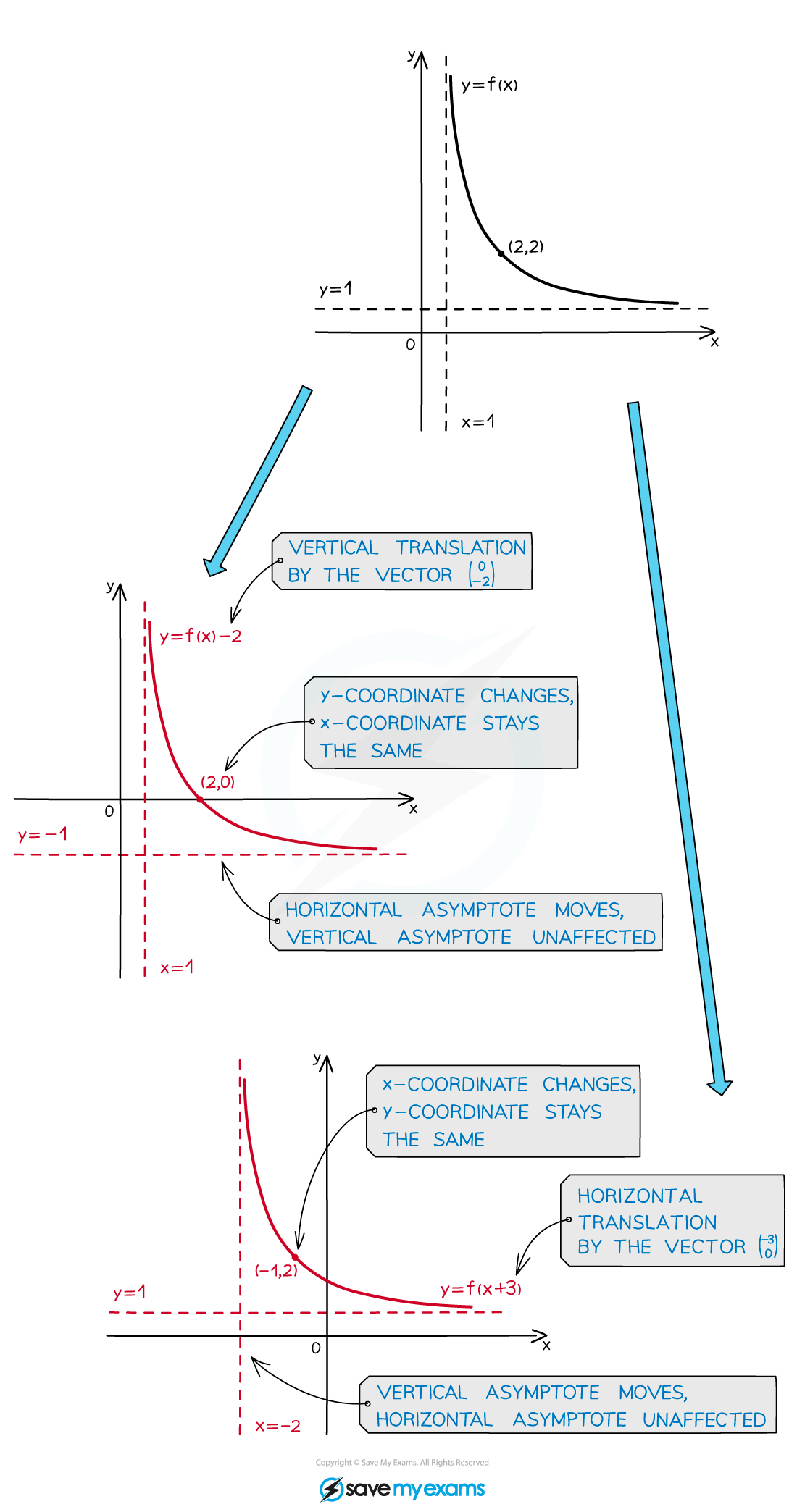
What happens to asymptotes when a graph is translated?

Any asymptotes of f(x) are also translated
- An asymptote parallel to the direction of translation will not be affected

How does a translation affect the equation of the graph?

For a horizontal translation $y = f (x - a)$ of the graph $y = f (x)$
- $a$ is subtracted from $x$ throughout the equation
- Every instance of $x$ in the equation is replaced with $(x - a)$
E.g. the graph $y = x^{2} - 3 x + 7$ undergoes a translation of 6 units to the right
- $y = f (x)$ becomes $y = f (x - 6)$
- $x$ is replaced throughout the equation by $(x - 6)$
  - $y = {(x - 6)}^{2} - 3 (x - 6) + 7$ is the new equation
- The equation can be left in this form or expanded and simplified
  - $y = x^{2} - 12 x + 36 - 3 x + 18 + 7$
  - $y = x^{2} - 15 x + 61$
For a vertical translation $y = f (x) + a$ of the graph $y = f (x)$
- $a$ is added to the equation as a whole
E.g. the graph $y = 4 x^{2} + 2 x + 1$ undergoes a translation of 5 units down
- $y = f (x)$ becomes $y = f (x) - 5$
- 5 is subtracted from the equation as a whole
  - $y = 4 x^{2} + 2 x + 1 - 5$
- The equation can be left in this form or simplified
  - $y = 4 x^{2} + 2 x - 4$

How do I apply a combined translation?

For a horizontal translation of $p$ units and vertical translation of $q$ units combined
- $y = f (x)$ becomes $y = f (x - p) + q$
E.g. the graph $y = 3 x^{2}$ undergoes a translation of 2 units up and 1 unit to the left
- $y = f (x)$ will become $y = f (x + 1) + 2$
- $x$ is replaced throughout the equation by $(x + 1)$
- 2 is added to the equation as a whole
  - $y = 3 {(x + 1)}^{2} + 2$

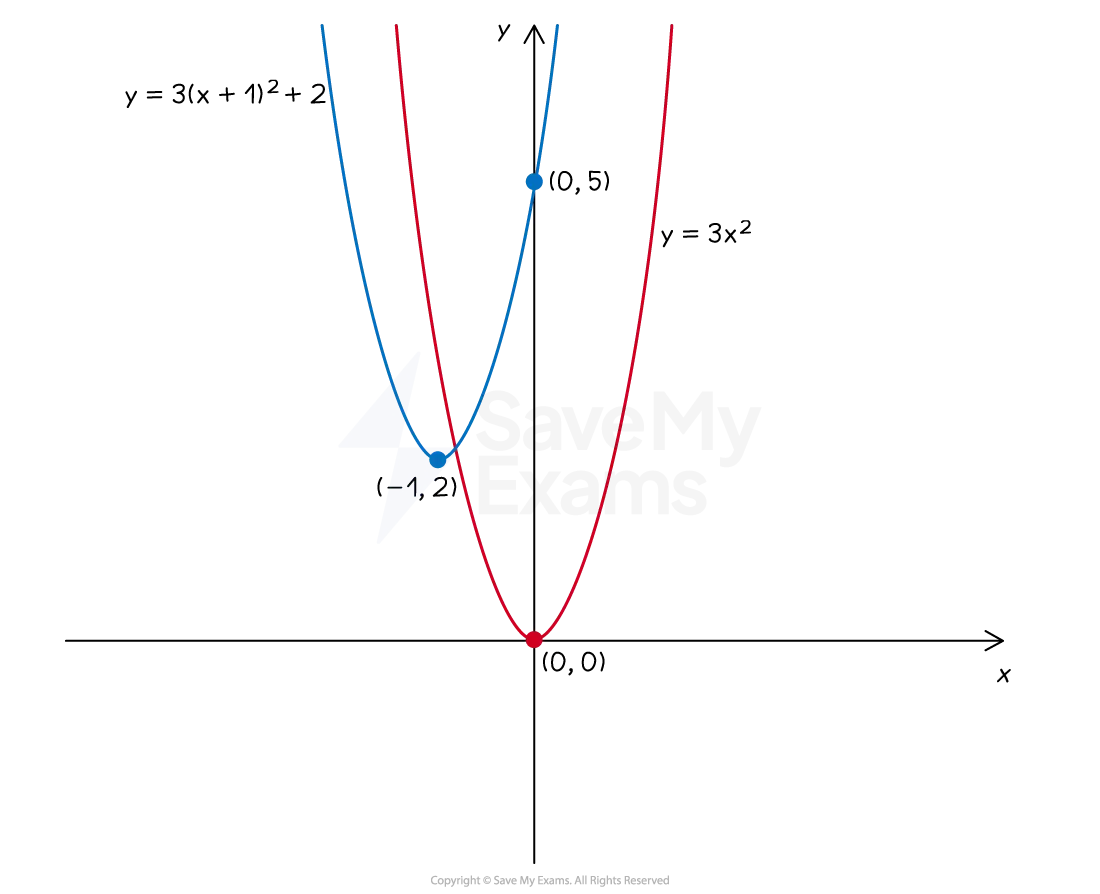
Transformation of the graph y=3x^2 by a horizontal translation of -1 and vertical translation of +2.

Note that when the equation is in the form $y = a {(x - p)}^{2} + q$
- the vertex is $(p, q)$
- the value of $a$ does not affect the vertex coordinates

Worked Example

The diagram below shows the graph of $y = f (x)$ .

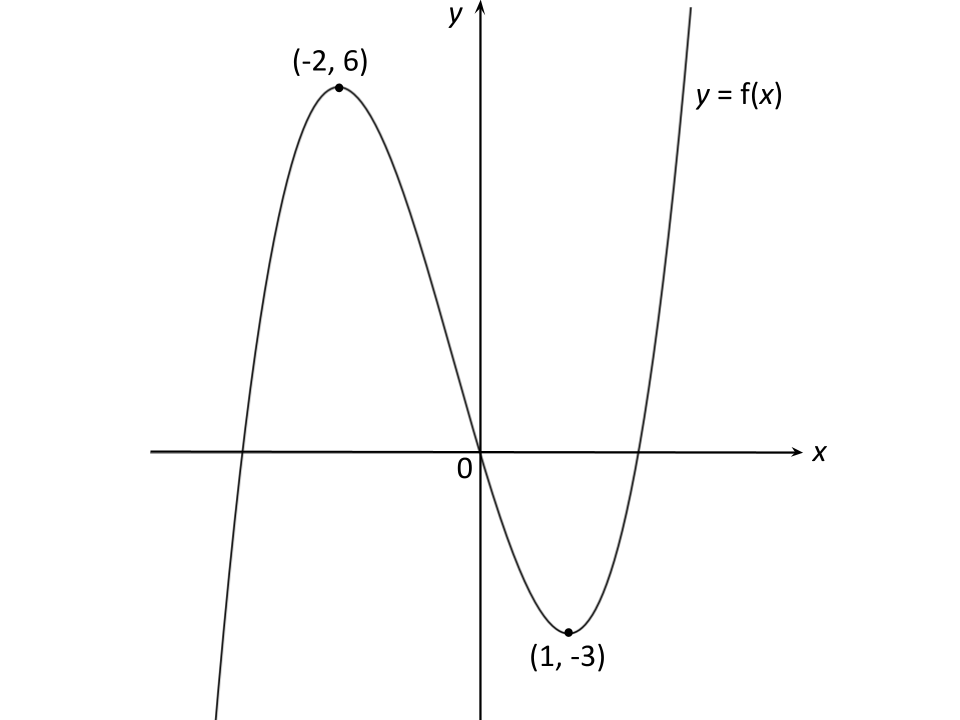
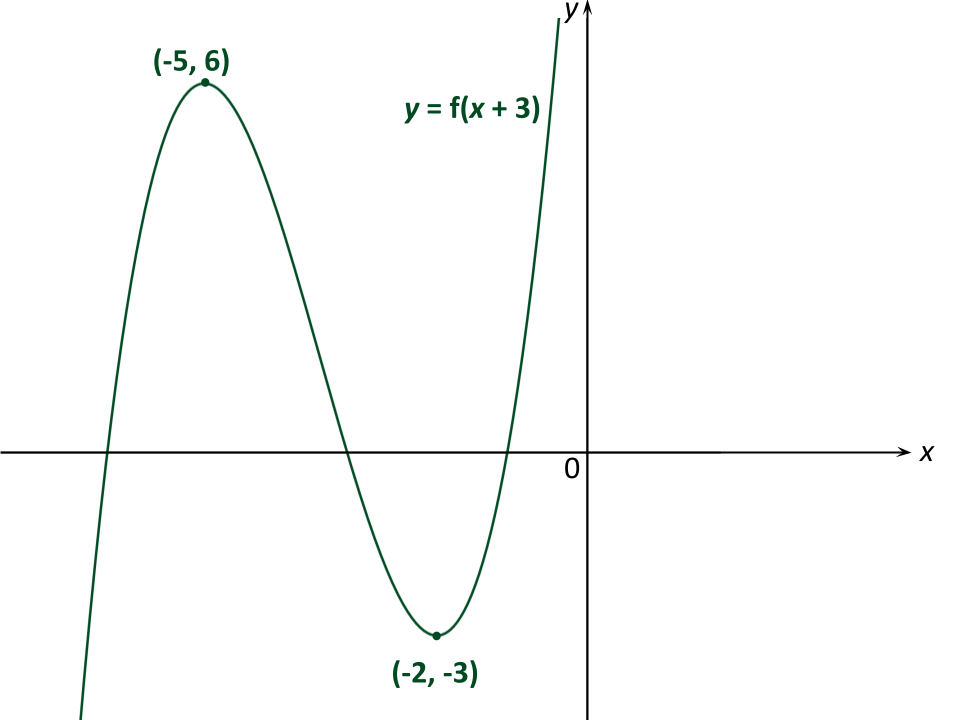
Sketch the graph of $y = f (x + 3)$ .

The transformation of the graph is a horizontal translation with vector $(\begin{matrix} - 3 \\ 0 \end{matrix})$ (3 units to the left)

The x-coordinates of the points change (subtract 3 from each)
The y-coordinates of the points stay the same

You've read 1 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.
Beth
IGCSE Student
This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!
Fathima
A Level Student
Incredible! SO worth my money, the revision notes have everything I need to know and are so easy to understand. I actually enjoy revising! It makes me feel a lot more confident for my GCSEs in a few months.
Kate
GCSE Student
Absolutely brilliant, both my girls used it for A levels and GCSE. It's saves on paper copies, also beneficial exam questions ranked from easy to hard. It's removed a lot of stress from the exams.
Sameera
Parent
Just to say that your resources are the best I have seen and I have been teaching chemistry at different levels for about 40 years
Mark
Chemistry Teacher
Excellent
Read more reviews

Flashcards

Did this page help you?

Previous:Finding Inequalities from RegionsNext:Reflections of Graphs

Number

Prime Factors, HCF & LCM

Prime Factor Decomposition

Uses of Prime Factor Decomposition

HCF & LCM

Standard Form

Converting To & From Standard Form

Operations with Standard Form

Using Percentages

Percentage Increases & Decreases

Reverse Percentages

Compound Interest & Depreciation

Compound Interest

Depreciation

Ratio Toolkit

Introduction to Ratios

Sharing in a Ratio

Working with Proportion

Ratio Problem Solving

Ratios & FDP

Multiple Ratios

Direct & Inverse Proportion

Direct Proportion

Inverse Proportion

Algebra & Sequences

Rearranging Formulas

Formulas where Subject Appears Once

Formulas where Subject Appears Twice

Algebraic Proof

Algebraic Proof

Solving Inequalities

Solving Linear Inequalities

Solving Quadratic Inequalities

Simultaneous Equations

Linear Simultaneous Equations

Quadratic Simultaneous Equations

Forming & Solving Equations

Forming Equations from Shapes

Problem Solving with Equations

Sequences

Introduction to Sequences

Arithmetic Sequences

Sum of an Arithmetic Series

Functions, Graphs & Differentiation

Functions

Introduction to Functions

Domain & Range

Composite Functions

Inverse Functions

Graphing Inequalities

Representing Inequalities as Regions

Finding Inequalities from Regions

Transformations of Graphs

Translations of Graphs

Reflections of Graphs

Stretches of Graphs

Differentiation & Gradients

Finding Gradients of Tangents

Differentiation

Finding Stationary Points & Turning Points

Classifying Stationary Points

Problem Solving with Differentiation

Using Differentiation for Kinematics

Geometry

Angles in Polygons & Parallel Lines

Basic Angle Properties

Angles in Polygons

Angles in Parallel Lines

2D Shapes

Bearings, Scale Drawing & Constructions

Bearings

Scale

Constructing Triangles

Constructions

Circle Theorems

Angles at Centre & Circumference

Angle in a Semicircle

Theorems with Chords & Tangents

Intersecting Chord Theorem

Angles in Cyclic Quadrilaterals