Revision NotesFlashcardsPast Papers
IGCSEMathsEdexcelMaths A (Modular)Higher Unit 2Revision NotesFunctions, Graphs & DifferentiationDifferentiation & GradientsUsing Differentiation for Kinematics

Using Differentiation for Kinematics (Edexcel IGCSE Maths A (Modular))

Revision Note

Mark Curtis

Written by: Mark Curtis

Reviewed by: Dan Finlay

Edexcel Maths A (Modular): Higher Unit 2Edexcel Maths A: Higher

Did this video help you?

Kinematics

What does kinematics mean?

  • Kinematics is the study of the motion of an object

    • It is a branch of Physics

  • Objects are called particles

    • They are modelled as single moving points

  • Over time, the particles move and

    • can be at different distances from a fixed origin (displacement)

    • can move with different speeds in different directions (velocity)

    • can speed up or slow down (acceleration)

What is displacement?

  • The displacement of an object is how far away it is from a fixed origin

    • It can be positive (in front of the origin)

    • or negative (behind the origin)

  • Do not confuse displacement with distance

    • Distance is always positive!

    • Displacement can have a plus-or-minus sign

  • Displacement is given the letter s in kinematics

    • Do not confuse this letter for speed!

    • Displacement is measured in metres

Diagrams showing displacement examples: one particle 4 metres right of point 0, another 5 metres left of point 0. Text explains displacement in each case.

What is a displacement function?

  • The displacement of an object, s metres, can be written as a function of time, t seconds

    • s equals straight f open parentheses t close parentheses

  • Substitute a value of time in to find its displacement at that time

    • For example, s equals 2 t minus t squared plus 1

      • Initially, t equals 0 gives s equals 2 cross times 0 minus 0 squared plus 1 equals 1 (1 metre in front of the origin)

      • After 3 seconds, t equals 3 gives s equals 2 cross times 3 minus 3 squared plus 1 equals negative 2 (2 metres behind the origin)

What is the velocity and how do I find it?

  • Velocity is the speed and direction of an object

    • It is positive if moving forwards

    • It is negative if moving backwards

    • Do not confuse velocity and speed

      • Speed is always positive!

  • To find the velocity of an object, v metres per second, differentiate its displacement function

    • v equals fraction numerator straight d s over denominator straight d t end fraction

  • For example, if s equals t cubed minus 4 t squared plus 2 t then v equals 3 t squared minus 8 t plus 2 (by differentiation)

    • The initial velocity (t equals 0) is v equals 3 cross times 0 squared minus 8 cross times 0 plus 2 equals 2 ms-1

    • The velocity after 1 second (t equals 1) is v equals 3 cross times 1 squared minus 8 cross times 1 plus 2 equals negative 3 ms-1

      • Its speed is 3 ms-1

  • If a velocity is zero at any point in time, it is said to be at instantaneous rest

    • It is stationary (not moving) at that instant in time

      • but not stationary all the time

    • To find the times at which the particle is at rest, set v equals 0 and solve to find t

What is the acceleration and how do I find it?

  • Acceleration is rate at which the velocity changes

    • It is positive if speeding up (when moving forwards)

    • It is negative if slowing down (when moving forwards)

      • A negative acceleration is also called a deceleration

      • The magnitude of acceleration is always positive

  • To find the acceleration of an object, a metres per second per second, differentiate its velocity function

    • a equals fraction numerator straight d v over denominator straight d t end fraction

  • For example, if v equals 3 t squared minus 8 t plus 2 then a equals 6 t minus 8

    • You can substitute times in to find accelerations

  • It the acceleration is always zero then the particle moves at a constant speed

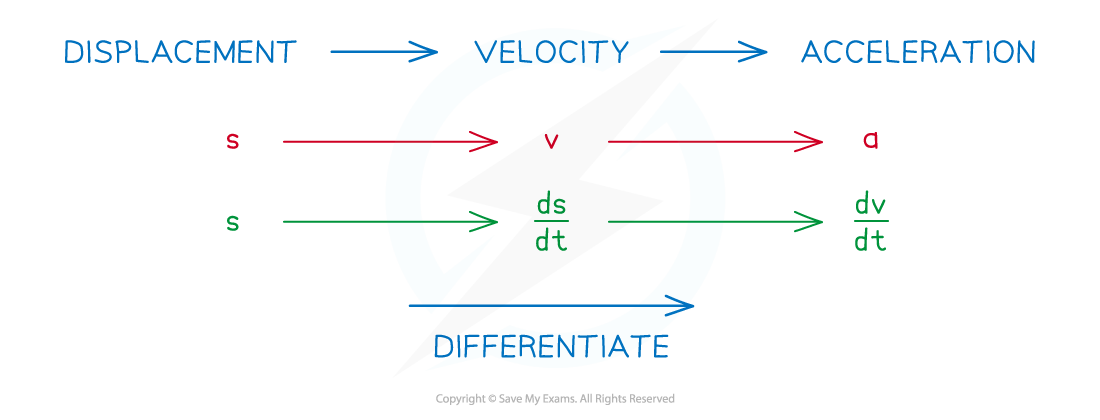
How do I find the acceleration from the displacement?

  • You differentiate displacement to get velocity, then differentiate velocity to get acceleration

    • So you differentiate displacement twice to get acceleration

Diagram showing the relationship between displacement (s), velocity (v), and acceleration (a), with differentiation denoted as ds/dt for velocity and dv/dt for acceleration.

Examiner Tips and Tricks

  • Harder exam questions may jump back and forth between displacement, velocity and acceleration

    • so make sure you use the labels s equals..., v equals... and a equals... to make your working clear

Worked Example

A particle moves along a straight line.

The displacement of the particle from a fixed point, O, on the line at time t seconds is s metres, where

s equals t cubed minus 6 t squared minus 3

(a) Find the initial distance of the particle from O.

Initial means t equals 0
Substitute t equals 0 into s to find the initial displacement

table row s equals cell 0 cubed minus 6 cross times 0 squared minus 3 end cell row blank equals cell negative 3 end cell end table

Distance is always positive, so convert -3 into 3

The particle is initially at a distance of 3 metres from O

(b) Find an expression for the velocity, v ms-1, at time t seconds.

To find the velocity, differentiate the displacement

v equals fraction numerator straight d s over denominator straight d t end fraction equals 3 t squared minus 12 t

This is an expression for the velocity in terms of time, t

v equals 3 t squared minus 12 t ms-1

(c) Find how long, after t equals 0, it takes for the particle to come to rest.

The particle is at rest when v equals 0
Set v equals 0 and solve to find t

0 equals 3 t squared minus 12 t 0 equals t squared minus 4 t 0 equals t open parentheses t minus 4 close parentheses

t equals 0 or t equals 4

After t equals 0 the next point of rest is t equals 4

After t equals 0, it takes 4 seconds for the particle to come to rest

(d) Find the time at which the particle is decelerating at 3 ms-2.

A deceleration of 3 means an acceleration of -3
Differentiate the velocity function to find acceleration

a equals fraction numerator straight d v over denominator straight d t end fraction equals 6 t minus 12

Set a equals negative 3 and solve for t

6 t minus 12 equals negative 3 6 t equals 9 t equals 1.5

The particle is decelerating at 3 ms-2 at 1.5 seconds

Last updated:

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Flashcards

    Did this page help you?

    Previous:Problem Solving with DifferentiationNext:Basic Angle Properties
    Author
    Reviewer
    Mark Curtis

    Author: Mark Curtis

    Expertise: Maths

    Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.