Introduction to Sequences (Edexcel IGCSE Maths A (Modular)): Revision Note

Introduction to sequences

What are sequences?

• A sequence is an ordered set of numbers that follow a rule

  • For example 3, 6, 9, 12...

    • The rule is to add 3 each time

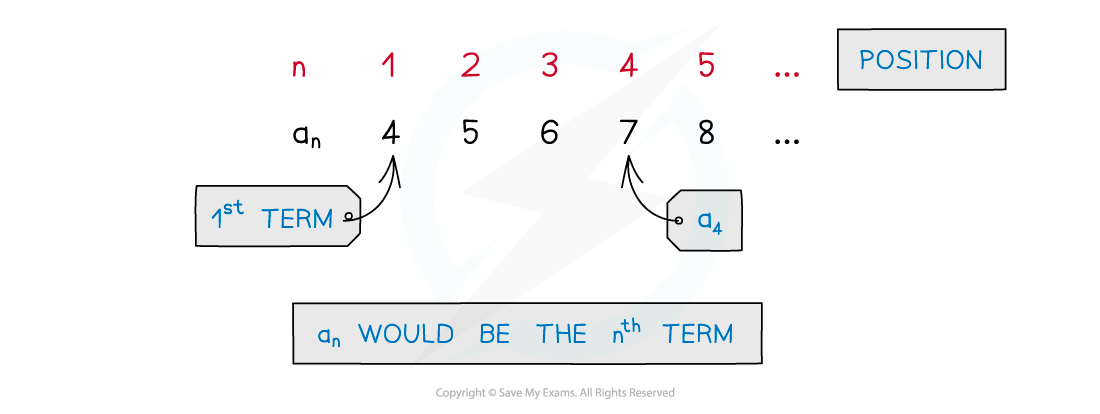
• Each number in a sequence is called a term

• The location of a term within a sequence is called its position

  • The letter n  is used for position

    • n  = 1 refers to the 1st term

    • n  = 2 refers to the 2nd term

    • If you do not know its position, you can say the n th term

• Another way to show the position of a term is using subscripts

  • A general sequence is given by a₁, a₂, a₃, ...

    • a₁ represents the 1st term

    • a₂ represents the 2nd term

    • a_n represents the nth term

How do I write out a sequence using a term-to-term rule?

• Term-to-term rules tell you how to get the next term from the term you are on

  • It is what you do each time

  • For example, starting on 4, add 10 each time

    • 4, 14, 24, 34, ...

How do I write out a sequence using a position-to-term rule?

• A position-to-term rule is an algebraic expression in n  that lets you find any term in the sequence

  • This is also called the n th term formula

• You need to know what position in the sequence you are looking for

  • To get the 1st term, substitute in n  = 1

  • To get the 2nd term, substitute in n  = 2

• You can jump straight to the 100th term by substituting in n  = 100

  • You do not need to find all 99 previous terms

• For example, the n th term is 8n  + 2

  • The 1st term is 8×1 + 2 = 10

  • The 2nd term is 8×2 + 2 = 18

  • The 100th term is 8×100 + 2 = 802

How do I know if a value belongs to a sequence?

• If you know the n th term formula, set the value equal to the formula

  • This creates an equation to solve for n

• For example, a sequence has the n th term formula 8n  + 2

  • Is 98 in the sequence?
    
    

    • It is in the sequence, it is the 12th term

  • Is 124 in the sequence?
    

    • n  is not a whole number, so it is not in the sequence